Признак параллельности прямой и плоскости
Теорема
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Доказательство
Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.
| ||
Вопрос №10
Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.
Таким образом, задать функцию, значит задать три объекта:
1) множество Х (область определения функции);
2) множество Y (область значений функции);
3) правило соответствия f (сама функция).
Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x3. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу fсоответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x3 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x3 принимает значение у= f(2) =23 =8.
Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x2.
Графический способ. Графиком функции y=f(x)называется множество всех точек плоскости с координатами (x, f(x)). График содержит всю информацию о функции. Имея перед собой график, мы как бы "видим функцию".
Табличный способ. Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х.
Сложная функция –функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).
Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:
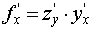 .
.
Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f1(y1),y1 = f2(y2), …, yn-1 = fn(x), то
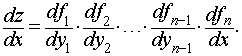
Функция 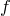 называется обратимой, если для любых двух различных чисел
называется обратимой, если для любых двух различных чисел 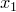 и
и 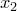 , принадлежащих
, принадлежащих 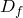 , числа
, числа 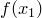 и
и 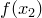 также различны.
также различны.
Строго монотонная функция обратима.
Функция является обратимой в том и только в том случае, если любая прямая, перпендикулярная оси ординат, имеет с ее графиком не более одной общей точки.
Пусть функция 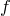 обратима,
обратима, 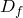 — ее область определения,
— ее область определения, 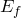 — множество ее значений. Для каждого числа
— множество ее значений. Для каждого числа 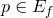 обозначим через
обозначим через 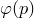 такое число
такое число 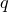 из множества
из множества 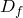 , что
, что 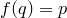 (такое число существует и притом только одно). Мы получили новую функцию с областью определения
(такое число существует и притом только одно). Мы получили новую функцию с областью определения 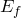 и множеством значений
и множеством значений 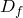 . Эта функция называется обратной функции
. Эта функция называется обратной функции 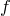 .
.
Графики взаимно обратных функций в одной и той же координатной плоскости симметричны относительно биссектрисы первой и третьей четверти.
Пусть функция 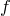 с областью определения
с областью определения 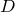 и множеством значений
и множеством значений 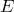 имеет обратную функцию
имеет обратную функцию 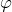 . Пусть
. Пусть 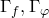 — графики функций
— графики функций 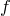 и
и 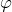 соответственно. Точка
соответственно. Точка 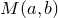 принадлежит
принадлежит 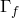
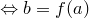
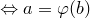
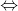 точка
точка 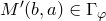 . Осталось доказать, что точки
. Осталось доказать, что точки 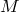 и
и 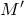 симметричны относительно биссектрисы первой и третьей четверти. Эта биссектриса состоит из точек
симметричны относительно биссектрисы первой и третьей четверти. Эта биссектриса состоит из точек 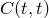 , где
, где 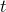 — любое вещественное число. Чтобы доказать, что точки
— любое вещественное число. Чтобы доказать, что точки 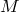 и
и 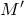 симметричны относительно биссектрисы, достаточно проверить, что биссектриса является серединным перпендикуляром отрезка
симметричны относительно биссектрисы, достаточно проверить, что биссектриса является серединным перпендикуляром отрезка 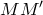 , то есть что любая точка
, то есть что любая точка 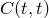 равноудалена от точек
равноудалена от точек 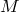 и
и 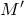 .
.
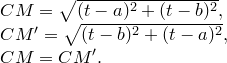
Основные элементарные функции
Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол 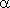 , тангенскоторого равен k : tan
, тангенскоторого равен k : tan 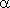 = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом.
= k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом.
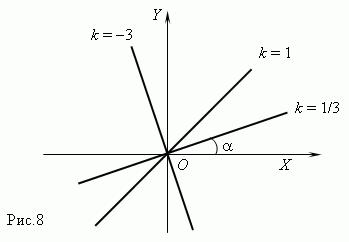
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет.
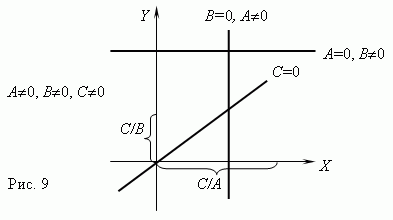
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина.
Квадратичная функция. Это функция:y = ax 2 + bx + c, где a, b, c - постоянные, a  0. В простейшем случае имеем: b = c = 0 и y =ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет осьсимметрии OY, которая называется осью параболы.Точка O пересечения параболы с её осью называется вершиной параболы. График функцииy = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в началекоординат, а в точке с координатами:
0. В простейшем случае имеем: b = c = 0 и y =ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет осьсимметрии OY, которая называется осью параболы.Точка O пересечения параболы с её осью называется вершиной параболы. График функцииy = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в началекоординат, а в точке с координатами:
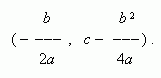
Степенная функция. Это функция:y = axn, где a , n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n= 2 - квадратную параболу; при n = -1 - обратную пропорциональность или гиперболу.Таким образом, эти функции - частныеслучаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, при n = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:
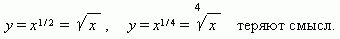
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией.Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию.
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называетсялогарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла. Основные характеристики и свойства логарифмической функции:
- область определения функции: x > 0,а область значений: -  < y < +
< y < + 
( т.e. y 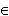 R );
R );
- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.
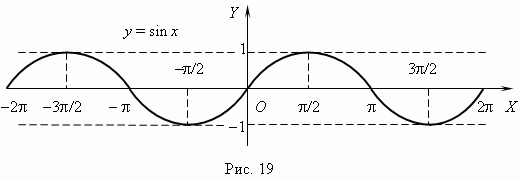
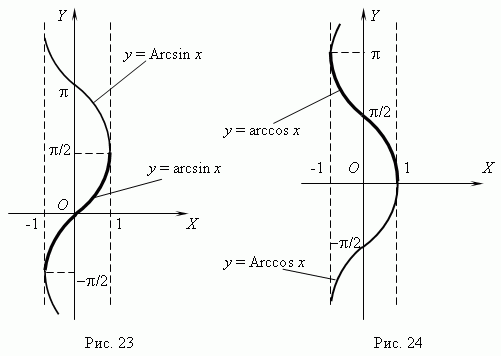
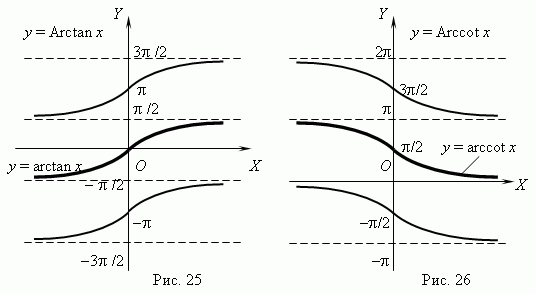
Обратные тригонометрические функции. Функции y = Arcsin x ( рис.23 ) и y = Arccos x ( рис.24 )многозначные, неограниченные; их область определения и область значений соответственно: -1 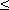 x
x 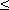 +1 и -
+1 и - 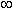 < y < +
< y < + 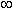 . Поскольку эти функции многозначные, не
. Поскольку эти функции многозначные, не
рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
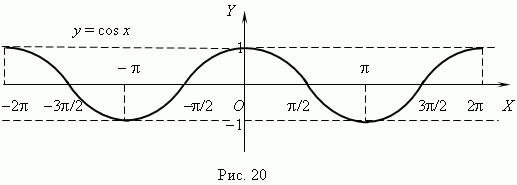
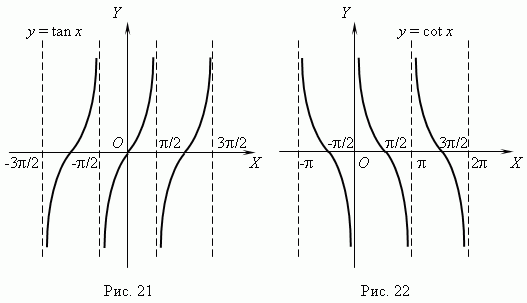
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 )- многозначные, неограниченные функции; их область определения: - 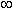
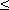 x
x 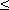 +
+ 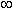 . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
. Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение
x2 + y2 - 1 = 0
задаёт Неявные функции
y = у (х),
Неявные функции могут быть как однозначными, так и многозначными. Не всякое соотношение (или система соотношений) между переменными задаёт Неявные функции Так, если ограничиваться лишь действительными значениями переменных, то соотношение x2 + y2 + 1 = 0 не задаёт Неявные функции, так как не удовлетворяется ни одной парой действительных значений х и у; соотношение же exy = 0 вообще не удовлетворяется ни одной парой действительных или комплексных значений х и у. Теорема существования Неявные функции в её простейшей формулировке утверждает, что если функция F (x, y)обращается в нуль при паре значений х = x0, у = y0 [F (x0, y0) ¹ 0] и дифференцируема в окрестности точки (x0, y0), причём F’x (х, у) и F’y (х, у) непрерывны в этой окрестности и F’y (x0, y0) ¹ 0, то в достаточно малой окрестности точки x0 существует одна и только одна однозначная непрерывная функция у = у (х),удовлетворяющая соотношению F (x, y) = 0 и обращающаяся в y0 при x = x0; при этом y"(x) = —F’x (x, y)/F’y (x, у).
До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений
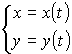
где t - вспомогательная переменная, называемая параметром.
Заметим, что функция может быть представлена в параметрической форме различными способами.
Например, функция, записанная в неявном виде x2 + y2 = 1 может быть представлена в явном виде: 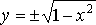 и в параметрической форм е:
и в параметрической форм е:
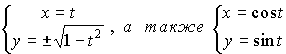
Вопрос №11
Предел функции
Пусть функция игрик равно ф от икс определяется в некоторой окретсности С>0 те дана точка Х0, она опреденеа в некотором интервале, неограниченно стретемиться к точке х0, Фунция определена в окрестности Х0 но не обязательно определна в самой точке Х0. Будем говорить что х стремиться к Х0.
Число а называется пределом функции игрик равно ф от икс при х стремящимся к Х0 если для всех икс дсотаточно мало отличающихся от х нулевого существует значение функции ф от икс, сколько угодно мало отличающегося от числа а.
Односторонние пределы
Число бэта называется правым пределом/левым пределом фунцкии в точке а если для любого положительного Е существует положительное гамма >0 такое что для любых значений икс, удовлетворяющих условию, справедливо неравество.
Для того чтобы функция имела предела в точке а необходимо и достаточно чтобы правый и левый пределы существовали в этой точке.
Предел функции в бесконечности
Пусть функция f(x) определена на (a, + ∞).
Число A называется пределом функции f(x) при x → + ∞ (обозначается A =
| lim |
| x → + ∞ |
f(x) ), если
| " ε > 0 $ N: " x > N Ю |f(x) − a| < ε. |
Пусть функция f(x) определена на ( − ∞,a).
Число A называется пределом функции f(x) при x → − ∞ (обозначается A =
| lim |
| x → − ∞ |
f(x) }, если
| " ε > 0 $ N: " x < − N Ю |f(x) − a| < ε. |
Если существуют пределы функции f(x) при x → + ∞ и при x → − ∞ и они равны одному и тому же числу A, то это число A называется пределом функции f(x) при x→ ∞ {обозначается
A =
| lim |
| x → ∞ |
f(x) .
Теоремы о пределах последовательностей и правила их вычисления распространяются и на пределы функций в бесконечности.
Бесконечные пределы Определение 2.13 Пусть функция 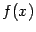 определена на некотором окончании
определена на некотором окончании  базы
базы  и имеет следующее свойство:
и имеет следующее свойство:
для любого, как угодно большого, положительного числа  можно найти такое окончание
можно найти такое окончание  базы
базы  , что при любом
, что при любом  будет выполнено неравенство
будет выполнено неравенство
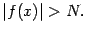
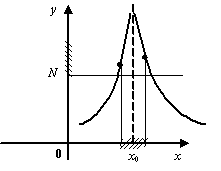
Рис.2.29.Бесконечно большая при базе 
Тогда функция 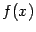 называется бесконечно большой при базе
называется бесконечно большой при базе  ; это обозначается так:
; это обозначается так:
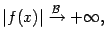
или так:
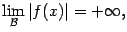
или даже так:
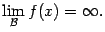
Если при этом 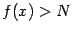 при
при  , то для положительной бесконечно большой
, то для положительной бесконечно большой 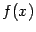 можно писать
можно писать 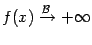 или
или 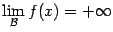 , а если
, а если 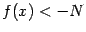 , то для отрицательной бесконечно большой
, то для отрицательной бесконечно большой 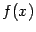 можно писать
можно писать 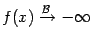 или
или 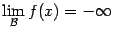 .
.
Нужно, конечно, чётко осознавать, что предел, равный бесконечности, -- это чисто условная запись и что в этом случае никакого числового значения такой предел не имеет и, следовательно, не существует, в смысле определения предела функции.
Пример 2.24 Примером бесконечно большой при 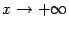 может служить
может служить 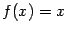 : в качестве окончания
: в качестве окончания  можно тогда взять
можно тогда взять 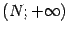 . Очевидно, что тогда
. Очевидно, что тогда 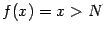 , если
, если  .
.
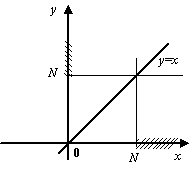
Рис.2.30.График 
Пример 2.25 Примером положительной бесконечно большой при 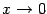 может служить
может служить 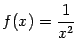 .
.
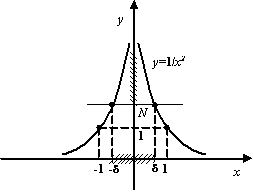
Рис.2.31.График 
В качестве упражнения найдите зависимость числа 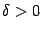 , задающего окончание
, задающего окончание 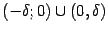 базы
базы 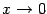 , от числа
, от числа 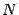 .
.
Пример 2.26 Примером отрицательной бесконечно большой при 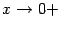 может служить функция
может служить функция 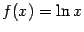 .
.
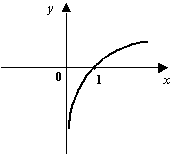
Рис.2.32.График 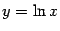
В качестве упражнения найдите зависимость числа  , задающего окончание
, задающего окончание 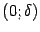 базы
базы 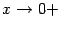 , от числа
, от числа 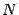 .
.
Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.
Теорема 2.16 Пусть 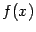 -- функция, бесконечно большая при базе
-- функция, бесконечно большая при базе  . Тогда величина
. Тогда величина 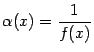 -- бесконечно малая при базе
-- бесконечно малая при базе  .
.
Доказательство. Для начала заметим, что на всех достаточно далёких окончаниях 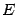 базы
базы  будет
будет 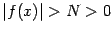 , так что функция
, так что функция 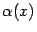 определена на этих окончаниях. Далее, пусть взято некоторое
определена на этих окончаниях. Далее, пусть взято некоторое  . Положим
. Положим 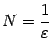 и выберем такое окончание
и выберем такое окончание 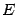 , что
, что 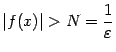 при
при 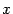 из этого окончания. Тогда
из этого окончания. Тогда  при таких
при таких 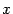 , что и означает, что
, что и означает, что  .
.
Замечание 2.9 Утверждение, обратное к доказанной теореме, вообще говоря, неверно: если 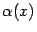 -- бесконечно малая при базе
-- бесконечно малая при базе  , то функция
, то функция 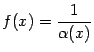 не всегда является бесконечно большой при базе
не всегда является бесконечно большой при базе  , хотя бы потому, что может быть не определена ни на каком окончании
, хотя бы потому, что может быть не определена ни на каком окончании 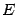 базы
базы  . Простейший пример -- это постоянная величина
. Простейший пример -- это постоянная величина 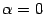 , которая, очевидно, бесконечно мала при любой базе (
, которая, очевидно, бесконечно мала при любой базе ( 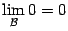 ), но
), но 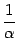 не имеет смысла ни при каких
не имеет смысла ни при каких 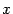 . Однако если сделать дополнительное предположение, что
. Однако если сделать дополнительное предположение, что  при всех
при всех 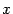 из некоторого окончания
из некоторого окончания 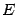 базы
базы  , то обратное утверждение становится верным.
, то обратное утверждение становится верным.
Теорема 2.17 Пусть 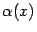 -- такая бесконечно малая при базе
-- такая бесконечно малая при базе  , что
, что  при всех
при всех 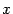 из некоторого окончания базы
из некоторого окончания базы  . Тогда функция
. Тогда функция 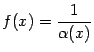 -- бесконечно большая при базе
-- бесконечно большая при базе  .
.
Докажите эту теорему в качестве упражнения.
Утверждение, что некоторая функция 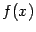 является бесконечно большой положительной величиной при базе
является бесконечно большой положительной величиной при базе  означает при вычислении пределов, что при замене
означает при вычислении пределов, что при замене 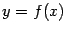 база
база  переходит в базу
переходит в базу 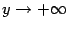 . Если же
. Если же 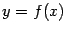 -- отрицательная бесконечно большая, то после замены получится база
-- отрицательная бесконечно большая, то после замены получится база 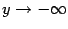 . Прослеживая за изменениями баз при последовательных заменах, можно вычислять многие пределы.
. Прослеживая за изменениями баз при последовательных заменах, можно вычислять многие пределы.
Пример 2.27 Найдём предел 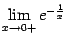 .
.
Рассмотрим замену 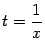 . При
. При 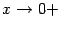 будет
будет 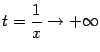 . Пусть теперь
. Пусть теперь 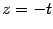 . При
. При 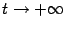 будет
будет 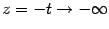 . Наконец, пусть
. Наконец, пусть 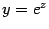 . При
. При 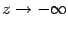 будет
будет 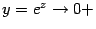 . (См. графики, расположенные ниже.) Последнее соотношение означает, что
. (См. графики, расположенные ниже.) Последнее соотношение означает, что

(и что, вдобавок, величина 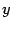 остаётся положительной).
остаётся положительной).
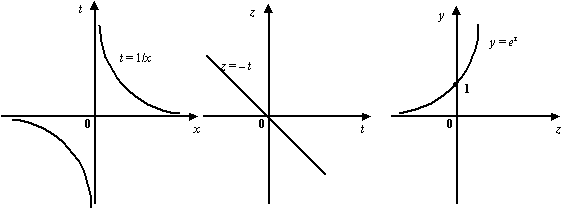
Рис.2.33.Графики зависимостей 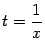 ,
, 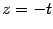 ,
, 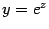
Заметим, что при решении было важно отследить изменение функций именно при 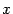 , стремящемся к 0 справа. В качестве упражнения покажите, что если бы рассматривалась база
, стремящемся к 0 справа. В качестве упражнения покажите, что если бы рассматривалась база 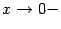 , то получилась бы бесконечно большая положительная величина
, то получилась бы бесконечно большая положительная величина  , а при базе
, а при базе 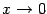 величина
величина 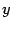 не имеет никакого предела и не является бесконечно большой.
не имеет никакого предела и не является бесконечно большой.
Свойства пределов
1) если предел фунцкии при х стремящимся к а равен А где А конечное число то на некоторой окрестности У (а) функция ф от икс ограничена те существует положительное число М такое что |f(x)|<=M для всех икс принадлежащих У(а) икс не равно а.
2) Если предел функции равен А и Анеравно 0 и является конечным числом то существует окрестность У(а) такая что |f(x)|>|A|/2 х не равен а, и принадлежит Y(a)
3) Если предел f1(x) равен А1, а предел f2(x) равен А2 и н7а некоторой окрестности У(а) х не равен а, а f1(x) <= f2(x) то А1<=A2.
4) Если …. F1(x) <= фи (x) <=f2(x) то предел фи (х) при х стремящимся к а, равен А.
5) Критерий каши существование предела
Для тогоч тчобы сщуестовал конечный предел, необходимо и достаточно чтобы функция f(x) ыла определана в окрестности а, за исключением быть может самой точки а и для эпсилон больше 0, существовала окрестности Y(a) что, каковы бы не были точки х штрих х н принадлежащие У(а) х штрих и х н не равны а. |f(x)штрих-f(x)n | < епсилон.
Теорема о переходе к пределу в неравенстве
Пусть 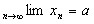 и
и 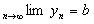 ;
; 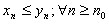 ,Тогда
,Тогда 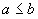 Док-во: предложим противное:
Док-во: предложим противное: 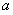 >
>  <
< 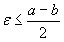 ;по определению пределов:
;по определению пределов:
(*) 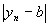 <
< 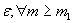
(**) 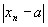 <
< 
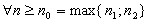 будут выполнены (*) и (**)
будут выполнены (*) и (**)
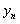 <
< 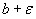 <
< 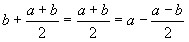 <
< 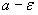 <
< 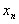 ;т.е
;т.е
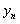 <
< 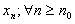 ,что противоречит условию значит
,что противоречит условию значит 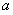 <
<  не верно,а
не верно,а 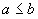 -верно(утверждение теоремы);
-верно(утверждение теоремы);
если в условии теоремы записать,что 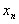 <
< 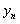 ;
; 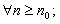 то
то 
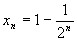 <
< 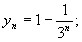
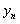 >
> 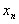
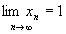 =
= 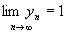
Теорема о переходе к пределу в равенстве
Если 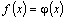 на
на  и существует
и существует 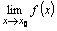 , то существует
, то существует 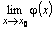 и
и 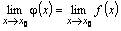 .
.
ПРИМЕР. Поскольку 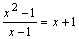 для
для 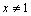 и
и 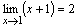 , то
, то 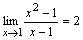 .
.
Непрерывность в точке
Пусть дана фунция она определена в точке Х0 и в ее окрестностях, обозначим х-х0 как дельта Х.
Приращение функции дельта у, называют дельта у=f(x+Х0)-f(X0)
Функция называет непрерывной в точке Х0 если бесконечно малому дельта х соотвествует бесконечно малое дельта у.
Функция неприрывна в точек Х0, если предел функции при х стремящимся к 0 равен функйции от Х0.
Если функция f1(x) f2(x) непрерывны в точке х0 то неприрывны в этой точке суммы и разность f1)x) f2(x) , произведение f1(x)*f2(x) и их частное, Если f2(x) не равно 0.
Если функция U=фи(х) непрерывна в точке Х0 а для у=f(U) непрерывна в точке U0 равно фи (Х0) то сложная функция y=f(U) равен фи(x) непрерывна в точке Х0.
Функция непрерывна в точке а, если бесконечно малое и бесконечно большое= f(a)
Вопрос №13
Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?
Определения. Пусть при 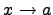 функции f(x) и g(x) являются бесконечно малыми. Тогда:
функции f(x) и g(x) являются бесконечно малыми. Тогда:
2. Если  , то f(x) называется бесконечно малой высшего порядка относительно g(x).
, то f(x) называется бесконечно малой высшего порядка относительно g(x).
2. Если  (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).
(конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).
3. Если  , то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так:
, то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так: 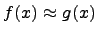 .
.
Свойства эквивалентных бесконечно малых:
1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.
2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.
Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак 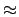 мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.
мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.
Эквиваленты
| sinα(x)~α(x) | |
| arcsinα(x)~α(x) | |
| tgα(x)~α(x) | |
| arctgα(x)~α(x) | |
| loga(1+α(x))~(logae)α(x) | |
| ln(1+α(x))~α(x) | |
| aα(x)-1~α(x)lna,a>0,a≠1 | |
| eα(x)-1~α(x) | |
| (1+α(x))μ-1~μα(x) | |
| 1+α(x)n-1~α(x)n | |
| 1+α(x)-1~α(x)2 | |
| 1-cosα(x)~12α2(x) |
БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ
Расстановка ударений: БЕСКОНЕ`ЧНО БОЛЬША`Я ФУ`НКЦИЯ
БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:

Аналогичным образом определяются
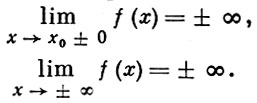
Напр.,
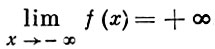
означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) является бесконечно малой.
Связь между бесконечно малыми и бесконечно большими функциями
Если f(x) — бесконечно большая функция при x → x0, то
| f(x) |
— бесконечно малая функция при x → x0.
Если α(x) — бесконечно малая функция при x → x0 и "x О
| · |
| O |
(x0) α(x) ≠ 0, то
| α(x) |
— бесконечно большая функция при x → x0.
Вопрос №14
Непрерывность функции на отрезке
Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.
Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.
Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
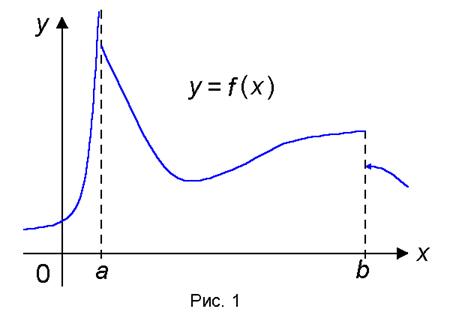
Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)
Множество функций, непрерывных на отрезке [a, b] обозначается символ

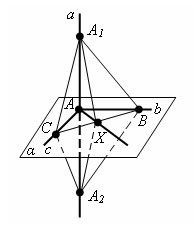 Доказательство Пусть a – прямая, перпендикулярная прямым b и с в плоскости α. Тогда прямая a проходит через точку A пересечения прямых b и с. Докажем, что прямая a перпендикулярна плоскости α. Проведем произвольную прямую x через точку A в плоскости α и покажем, что она перпендикулярна прямой a. Проведем в плоскости α произвольную прямую, не проходящую через точку A и пересекающую прямые b, с и x. Пусть точками пересечения будут B, C и X. . Отложим на прямой a от точки A в разные стороны равные отрезки AA1 и AA2. Треугольник A1CA2 равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению. Треугольник A1BA2 так же равнобедренный. Следовательно, Δ A1BC = ΔA2BC по третьему признаку равенства треугольников. Из равенства треугольников A1BC и A2BC следует равенство углов A1BX и A2BX, следовательно, равенство треугольников A1BX и A2BX по первому признаку равенства треугольников. Из равенства сторон A1X и A2X, следует, что A1XA2 равнобедренный. Поэтому его медиана XA является высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости α. Теорема доказана.
Доказательство Пусть a – прямая, перпендикулярная прямым b и с в плоскости α. Тогда прямая a проходит через точку A пересечения прямых b и с. Докажем, что прямая a перпендикулярна плоскости α. Проведем произвольную прямую x через точку A в плоскости α и покажем, что она перпендикулярна прямой a. Проведем в плоскости α произвольную прямую, не проходящую через точку A и пересекающую прямые b, с и x. Пусть точками пересечения будут B, C и X. . Отложим на прямой a от точки A в разные стороны равные отрезки AA1 и AA2. Треугольник A1CA2 равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению. Треугольник A1BA2 так же равнобедренный. Следовательно, Δ A1BC = ΔA2BC по третьему признаку равенства треугольников. Из равенства треугольников A1BC и A2BC следует равенство углов A1BX и A2BX, следовательно, равенство треугольников A1BX и A2BX по первому признаку равенства треугольников. Из равенства сторон A1X и A2X, следует, что A1XA2 равнобедренный. Поэтому его медиана XA является высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости α. Теорема доказана.