Тройной интеграл и его вычисление.

По аналогии с двойным интегралом вводится понятие тройного интеграла.

Рассмотрим ограниченную замкнутую пространственную область V и определённую в ней непрерывную функцию . Аналогично строится интегральная сумма по данному объёму и определяется тройной интеграл от функции по пространственной области V:

=

или

= .

Тройной интеграл обладает свойствами, аналогичными свойствами двойного интеграла.

Предположим, что область V является стандартной в направлении оси , т.е. удовлетворяет следующим условиям:

1) всякая прямая, параллельная оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках;

2) проекция S области V на плоскость представляет собой стандартную область в направлении оси 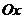или оси .

Если стандартная область V ограничена сверху поверхностью , снизу ─ поверхностью , а проекция S области V стандартна в направлении оси и определяется неравенствами , , то

= .

Замечание 1.Если область S является стандартной в направлении оси 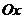и определяется неравенствами , , то

= .

Замечание 2.Если область V является стандартной в направлении каждой координатной оси и её проекции на координатные плоскости являются стандартными в направлении каждой соответствующей оси, то пределы интегрирования в трёхкратном интеграле можно расставить шестью различными способами.

Замечание 3.Если V ─ прямоугольный параллелепипед, определяемый неравенствами , , , то

= .

Основные понятия.

Пусть дана бесконечная последовательность чисел . Символ

обозначаемый 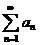, называется числовым рядомили просто рядом,а числа - членамичислового ряда. Суммы конечного числа членов ряда , …, называются частными суммами(или отрезками) числового ряда. Рассмотрим последовательность . Если существует предел 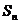, то числовой ряд 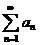называется сходящимся,а число - суммойэтого ряда. В этом случае пишут

= = .

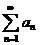Если же последовательность не имеет предела, то ряд называется расходящимся. Такой ряд суммы не имеет.

Основные свойства числовых рядов.

2.1.Если в ряде 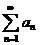= отбросить конечное число первых членов, то получим ряд

,

который называется -ымостаткомданного ряда.

-ый остаток данного ряда сходится (или расходится) одновременно с данным рядом. Это означает, что при исследовании ряда на сходимость можно игнорировать конечное число его первых членов.

2.2.Необходимый признак сходимости ряда:

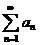общий член сходящегося ряда стремится к нулю при , т.е. = 0. Это означает, что если ¹ 0, то ряд 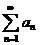расходится.

2.3.Если ряд 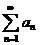сходится и его сумма равна , то ряд , где произвольное число, также сходится и его сумма равна .

2.4.Если ряды 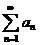и сходятся и их суммы соответственно равны и , то ряд также сходится и его сумма .

Положительные ряды.

Положительным рядомназывается ряд, члены которого неотрицательны.

1) Признак сравнения рядов.Пусть даны два положительных ряда

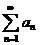= (1)

= (2)

Если выполняется условие , то из сходимости ряда (2) следует сходимость ряда, а из расходимости ряда (1) следует расходимость ряда (2).

2) Признак Даламбера. Если члены положительного ряда 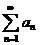таковы, что существует предел , то при ряд расходится, а при сходится.

3) Интегральный признак Коши.Пусть члены положительного ряда 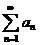такие, что где функция 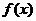при непрерывна, положительна убывает. Тогда данный ряд и несобственный интеграл

сходится или расходится одновременно.

Знакочередующиеся ряды.

Определение. Знакочередующимся рядомназывается ряд вида

(1)

где

1) признак Лейбница. Если члены знакочередующегося ряда (1) удовлетворяют условиям а) ;

б) 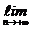= 0,

то знакочередующийся ряд сходится.