Понятие функции нескольких переменных.

Рассмотрим арифметическое n-мерное пространство.

Rⁿ = {(x₁,x₂,…,x_n)│x₁,x₂,…,x_n ÎR}.

Пусть Х ─ подмножество элементов множества Rⁿ и Y ─ некоторое множество элементов у. Если каждому элементу (x₁,x₂,…,x_n)ÎХ поставлен в соответствие единственный элемент уÎΥ, то говорят на множестве Х задана функция у = f(x₁,…x_n) со значениями в множестве Y.Такая функция называется функцией n переменныхx₁,x₂,…,x_n.

В частности, при n = 2 имеем функцию двух аргументов у = f(x₁,x₂) или z = f(x;y). При n = 3 получаем функцию трёх переменных у = f(x₁,x₂,x₃) или u = f(x;y;z).

Предел функции.

Рассмотрим функцию у = f(x), определённую в некотором интервале, содержащем точку х = а.

Определение.Число А называется пределом функцииу = f(x) при х, стремящемся к a (или в точке а),если для любого числа e>0 существует такое d>0, что при всех х, удовлетворяющих условию

0 < │х − а│< d, (1)

выполняется неравенство

│f(x) − A│< e. (2)

Обозначения предела функции f(x) при х, стремящемся к а:

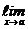f(x) = A;

f(x) → A при х → а.

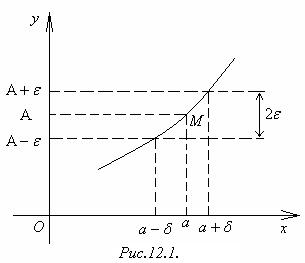
Выясним геометрический смысл этого определения, воспользовавшись, графиком функции у = f(x) (рис.12.1). Неравенство (1) означает, что х отстоит от точки а не далее, чем на d, т.е. принадлежит интервалу (а − d; а + d). Неравенство (2) означает, что значения функции у = а(ч) не выходят из интервала (А − e; А + e) оси Оу. Следовательно, точки М графика функции у = f(x) должны находится в полоске шириной 2e, ограниченной прямыми у = А − e, у = А + e для всех значений х, удалённых от точки а не далее, чем на d.

Односторонние пределы функции.

Определение.Число А называется правым (левым) пределом функции f(x) в точке а,если для любого e > 0 существует d > 0 такое, что для всех х, удовлетворяющих неравенствам а < x < a + d (a −d < x < a), выполняется неравенство │f(x) − A│< e. Обозначение 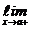f(x) = A ( 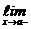f(x) = A).

Связь между односторонними пределами и пределом функции устанавливает следующая теорема.

Теорема 1. Функция у = f(x) имеет в точке а предел тогда и только тогда, когда в этой точке существует как левый, так и правый предел и они равны. В этом случае предел функции равен односторонним пределам.

Доказательство.

1) Пусть 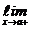f(x) = 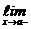f(x) = A. Тогда по определению односторонних пределов, для любого e>0 существуют числа d₁>0 и d₂>0 такие, что для всех х, удовлетворяющих неравенствам а<x<a+d₁, a−d₂< x < a, выполняется неравенство │f(x)−A│<e. Возьмём d = min{d₁,d₂}. Тогда для всех х, удовлетворяющих неравенствам а−d<x<a+d(или 0<│х−а│<d) выполняется неравенство │f(x)−A│<e. Это означает, что 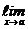f(x) = A.

2) Пусть теперь 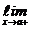f(x) = A. Тогда по определению, для любого e>0 существует число d>0 такое, что для всех х, удовлетворяющих неравенствам 0 <│х − а│< d, выполняется неравенство │f(x)−A│<e. Следовательно, для e>0 существует d>0 такое, что для всех х, удовлетворяющих неравенствам а<x <a+d, (или a−d < x <a), выполняется неравенство │f(x)−A│<e. Это означает, что существует односторонние пределы 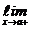f(x) и 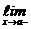f(x), причём оба они равны числу А.