Поверхности вращение второго порядка.

Определение. Поверхностью вращения второго порядканазывается поверхность, образованная вращением линии второго порядка её оси.

1) Эллипсоид вращения.При вращении эллипса 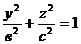, х = 0 вокруг оси Оz

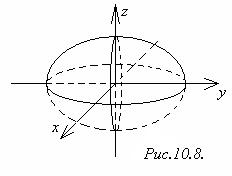
получим поверхность, которая называется

эллипсоидом вращения. 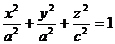(рис.10.8).

При а = с получаем сферу х² + у² + z² = a².

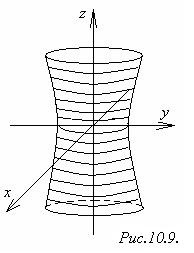2) Однополостный гиперболоидобразуется при вращении гиперболы ,

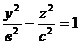х = 0 вокруг оси Оz.

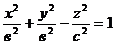(рис.10.9).

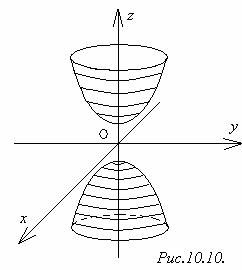3) Двуполостный гиперболоидобразуется при вращении гиперболы 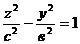, х = 0 вокруг оси Оz.

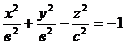(рис.10.10).

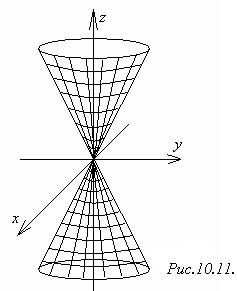4) Конус вращенияобразуется при вращении прямых 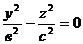, х = 0 вокруг оси Оz.

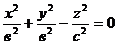(рис.10.11).

5) Параболоид вращенияполучается вращением параболы у² = 2рz , х = 0 вокруг оси Оz

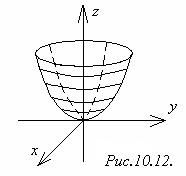х² + у² = 2рz или 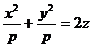(рис.10.12).

Поверхности второго порядка.

1) Трёхосный эллипсоид(рис.10.13)

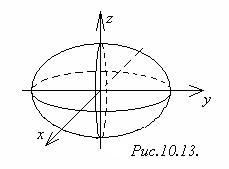
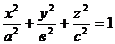
2) Однополостный гиперболоид .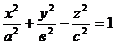

3) Двуполостный гиперболоид .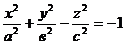

4) Конус второго порядка .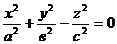

5) Эллиптический параболоид .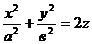

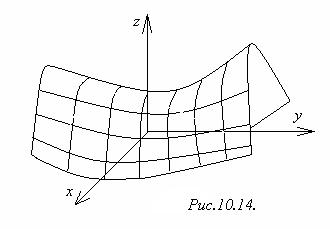6) Гиперболический параболоид 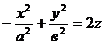(рис.10.14).

Линейные пространства и их простейшие свойства.

Определение.Рассмотрим непустое множество V и множество действительных чисел R. Определим операцию сложения элементов множества V (её называют внутренней операцией): любой упорядоченной паре элементов х,у Î V поставим в соответствие третий элемент z Î V, называемый их суммой; будем писать в этом случае z = x + y. Введём также операцию умножения элементов множества V на действительные числа (эту операцию называют внешней): каждому элементу х Î V и действительному числу aÎ R поставим в соответствие элемент z = ax = xa Î V. Потребуем, чтобы операция сложения элементов множества V и операция умножения элементов V на действительные числа удовлетворяли следующим аксиомам:

1) Сложение коммутативно, т.е. х + у = у + х для любых х, у ÎV.

2) Сложение ассоциативно, т.е. х + (у + z) = (x + y) + z для любых х, у, z ÎV.

3) В V существует нулевой элемент,обозначим этот элемент символом О. Это такой элемент, который в сумме с любым элементом хÎV даёт тот же элемент х, т.е.

х + О = О + х = х.

4) Для каждого элемента хÎV существует противоположный элемент,т.е. такой элемент, который в сумме с данным даёт нулевой элемент; элемент, противоположный элементу х обозначим (-х), тогда х + (-х) = 0 для любого хÎV.

5) Для любого хÎV и числа 1ÎR верно равенство 1×х = х .

6) Для любых х, уÎV, a,bÎRверны равенства:

6.1) a(bх) = (ab)х,

6.2) a(х + у) = aх + aу,

6.3) (a + b)х = aх + bх.

Непустое множество V, в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие аксиомам 1) – 6), называется действительным линейным пространствомили действительным векторным пространством.Элементы такого пространства называютвекторами.

Примеры линейных пространств.

1) Действительным векторным пространством является множество всех векторов трёхмерного пространства, т.е. { 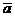= (а₁, а₂, а₃) ôа₁,а₂,а₃ ÎR}. Обозначается это пространство R³. Аналогично можно рассмотреть действительное линейное пространство R².

2)n-мерным арифметическим пространствомназывается действительное линейное пространство Rⁿ = {(а₁,а₂,…,а_n) ôа₁,а₂,…,а_nÎR}, в котором сложение элементов и умножение элементов на действительные числа определяется следующим образом:

а)(а₁,а₂,…,а_n) + (b₁,b₂,…,b_n) = (a₁ + b₁,…,a_n + b_n),

б)a(а₁,…,а_n) = (aа₁, aа₂,…,aа_n)

3) Множество всех матриц размерности m×n с действительными элементами

образует действительное линейное пространство с операциями сложения матриц и

умножения матрицы на число.

4) Множество всех действительных чисел образует действительное линейное пространство.

Из определения действительного линейного пространства нетрудно получить следующие его простейшие свойства.

1). В линейном пространстве имеется единственный нулевой элемент:

Доказательство. Предположим, что в линейном пространстве V имеются, два нулевых элемента О₁ и О₂. Так как О₁ ─ нулевой элемент, то О₁ + О₂ = О₂. Так как О₂ ─ нулевой элемент, то О₁ + О₂ = О₁. Следовательно, О₁ = О₁ + О₂ = О₂.

2).Для любого элемента хÎV существует единственный противоположный элемент (-х).

Доказательство.Предположим, что х₁ и х₂ ─ противоположные элементы в V для элемента х. Тогда х + х₁ = 0 и х + х₂ = 0. Но ввиду этого имеем

х₁ = 0 + х₁ = х₁ + 0 = х₁ + (х + х₂) = (х₁ + х) + х₂ = (х + х₁) + х₂ = 0 + х₂ = х₂.

3).Для любого элемента хÎV произведение О×х = О₁, где слева ОÎR, а справа О₁ÎV.

Доказательство. Ох + О₁ = Ох + (х + (-х)) = (Ох + х) + (-х) = (О +1)х + (-х) = х + (-х) = О₁.

Итак, Ох + О₁ = О₁. Так как О₁ ─ нулевой элемент V, то Ох = О₁.

4). Для любого элемента хÎV (-1)×х = -х, где –х ─ противоположный элемент для х.

Доказательство. (-1) ×х + х = (-1 +1)х = Ох = О₁. Следовательно, (-1)х = -х.

5). Для любого числа aÎR произведение a×О₁ = О₁, где О₁ ─ нулевой элемент V.

Доказательство.a × О₁ = a(х + (-х)) = a(х + (-1)х) = aх + a(-1)х = aх + (-a)х = (a + (-a))х= = Ох = О₁.

6).Если aх = О₁ и a¹0, то х = О₁.

Доказательство.Пусть aх = О₁ и a¹0. Тогда 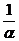(aх) = 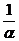×О₁ = О₁. Но 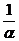(aх) = ( 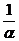×a)х = = 1х = х. Следовательно, х = О₁.

7).Если aх = 0 и х¹0, то a = 0.

Доказательство.Предположим, что a¹0. Тогда из свойства 6) имеем х = 0, что невозможно. Поэтому a = 0.