Длина вектора. Расстояние между точками в пространстве.

Пусть дан произвольны вектор =(х₀;у₀;z₀). Построим равный ему вектор ,начало которого совпадает с началом координат. Так как = ,то =(х₀;у₀;z₀).

Проведём через конец вектора плоскость, перпендикулярные осям (рис.8.13). Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок ОА. Из элементарной геометрии известно, что ОА² = .

Но ОА = , , , . Тогда из = 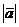имеем 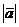² =х₀²+у₀²+z₀², откуда

(1)

Формула (1) выражает длину вектора через его координаты.

Пусть вектор = 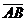, где А(х₁;у₁;z₁), В(х₂;у₂;z₂). По теореме 8.1.

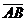=(х₂ – х₁; у₂ – у₁; z₂ – z₁). Из формулы (1)

│ │= .

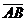Так как d ─ расстояние между точками А и В, равно │ 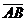│, то имеем формулу для нахождения расстояния между точками А и В

d = (2)

Деление отрезка в данном отношении.

Теорема 8.2.Пусть М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂). Если точка М(х₀;у₀;z₀) делит отрезок М₁М₂ в отношении α, то

, , (3)

Доказательство. Нетрудно заметить (рис.8.14), что = + . Так как , то = . Вектор = − .

Теперь,

= + ( − )×α,

+ ×α = + ×α,

×(1 + α) = + ×α,

= ( + ×α)× .

Перейдём к координатам: = (х₀;у₀;z₀), = (х₁;у₁;z₁), = (х₂;у₂;z₂). Тогда

(х₀;у₀;z₀) = ((х₁;у₁;z₁) + (х₂;у₂;z₂)α) × ,

откуда

, , .

Следствие.Пусть М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂). Если М₀(х₀;у₀;z₀) ─ середина отрезка М₁М₂, то

, , .

Разложение вектора по базисным векторам.

Пусть задана прямоугольная система координат в пространстве (рис.9.1). Введём в рассмотрение единичные векторы координатных осей Ох, Оу, Оz, соответственно. Вектор одинаково направлен с осью Оx, ─ с осью Оу, ─ с осью Оz. Векторы называются базисными векторами системы координат или ортами.

Пусть = (х₀,у₀,z₀) ─ произвольный вектор пространства. Отложим из начала координат О вектор = . По свойствам координат = (х₀,у₀,z₀). Пусть числу х₀ на оси Ох соответствует точка М_х, числу у₀ на Оу ─ М_у и числу z₀ на оси Оz ─ точка М_z. Тогда , , .

Так как ─ диагональ прямоугольного параллелепипеда, построенного на векторах , и , то нетрудно заметить, что

= + + ,

откуда

= = + + .

Последняя формула даёт разложение вектора по базисным векторам .

Скалярное произведение векторов.

Определение. Скалярным произведениемдвух векторов и называется число, равное произведению их модулей на косинус угла между векторами. Обозначение × .

Итак, по определению × = cosφ, где φ ─ угол между и .

Свойства скалярного произведения.

1. = × = cos0 = .

2. Свойство коммутативности: × = × .

Действительно, × = cosφ = × = cosφ.

3. Векторы и перпендикулярны тогда и только тогда, когда × = 0.

4. Косинус угла φ между векторами и вычисляется по формуле

cosφ = .

5. ×( α) = ( × )α , ( α)×( β) = ( × )(αβ).

6. ×( + ) = × + ×

Теорема 1.Если векторы = (х₁;у₁;z₁) и = (х₂;у₂;z₂), то × = х₁х₂ + у₁у₂ + z₁z₂.

Доказательство.Запишем разложение векторов и по базисным векторам :

= + + , = + +

Тогда, используя свойства скалярного произведения, имеем

× = ( + + )( + + ) ( )( ) + ( )( ) + ( )( ) +

+ ( )( ) + ( )( ) + ( )( ) + ( )( ) + ( )( ) + ( )( ) (х₁х₂) + ( )у₁х₂ + ( )z₁x₂ + ( )x₁y₂ + (y₁y₂) + ( )z₁y₂ + ( )x₁z₂ + ( )y₁z₂ + (z₁z₂)

Теперь, по свойству 1): = │ │ = 1, = 1, = 1.

По свойству 3): = = = = = = 0.

Следовательно,

× = х₁х₂ + у₁у₂ + z₁z₂.

Следствие 1.1.Если = (х₁;у₁;z₁) и = (х₂;у₂;z₂), то косинус угла между векторами и вычисляется по формуле

cosφ = .

Следствие 1.2.Векторы = (х₁;у₁;z₁) и = (х₂;у₂;z₂) перпендикулярны тогда и только тогда, когда х₁х₂ + у₁у₂ + z₁z₂ = 0.