Ступенчатая матрица. Ранг матрицы.
Определение. Ступенчатойбудем называть матрицу, которая обладает следующими свойствами:
1) если i-я строка нулевая, то (i + 1)-я строка также нулевая,
2) если первые ненулевые элементы i-й и (i + 1)-й строк расположены в столбцах с номерами k и R, соответственно, то k < R.
Условие 2) требует обязательного увеличения нулей слева при переходе от i-й строки к (i+ 1)-й строке. Например, матрицы
А1 = 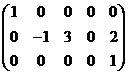 , А2 =
, А2 = 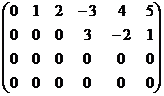 , А3 =
, А3 = 
являются ступенчатыми, а матрицы
В1 = 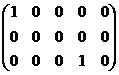 , В2 =
, В2 = 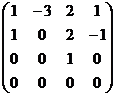 , В3 =
, В3 = 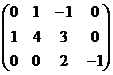
ступенчатыми не являются.
Теорема 5.1.Любую матрицу можно привести к ступенчатой с помощью элементарных преобразований строк.
Проиллюстрируем эту теорему на примере.
А= 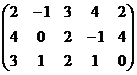
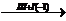
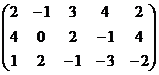
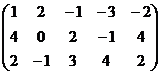
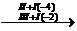
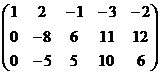
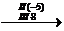
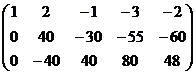
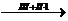

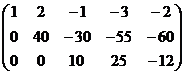 .
.
Получившаяся матрица ─ ступенчатая.
Определение. Рангом матрицыбудем называть число ненулевых строк в ступенчатом виде этой матрицы.
Например, ранг матрицы А в предыдущем примере равен 3.
Определители второго порядка.
Рассмотрим квадратную матрицу второго порядка
А = 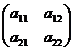 .
.
Определение. Определителем второго порядка,соответствующим матрице А,называется число, вычисляемое по формуле
│А│= 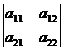 =
= 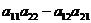 .
.
Элементы aij называются элементами определителя│А│, элементы а11, а22 образуют главную диагональ, а элементы а12, а21 ─ побочную.
Определители третьего порядка.
Рассмотрим квадратную матрицу третьего порядка
А = 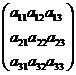 .
.
Определение. Определителем третьего порядка,соответствующим матрице А, называется число, вычисляемое по формуле
│А│= 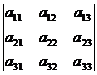 =
= 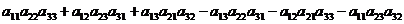 .
.
Чтобы запомнить, какие произведения в правой части равенства следует брать со знаком «плюс», а какие ─ со знаком «минус», полезно запомнить правило, называемое правилом треугольника:
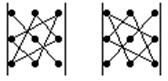

=─ .
Рассмотрим ещё один способ вычисления определителя третьего порядка.
Определение. Минором Mijэлементаaij определителя называется определитель, полученный из данного вычёркиванием i-й строки и j-го столбца. Алгебраическим дополнениемAij элемента aij определителя называется его минор Mij, взятый со знаком (-1)i+j.
Теорема 1. Определитель третьего порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
Док-во. По определению
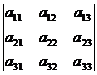 =
= 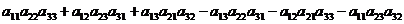 . (1)
. (1)
Выберем, например, вторую строку и найдём алгебраически дополнения А21, А22, А23:
А21 = (-1)2+1 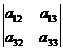 = -(
= -( 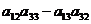 ) =
) = 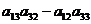 ,
,
А22 = (-1)2+2 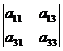 =
= 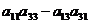 ,
,
А23 = (-1)2+3 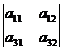 = - (
= - ( 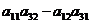 ) =
) = 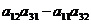 .
.
Преобразуем теперь формулу (1)
│А│= 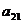 (
( 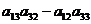 ) +
) + 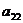 (
( 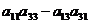 ) +
) + 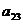 (
( 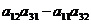 ) =
) = 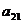 А21 +
А21 + 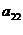 А22 +
А22 + 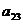 А23.
А23.
Формула
│А│= 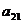 А21 +
А21 + 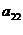 А22 +
А22 + 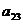 А23.
А23.
называется разложением определителя│А│ по элементам второй строки. Аналогично разложение можно получить по элементам других строк и любого столбца
6.3. Определитель n-го порядка (n Î N).
Определение. Определителем n-го порядка,соответствующим матрице n-го порядка
А = 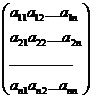
называется число, равное сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т.е.
│A│= 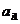 Аi1 +
Аi1 + 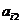 Ai2 + … +
Ai2 + … + 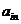 Ain =
Ain = 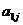 А1j +
А1j + 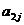 A2j + … +
A2j + … + 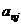 Anj
Anj
Нетрудно заметить, что при n = 2 получается формула для вычисления определителя второго порядка. Если n = 1, то по определению будем считать |A|=|a 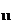 |=a
|=a 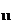 .
.
Свойства определителей.
Определение. Матрицу вида
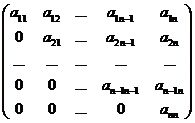
 или
или 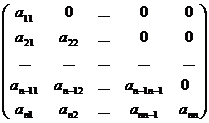
будем называть треугольной матрицей.
Свойство 1. Определитель треугольной матрицы равен произведению элементов главной диагонали, т.е.
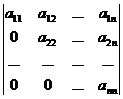 =
= 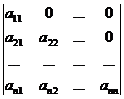 =
= 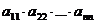 .
.
Свойство 2. Определитель матрицы с нулевой строкой или нулевым столбцом равен нулю.
Свойство 3.При транспонировании матрицы определитель не изменяется, т.е.
│А│= │Аt│.
Свойство 4.Если матрица В получается из матрицы А умножением каждого элемента некоторой строки на число k, то
│В│= k│А│.
Свойство 5.
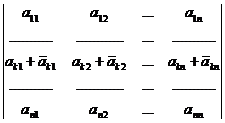 =
= 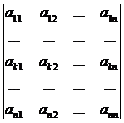 +
+ 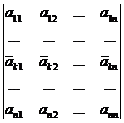 .
.
Свойство 6.Если матрица В получается из матрицы А перестановкой двух строк,
то│В│= −│А│.
Свойство 7.Определитель матрицы с пропорциональными строками равен нулю, в частности, нулю равен определитель матрицы с двумя одинаковыми строками.
Свойство 8.Определитель матрицы не изменяется, если к элементам одной строки прибавить элементы другой строки матрицы, умноженные на некоторое число.
Замечание. Так как по свойству 3 определитель матрицы не меняется при транспонировании, то все свойства о строках матрицы верны и для столбцов.
Свойство 9.Если А и В ─ квадратные матрицы порядка n, то │АВ│=│А││В│.
Обратная матрица.
Определение.Квадратная матрица А порядка n называется обратимой,если существует матрица В такая, что АВ = ВА = Еn. В этом случае матрица В называется обратной к матрицеА и обозначается А-1.
Теорема 2.Справедливы следующие утверждения:
1) если матрица А обратима, то существует точно одна ей обратная матрица;
2) обратимая матрица имеет определитель, отличный от нуля;
3) если А и В ─ обратимые матрицы порядка n, то матрица АВ обратима, причём (АВ)-1 =
= В-1 ×А-1.
Доказательство.
1) Пусть В и С ─ матрицы, обратные к матрице А, т.е. АВ = ВА = Еn и АС = СА = Еn. Тогда В = ВЕn = В(АС) = (ВА)С = ЕnС = С.
2) Пусть матрица А обратима. Тогда существует матрица А-1, ей обратная, причём
АА-1 = Еn.
По свойству 9 определителя │АА-1│=│А││А-1│. Тогда │А││А-1│=│Еn│, откуда
│А││А-1│= 1.
Следовательно, │А│¹ 0.
3) Действительно,
(АВ)(В-1А-1) = (А(ВВ-1))А-1 = (АЕn)А-1 = АА-1 = Еn.
(В-1А-1)(АВ) = (В-1(А-1А))В = (В-1Еn)В = В-1В = Еn.
Следовательно, АВ ─обратимая матрица, причём (АВ)-1 = В-1А-1.
Следующая теорема даёт критерий существования обратной матрицы и способ её вычисления.
Теорема 3. Квадратная матрица А обратима тогда и только тогда, когда её определитель отличен от нуля. Если │А│¹ 0, то
А-1 = 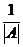
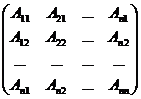 .
.
Систем линейных уравнений.
Совокупность уравнений вида
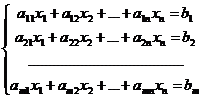 (1)
(1)
называется системой m линейных уравнений с n неизвестнымих1, х2,…, хn. Числа aij называются коэффициентами системы,а числа bi ─ свободными членами.
Решением системы (1)называется совокупность чисел с1, с2,…, сn, при подстановке которых в систему (1) вместо х1, х2,…,хn, получаем верные числовые равенства.
Решить систему ─ значит найти все её решения или доказать, что их нет. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений нет.
Матрица, составленная из коэффициентов системы
А = 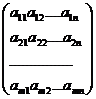
Называется матрицей системы (1). Если к матрице системы добавить столбец свободных членов, то получим матрицу
В = 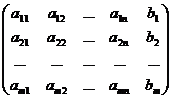 ,
,
которую называют расширенной матрицей системы (1).
Если обозначим
Х =  , С =
, С =  , то систему (1) можно записать в виде матричного уравнения АХ=С.
, то систему (1) можно записать в виде матричного уравнения АХ=С.
