Задача о площади (площадь криволинейной трапеции).

Задача о площади (площадь криволинейной трапеции).

y=f(x) – [a; b], f(x)≥0

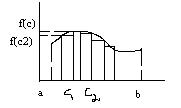
Найти S:

Для решения, разобьем [a; b] на n частичнымх отрезков [xk; xk+1]; a=x0<x1<…<xn=b.

Эти точки xk – разбиение [a;b].

Внутри кажд. частичного отрезка выберем точку Ck принадлеж. [xk; xk+1] и найдем знач. ф-ии в Ck

f(ck),k=0,…n-1

Sn – площаль всех прямоуг-ов: Sn=(x1-x0)f(c1)+(x2-x1)f(c2)+..+f(xn-xn-1)f(Ck)

xk-xk-1=∆xk

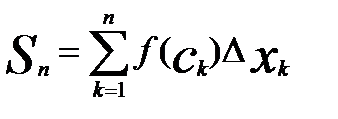(1)

Пусть S – площадь криволин. трапеции, тогда при больших n имеет место приближ рав-во S≈Sn, причем, чем больше отрезков берем, тем точнее рав-во.

Пусть λ=max∆Xk – наиб. из длин частичных отрезков – диаметр разбиения.

Если в (1) перейти к пределу так, чтобы кол-во част. отрез-ов неогран. возрасло и при этом λ->0, то мы получим знач S криволин. трап:

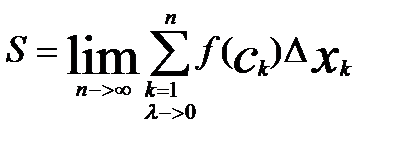
Определённым интеграломфункции f(х) непрерывной на отрезке [а, b] называется предел интегральной суммы, независящий от дробления отрезка [а, b] на частичные и выбора точек a_i когда наибольшая из длин частичных отрезков стремится к нулю.

Интегральная сумма. Свойства интегральных сумм.

Пусть зад ф у=f(x), кот непрер на некот. замкнутом инт-ле [a,b].

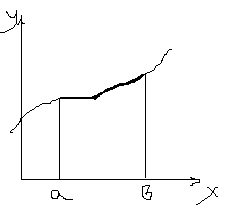
Разбиваем инт-л [a,b] на n частей; абсциссы точек дел-я a=x₀<x₁<x₂<…<x_i-1<x_n-1<x_n=b обозн x₁,x₂,…x_n. Кажд частичный инт-л обозн ∆x₁=x₁-x₀, ∆x₂=x₂-x₁, ∆x_i=x_i-x_i-1, ∆x_n=x_n-x_n-1. В каждом частичном инт-ле ∆x_i , i= 1;n выберем т. и выч-м ﻉ_I , y=f(x), y=f(ﻉ₁) , f(ﻉ₂) , … f(ﻉ_i) ,… f(ﻉ_n) Cост-м произв-е f(ﻉ₁)∆x₁, f(ﻉ₂)∆x₂ , … f(ﻉ_i)∆x_i ,… f(ﻉ_n)∆x_n. Кажд из этих произв-й предст собой полоску шириной ∆x_i и высотой f(ﻉ_i).

Сумма f(ﻉ₁)∆x₁+ f(ﻉ₂)∆x₂ + … f(ﻉ_i)∆x_i +… f(ﻉ_n)∆x_n=∑ f(ﻉ₁)∆x₁ наз интегр суммой ф. f(x) на инт-ле [a,b]. С геом. точки предст собой S ступенчатой фигуры.

Первообразная

Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x ? (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b). Т.: Если F(x) первооб-я ф-и f(x), то F(x)+С тоже пер-я.

Неопределённый интеграл

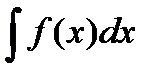Мн-во всех перв-х ф-й F(x)+С для данной ф-и f(x) наз. неопред интегр ф-и f(x) обозн-ся

Стр-ра общего реш-я линейных ДУ 2го порядка

Общее решение ур-я y”+p(x)y’+q(x)y=f(x) есть ф-я вида y(x)=Y(x)+ 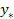(x), в которой Y(x)= 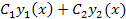– общее решение решение однор.ур-я y”+p(x)y’+q(x)y=0, a 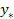(x) – некоторое частное реш-е ур-я y”+p(x)y’+q(x)y=f(x)

Свойства определенного интеграла.

Значение о.и. не зависит от выбора переменной интегрирования:

1.

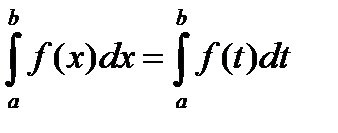
2.

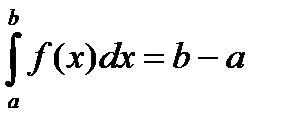
3. 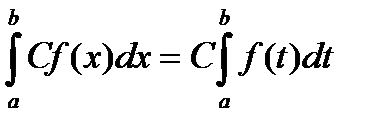С=const

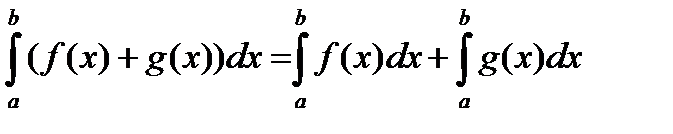
4. 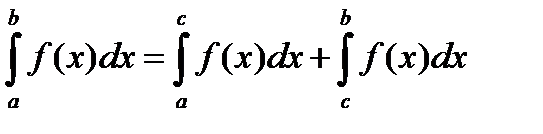для любых a, b, c

5. Если f’(x)>=0, на [a; b] и интегрируема на [a; b ] =>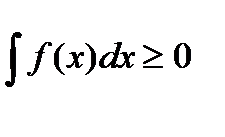

6.f(x)>=g(x), x принадлеж. [a; b], то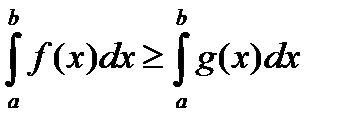

7. пусть f(x) – непрерывна на [a; b ] и m=min f(x), M=max f(x), тогда имеют место неравенства:

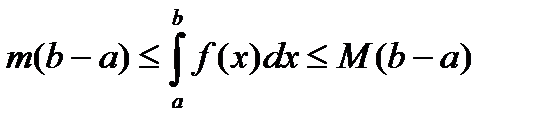
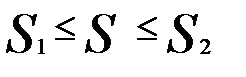
8. Т. О среднем значении если f(x)непрерывна на отрезке [a,b] то сущ.на этом отрезке такая т-ка что ∫_a^bf(x)dx=f(c)(b-a).

Интеграл с переменным верхним пределом и его свойства.

Пусть f(x) непрерывна на отрезке [a,b] тогда она интегрируема на этом отрезке и зн.интегрируема на любом отрезке [a,х] содержащимся в [a,b].

Рассм.ф-цию Ф(х)=∫_а^х f(x)dx- её наз.интегралом с переменным верхним пределом.

Св-ва:

1. Ф(х) непрерывна на [a; b]

2. Если f(x) – непрер. на [a; b], то Ф(х) – дифф-ма на [a; b] и Ф’(x)=f(x).

Таблица основных неопределенных интегралов.

1. ò0dх=С.

2. 2.òхdх= х+С.

3. 3. òх^adх= 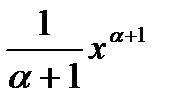+С, a¹1.

4. òсоsхdх=sinх+С; 5. òsinхdх= –соsх+С;

6. ò 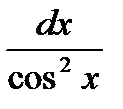=tgх+С; 7. ò 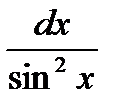=-сtgх+С;

8. ò 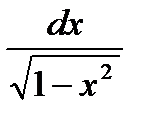= 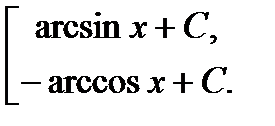; 8а. ò = ;

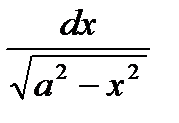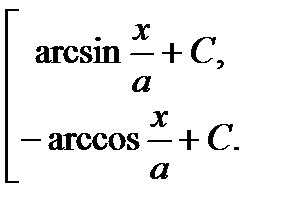9. ò 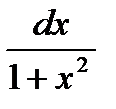= 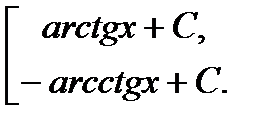; 9а. ò = ;

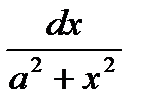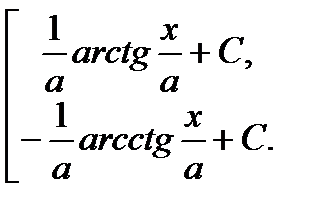10. òа^хdх=а^х/lnх+С; 10а. òе^хdх= е^х + С;

11. ò 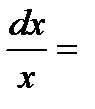ln|х|+С;12.ò 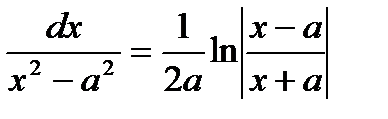+С; 13 ò 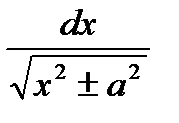=ln|х+ 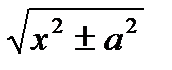|+С

Формула Ньютона-Лейбница.

Если ф-ция f(х) непрерывна на [a,b] и ф-я F(x) какая-либо первообразная для f(x) на отрезке[a,b] то справедлива формула

.

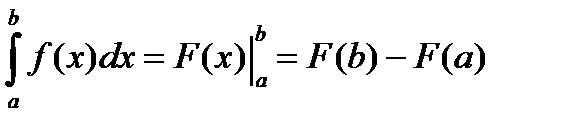Док-во:

пусть F(x)первообразная для f(x) на отрезке [a,b], ф-ция Ф(х) так же явл.первообразной. по теореме о множестве первообразных имеем Ф(х)-F(x)=C. Подставим в последнее рав-во вместо х сначала а, потом b=х получим:

Ф(а)-F(a)=C Ф(b)-F(b)=C Ф(а)=∫_a^a f(x)dx=0 Ф(b)=∫_a^b f(x)dx

Имеем C=-F(a) ∫_a^b f(x)dx+F(a)=F(b) ∫_a^b f(x)dx=F(b)-F(a)

17.Опред. интеграл в эк-ке:

u=f(t) – пр-ть труда, тогда V прод-ии, произвед. за время от t до t2 равен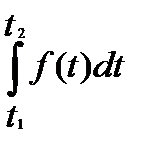

Пусть ф-ия k(x) опред. зависим. TC от Q прод-ии x, тогда f знач. TC при выпуске Q от а до b, x принадлеж. [a; b], опред.: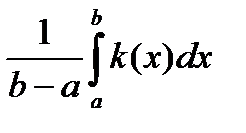

Частные пр-е 1го порядка

Рассм ф-ю 2 перем. z=f(x,y), где x,y 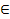Ω с 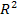.Возьмём любую точку 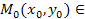Ω, через ∆x и ∆y обозначим приращение по х и у, тогда полное приращение имеет вид:∆z=f( 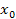+∆x, 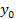+∆y)-f( 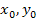). Рассм. отн-е частного прир-я по пер-й z к вызвавшему его прир-ю: рассм. предел, когда ∆x→0, этот предел может существовать и не сущ-ть. Если сущ-т, то он наз. 1й част. пр-й по пер-й х ( 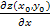, z`x):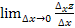

Для того, чтобы находить 1й част. пр-е примен. след правило: 1я част. пр-я по х – это обыкн. пр-я по пер-й х при усл., что у=const

Длина дуги плоской кривой.

Пусть некот. линия y=f(x), где f(x) – дифф. на отрезке [a; b]

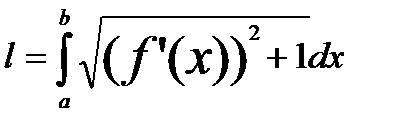- длина дуги АВ

Y(k-1) M(k-1)

M1

Yk A Mk

M(n-1) B

a=x0 x1 x2 xk x(n-1) b=xn

Неберущиеся интегралы.

Опрерация дифференц-я не выводит нас из класса элемент.ф-й. С операцией интегрир. дело обстоит иначе: интегралы от некот. элемент. ф-й уже не явл. элемент. ф-ми. Например: 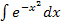– интег. Пуассона; 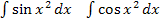– инт. Френеля;

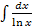– интег.логарифм,

Градиент ф-и

Рассм ф-ю 2 перем. z=f(x,y) 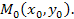Вектор коорд. кот.=1м част. пр-м, вычисленным в т. 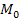и называется градиентом ф-и. Градиент имеет обозначение: grad f(палочка вниз и внизу её 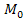)=( )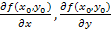. Градиент, вычисленный в т. 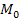хар-ет направ. и велич. макс. скорости возраст. ф-и в указ точке.

Ряды Тейлора и Маклорена.

Пусть f(x) имеет производные всех порядков некотор. окрестн. т. x. Рядом Тейлора для f(x) в т. х0 назыв. степен. ряд след. вида: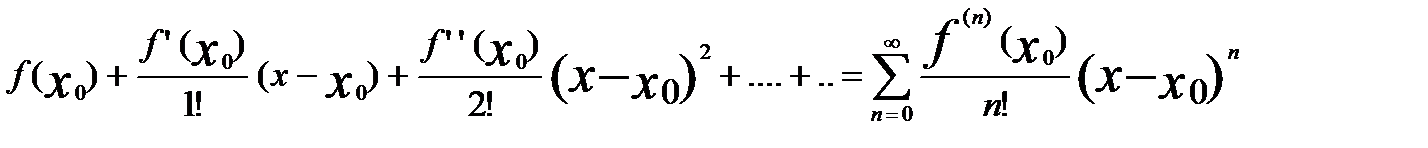

Если х0=0, то ряд

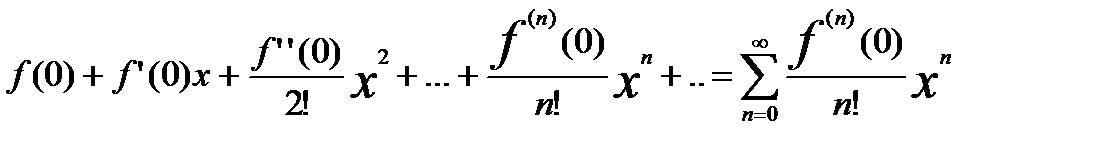
назыв. рядом Маклорена

При выполнении некотр. условий ряд Тейлора для f(x) равен самой f(x). Говорят, что ф-ия представима в виде ф-ии степен. ряда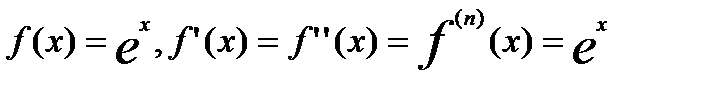

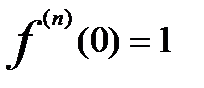
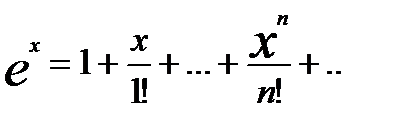x принадлеж. R.

Задача о площади (площадь криволинейной трапеции).

y=f(x) – [a; b], f(x)≥0

Найти S:

Для решения, разобьем [a; b] на n частичнымх отрезков [xk; xk+1]; a=x0<x1<…<xn=b.

Эти точки xk – разбиение [a;b].

Внутри кажд. частичного отрезка выберем точку Ck принадлеж. [xk; xk+1] и найдем знач. ф-ии в Ck

f(ck),k=0,…n-1

Sn – площаль всех прямоуг-ов: Sn=(x1-x0)f(c1)+(x2-x1)f(c2)+..+f(xn-xn-1)f(Ck)

xk-xk-1=∆xk

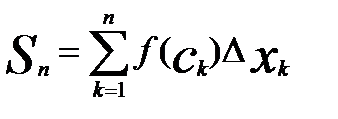(1)

Пусть S – площадь криволин. трапеции, тогда при больших n имеет место приближ рав-во S≈Sn, причем, чем больше отрезков берем, тем точнее рав-во.

Пусть λ=max∆Xk – наиб. из длин частичных отрезков – диаметр разбиения.

Если в (1) перейти к пределу так, чтобы кол-во част. отрез-ов неогран. возрасло и при этом λ->0, то мы получим знач S криволин. трап:

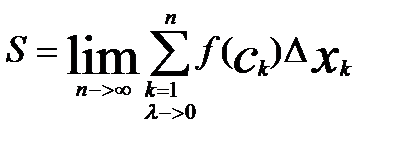
Определённым интеграломфункции f(х) непрерывной на отрезке [а, b] называется предел интегральной суммы, независящий от дробления отрезка [а, b] на частичные и выбора точек a_i когда наибольшая из длин частичных отрезков стремится к нулю.