Тема: Погрешности вычислений
Применение любого численного метода требует оценки погрешности результата вычислений - это непременная составная часть любого серьёзного применения численного метода.
При численном решении задач возникают три типа погрешностей:
погрешности в исходной информации из-за неточных измерений, грубых просчётов или невозможности представить нужную величину конечной дробью;
погрешности ограничения, когда бесконечный математический процесс ограничивается конечным числом операций, определяемых выбором того или иного численного метода при решении задачи;
погрешности округления, связанные с необходимостью представлять числа в виде конечной последовательности цифр, заносимых в ограниченную разрядную сетку ЭВМ.
Введём обозначения: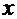 
- точное значение; 
- приближённое значение; тогда абсолютная погрешность 
;
относительная погрешность 
.
В знаменателе относительной погрешности стоит приближённое значение, так как точное значение неизвестно.
Обычно 
измеряется в % и чем меньше , тем выше точность вычислений. Абсолютную погрешность 
записывают с 1-2 значащими цифрами, и округление погрешности выполняют в сторону её увеличения.
Значащими цифрами называют все цифры числа, кроме нулей левее первой отличной от нуля цифры и тех нулей в конце числа, которые заменяют отброшенные или неизвестные цифры.
Задача 1. Заданы веса 4-х грузов и абсолютные погрешности взвешиваний. Определить относительные погрешности во всех вариантах взвешиваний и найти среди них наиболее точное взвешивание.
| Вес |  |  | |  | | |
| 0,5кГ 1,3кГ 5,31кГ 50кГ | 1Г | 0,2*10-2 0,77*10-3 0,19*10-3 0,2*10-4 | 10Г | 0,2*10-1 0,77*10-2 0,19*10-2 0,2*10-3 | 5мГ | 0,1*10-4 0,39*10-5 0,95*10-6 0,1*10-6 |
Задача 2. Измерены 4 расстояния и заданы относительные погрешности измерений. Определить абсолютные погрешности измерений.
| Рассто- яния | | | | | | |
| 500м 3,5км 10м 1,25м | 0,1 | 50м 0,35км 1м 0,13м | 0,1% | 0,5м 0,0035км 0,01м 0,0013м | 5% | 25м 0,18км 0,5м 0,063м |
Задача 3. Для приближённых равенств найти наибольший промежуток [0;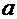 
], на котором абсолютная погрешность не превышает заданного значения 
.
1) 
заданная абсолютная погрешность 
.
Решение. 
При наибольшее значение 
.
2) 
заданная абсолютная погрешность 
. Решение. 
, откуда
пренебрегаем 
под 
и выбираем больший корень уравнения 
.
При наибольшее значение 
.
Верные знаки числа
В приближённом числе цифра называется верной, если абсолютная погрешность числа не превосходит единицы его разряда. Все предшествующие цифры этого числа тоже верные, а за последней верной цифрой следуют сомнительные.
Под числом верных десятичных знаков числа понимают число верных цифр после запятой.
Пример. Пусть все цифры чисел верные.
| Числа | Кол-во верных знаков | Кол-во верных десят. Знаков |
| 0,002405 27,034 |
Обычно в промежуточных вычислениях сохраняют кроме верных цифр 1-2 сомнительных, а в окончательном результате не более одной сомнительной цифры.