Метод Пикара – приближённый аналитический метод.

Задача Коши: решить ОДУ y` = f(x,y) c начальным условием y(x₀)=y_0/

Задача Коши имеет единственное решение, если функция f(x,y) непрерывна в окрестности точки (x₀,y₀) и имеет ограниченную частную производную по y – f`_y.

Формула Пикара: .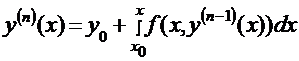

В области R{|x-x₀|<a;|y-y₀|<b} погрешность оценивается формулой:

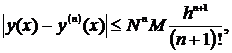
где M=max|f(x,y)|; N=max|f`_y(x,y)|; h=min(a,b/M).

Пример. Методом Пикара найти три первых приближённых решения дифференциального уравнения и оценить погрешность:

y`=x-y; y(x=0)=1; на отрезке [0;0,5]. ;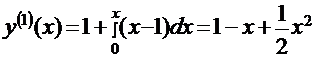

;

;

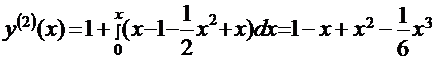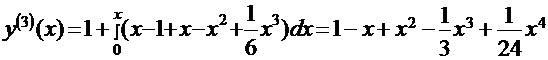X	X2	X3	X4	Y(1)	Y(2)	Y(3)
				1,	1,	1,
0,1	0,01	0,001	0,0001	0,9050	0,9098	0,9098
0,2	0,04	0,008	0,0016	0,8200	0,8397	0,8377
0,3	0,09	0,027	0,0081	0,7450	0,7855	0,7650
0,4	0,16	0,064	0,0256	0,6800	0,7494	0,7397
0,5	0,25	0,125	0,0625	0,6250	0,7292	0,7109

Для оценки погрешности каждого из приближённых решений вычислим.

n=1: x=[0;0,5]; y=[1;0,625]; f(x,y)=x-y; max|f(x,y)| =1=M;

f`<sub>y</sub>(x,y)=x-1; max|f`(x,y)|=1=N;

h=min(|x-x₀|=0,5;|y-y₀|=0,375)=0,375;

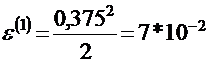- погрешность первого приближения.

n=2: x=[0;0,5]; y=[1;0,7292]; M=1; N=1; h=min(0,5;0,2708)=0,2708;

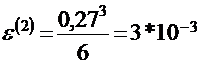-погрешность второго приближения.

n=3: x=[0;0,5]; y=[1;0,7109]; M=1; N=1; h=min(0,5;0,29)=0,29;

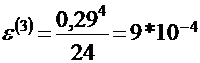-погрешность третьего приближения.

Метод Эйлера – численный метод первого порядка точности.

Расчётная формула: 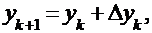где .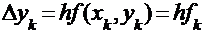

Оценку погрешности выполняют методом Рунге путём двойного просчёта: с шагом h – y_n, и с шагом h/2 – y^*_n.. Пусть y(x_n) – точное решение в точке x_n, тогда погрешность в этой точке:

|y^*_n – y(x_n)| < |y^*_n – y_n| .

Пример. Решить дифференциальное уравнение 1-го порядка : y`=y – 2x/y c начальным условием y(x=0)=1 на интервале [0;1] c шагом h=0,2.

k	xk	yk	F(xk,yk)	yk	yточное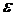
		1,0000	1,0000	0,2000	1,0000
	0,2	1,2000	0,8667	0,1733	1,1832	0,0168
	0,4	1,3733	0,7805	0,1581	1,3416	0,0317
	0,6	1,5315	0,7458	0,1495	1,4832	0,0483
	0,8	1,6811	0,7254	0,1458	1,6124	0,0687
	1,0	1,8268			1,7320	0,0948

Метод Эйлера даёт грубое приближение к точному решению и по мере удаления от начальной точки погрешность растёт.

Усовершенствованный метод Эйлера 2-го порядка ( )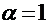

Расчётная формула: 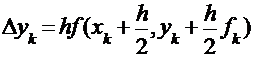; 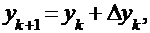Здесь выполняется корректировка наклона интегральной кривой в средней точке каждого шага.

Погрешность оценивается методом Рунге путём двойного просчёта по формуле: |y^*_n – y(x_n)| < 1/3|y^*_n - y_n| . Причём погрешность следует вычислять для каждой точки приближённого решения c шагом h.

Пример. Решить дифференциальное уравнение из предыдущего примера усовершенствованным методом Эйлера.

k	xk	yk	(h/2)fk	xk+h/2	yk+(h/2)fk	yk	yточное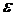
		1,0000	0,1	0,1	1,1000	0,1836	1,0000
	0,2	1,1836	0,0846	0,3	1,2682	0,1590	1,1832	0.0004
	0,4	1,3426	0,0747	0,5	1,4173	0,1424	1,3416	0,0010
	0,6	1,4850	0,0677	0,7	1,5527	0,1302	1,4832	0,0018
	0,8	1,6152	0,0625	0,9	1,6777	0,1210	1,6124	0,0028
	1,0	1,7362					1,7320	0,0042

Трудоёмкость вычислений возросла – правая часть дифференциального уравнения вычисляется дважды.

Метод Эйлера-Коши 2-го порядка точности ( )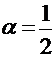

Расчётная формула: ;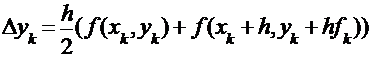

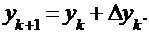
Погрешность оценивается по той же формуле, что и в усовершенствованном методе Эйлера, и правая часть дифференциального уравнения вычисляется дважды.

Пример. Решить дифференциальное уравнение из предыдущего примера

методом Эйлера-Коши.

k	xk	yk	f(xk,yk)	xk+h	yk+hfk	f(xk+h,yk+hfk)	yk	yточное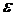
		1,0	1,0000	0,2	1,2000	0,8667	0,1867	1,0000
	0,2	1,1867	0,8497	0,4	1,3566	0,7669	0,1617	1,1832	0,0035
	0,4	1,3484	0,7551	0,6	1,4994	0,6991	0,1454	1,3416	0,0068
	0,6	1,4938	0,6905	0,8	1,6319	0,6515	0,1342	1,4832	0,0106
	0,8	1,6280	0,6452	1,0	1,7570	0,6187	0,1264	1,6124	0,0156
	1,0	1,7544						1,7320	0,0224

Метод Рунге-Кутта 4-го порядка точности

На каждом i-ом шаге вычисляют 4 числа:

K₁ = hf(x_i,y_i); K₂ = hf(x_i+h/2,y_i+k₁/2); K₃ = hf(x_i+h/2,y_i+k₂/2); K₄ = hf(x_i+h,y_i+k₃)

и определяют их средневзвешенное по формуле:

y_i = 1/6(K₁+2K₂+2K₃+K₄); y_i+1 = y_i+ y_i .

Погрешность оценивается методом Рунге по формуле:

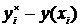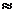| | 1/15| |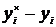

При ручных расчётах целесообразно формировать следующую таблицу .

i	x	y	y`=f(x,y)	K=h f	y
	x0	y0	f(x0,y0)	K1(0)	K1(0)
	x0+h/2	y0+k1/2	f(x0+h/2, y0+k1/2)	K2(0)	2 K2(0)
	x0+h/2	y0+k2/2	f(x0+h/2, y0+k2/2)	K3(0)	2 K3(0)
	x0+h	y0+k3	f(x0+h, y0+k3)	K4(0)	K4(0)
					1/6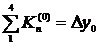
	x1	y1=y0+ y0	f(x1,y1)	K1(1)	K1(1)
	x1+h/2	y1+k1/2	f(x1+h/2,y1+k1/2)	K2(1)	2K2(1)
	x1+h/2	y1+k2/2	f(x1+h/2,y1+k2/2)	K3(1)	2K3(1)
	x1+h	y1+k3	f(x1+h, y1+k3)	K4(1)	K4(1)
					1/6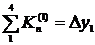
	x2	y2=y1+ y1

Пример. Найти решение дифференциального уравнения y` = y/x – y²

c начальным условием y(x=1) = 1 на отрезке [1;2] с шагом h=0,2 методом Рунге – Кутта 4-го порядка точности.

i	x	y	f(x,y)	k=hf	y
	1,0
	1,1	1,0000	-0,0909	-0,0182	-0,0364
	1,1	0,9909	-0,0811	-0,0162	-0,0324
	1,2	0,9838	-0,1480	-0,0296	-0,0296
					-0,0164
	1,2	0,9016	-0,0616	-0,0123	-0,0123
	1,3	0,8954	-0,1130	-0,0226	-0,0452
	1,3	0,8903	-0,1078	-0,0216	-0,0431
	1,4	0,8800	-0,1459	-0,0292	-0,0292
					-0,0216
	1,4	0,7718	-0,0444	-0,0089	-0,0089
	1,5	0,7674	-0,0773	-0,0156	-0,0310
	1,5	0,7641	-0,0744	-0,0149	-0,0298
	1,6	0,7569	-0,0998	-0,0200	-0,0200
					-0,0149
	1,6	0,6823	-0,0391	-0,0078	-0,0078
	1,7	0,6794	-0,0611	-0,0122	-0,0245
	1,7	0,6762	-0,0595	-0,0119	-0,0238
	1,8	0,6704	-0,0770	-0,0154	-0,0154
					-0,0119
	1,8	0,6108	-0,0338	-0,0068	-0,0068
	1,9	0,6074	-0,0493	-0,0099	-0,0197
	1,9	0,6059	-0,0482	-0,0096	-0,0193
	2,0	0,6012	-0,0608	-0,0122	-0,0122
					-0,0097
	2,0	0,5529