ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 6. 7. 8

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 6. 7. 8

Тема: Приближённые методы решения обыкновенных дифференциальных уравнений.

Метод Пикара – приближённый аналитический метод.

Задача Коши: решить ОДУ y` = f(x,y) c начальным условием y(x₀)=y_0/

Задача Коши имеет единственное решение, если функция f(x,y) непрерывна в окрестности точки (x₀,y₀) и имеет ограниченную частную производную по y – f`_y.

Формула Пикара: .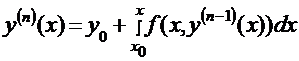

В области R{|x-x₀|<a;|y-y₀|<b} погрешность оценивается формулой:

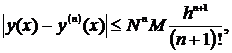
где M=max|f(x,y)|; N=max|f`_y(x,y)|; h=min(a,b/M).

Пример. Методом Пикара найти три первых приближённых решения дифференциального уравнения и оценить погрешность:

y`=x-y; y(x=0)=1; на отрезке [0;0,5]. ;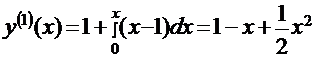

;

;

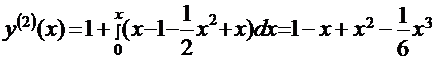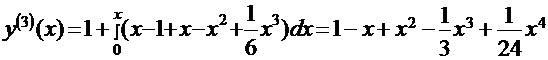X	X2	X3	X4	Y(1)	Y(2)	Y(3)
				1,	1,	1,
0,1	0,01	0,001	0,0001	0,9050	0,9098	0,9098
0,2	0,04	0,008	0,0016	0,8200	0,8397	0,8377
0,3	0,09	0,027	0,0081	0,7450	0,7855	0,7650
0,4	0,16	0,064	0,0256	0,6800	0,7494	0,7397
0,5	0,25	0,125	0,0625	0,6250	0,7292	0,7109

Для оценки погрешности каждого из приближённых решений вычислим.

n=1: x=[0;0,5]; y=[1;0,625]; f(x,y)=x-y; max|f(x,y)| =1=M;

f`<sub>y</sub>(x,y)=x-1; max|f`(x,y)|=1=N;

h=min(|x-x₀|=0,5;|y-y₀|=0,375)=0,375;

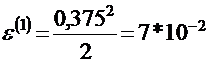- погрешность первого приближения.

n=2: x=[0;0,5]; y=[1;0,7292]; M=1; N=1; h=min(0,5;0,2708)=0,2708;

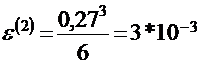-погрешность второго приближения.

n=3: x=[0;0,5]; y=[1;0,7109]; M=1; N=1; h=min(0,5;0,29)=0,29;

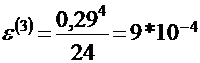-погрешность третьего приближения.

Метод Эйлера – численный метод первого порядка точности.

Расчётная формула: 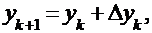где .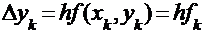

Оценку погрешности выполняют методом Рунге путём двойного просчёта: с шагом h – y_n, и с шагом h/2 – y^*_n.. Пусть y(x_n) – точное решение в точке x_n, тогда погрешность в этой точке:

|y^*_n – y(x_n)| < |y^*_n – y_n| .

Пример. Решить дифференциальное уравнение 1-го порядка : y`=y – 2x/y c начальным условием y(x=0)=1 на интервале [0;1] c шагом h=0,2.

k	xk	yk	F(xk,yk)	yk	yточное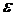
		1,0000	1,0000	0,2000	1,0000
	0,2	1,2000	0,8667	0,1733	1,1832	0,0168
	0,4	1,3733	0,7805	0,1581	1,3416	0,0317
	0,6	1,5315	0,7458	0,1495	1,4832	0,0483
	0,8	1,6811	0,7254	0,1458	1,6124	0,0687
	1,0	1,8268			1,7320	0,0948

Метод Эйлера даёт грубое приближение к точному решению и по мере удаления от начальной точки погрешность растёт.

Усовершенствованный метод Эйлера 2-го порядка ( )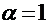

Расчётная формула: 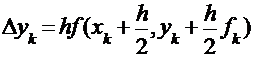; 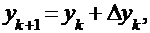Здесь выполняется корректировка наклона интегральной кривой в средней точке каждого шага.

Погрешность оценивается методом Рунге путём двойного просчёта по формуле: |y^*_n – y(x_n)| < 1/3|y^*_n - y_n| . Причём погрешность следует вычислять для каждой точки приближённого решения c шагом h.

Пример. Решить дифференциальное уравнение из предыдущего примера усовершенствованным методом Эйлера.

k	xk	yk	(h/2)fk	xk+h/2	yk+(h/2)fk	yk	yточное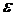
		1,0000	0,1	0,1	1,1000	0,1836	1,0000
	0,2	1,1836	0,0846	0,3	1,2682	0,1590	1,1832	0.0004
	0,4	1,3426	0,0747	0,5	1,4173	0,1424	1,3416	0,0010
	0,6	1,4850	0,0677	0,7	1,5527	0,1302	1,4832	0,0018
	0,8	1,6152	0,0625	0,9	1,6777	0,1210	1,6124	0,0028
	1,0	1,7362					1,7320	0,0042

Трудоёмкость вычислений возросла – правая часть дифференциального уравнения вычисляется дважды.

Метод Эйлера-Коши 2-го порядка точности ( )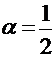

Расчётная формула: ;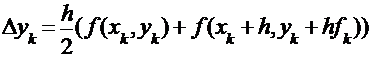

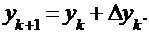
Погрешность оценивается по той же формуле, что и в усовершенствованном методе Эйлера, и правая часть дифференциального уравнения вычисляется дважды.

Пример. Решить дифференциальное уравнение из предыдущего примера

методом Эйлера-Коши.

k	xk	yk	f(xk,yk)	xk+h	yk+hfk	f(xk+h,yk+hfk)	yk	yточное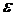
		1,0	1,0000	0,2	1,2000	0,8667	0,1867	1,0000
	0,2	1,1867	0,8497	0,4	1,3566	0,7669	0,1617	1,1832	0,0035
	0,4	1,3484	0,7551	0,6	1,4994	0,6991	0,1454	1,3416	0,0068
	0,6	1,4938	0,6905	0,8	1,6319	0,6515	0,1342	1,4832	0,0106
	0,8	1,6280	0,6452	1,0	1,7570	0,6187	0,1264	1,6124	0,0156
	1,0	1,7544						1,7320	0,0224

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 5, 4

Тема: Методы приближения функций

Пример 2.

Функция задана таблицей с равноотстоящими значениями аргумента. Найти значения y для x=1,217 и x=1,253.

xk	yk	yk	2yk
1,215 1,220 1,225 1,230 1,235 1,240 1,245 1,250 1,255 1,260	0,106044 0,106491 0,106935 0,107377 0,107818 0,108257 0,108696 0,109134 0,109571 0,110008	0,000447 0,000444 0,000442 0,000441 0,000439 0,000439 0,000438 0,000437 0,000437	-0,000003 -0,000002 -0,000001 -0,000002 0,000000 -0,000001 -0,000001 0,000000

В данном примере конечные разности первого порядка практически постоянны, а это приводит к тому, что конечные разности второго порядка близки к нулю.

Чтобы найти значение функции для аргумента x=1,217, находящегося вблизи начала таблицы, воспользуемся 1-ой формулой Ньютона и вычислим:

q =( 1,217 – 1,215 ) : 0,005 = 0,4

Подставляем в 1-ую формулу значения из первой строки таблицы:

y( x=1,217) = 0,106044 + 0,4 (0,000447) + (0,4 (-0,6): 2)(-0,000003)=

= 0,106044 + 0,000179 + 0,0000003 = 0,106223

Чтобы найти значение функции для аргумента x=1,253, находящегося вблизи конца таблицы, воспользуемся 2-ой формулой Ньютона и вычислим:

q =( 1,253 – 1,260 ) : 0,005 = -1,4

Подставляем во 2-ую формулу значения конечных разностей с диагонали таблицы:

y( x=1,253) = 0,110008 + (-1,4) 0,000437 = 0,110008 - 0,000612 = 0,109396

Решение.

k	Xk	Yk	XkYk	Xk2	Ykтеор	Yk-Ykтеор	(Yk-Ykтеор)2
		66,7			67,50	0,20	0,0400
		71,0	284,0		70,98	0,02	0,0004
		76,3	763,0		76,20	0,10	0,0100
		80,6	1209,0		80,55	0,05	0,0025
		85,7	1799,7		85,77	- 0,07	0,0049
		92,9	2694,1		92,73	0,17	0,0289
		99,4	3578,4		98,82	0,58	0,3364
		113,6	5793,6		111,87	1,73	2,9929
		125,1	8506,8		126,66	- 1,56	2,4336
суммы		811,3	24628,6				5,8496

Общее уравнение прямой: .

Система линейных уравнений, из которой следует определять наилучшие значения коэффициентов 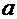и 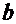, руководствуясь методом наименьших квадратов, имеет вид:

Подставим в систему уравнений вычисленные суммы из 2-го, 3-го, 4-го и 5-го столбцов последней строки таблицы:

Откуда определены коэффициенты линейной зависимости Значит уравнение теоретической прямой имеет вид:

. (*)

В шестом столбце таблицы приведены вычисленные по теоретическому уравнению значений функции для заданных значений аргумента. В седьмом столбце таблицы приведены значения разностей между заданными значениями функции ( 3-ий столбец ) и теоретическими значениями ( 6-ой столбец ), вычисленными по уравнению (*).

В восьмом столбце приведены квадраты отклонений теоретических значений от экспериментальных и определена сумма квадратов отклонений. Теперь можно найти среднее квадратичное отклонение:

Пример 3. Пусть данные эксперимента, приведённые в таблице, аппроксимируются квадратичной параболой: Найти наилучшие значения коэффициентов параболы, применив метод наименьших квадратов.

Решение.

k	Xk	Yk	Xk2	Xk3	Xk4	XkYk	Xk2Yk	Ykтеор	Yk-Ykтеор
		29,8						29,28	0,52	0,2704
		22,9				45,8	91,6	22,22	0,68	0,4624
		17,1				68,4	273,6	17,60	-0,50	0,2500
		15,1				75,5	377,5	15,56	-0,46	0,2116
		10,7				85,6	684,8	11,53	-0,83	0,6889
		10,1				101,0	1010,0	10,60	-0,50	0,2500
		10,6				127,2	1526,4	11,06	-0,46	0,2116
		15,2				228,0	3420,0	14,38	0,82	0,6724
Сум		122,5				731,5	7383,9			3,0173

Система линейных уравнений для определения коэффициентов параболы имеет вид:

Из последней строки таблицы в систему уравнений подставляют соответствующие суммы:

Решение системы уравнений позволяет определить значения коэффициентов:

Итак, заданная таблицей зависимость на отрезке [0;15] аппроксимируется квадратичной параболой:

Расчёт по приведённой формуле для заданных значений аргумента позволяет сформировать девятый столбец таблицы, содержащий теоретические значения функции.

Сумма квадратов отклонений теоретических значений от экспериментальных приведена в последней строке 11-го столбца таблицы. Это позволяет определить среднее квадратичное отклонение:

.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3

Тема: Методы решения систем уравнений

Метод Гаусса - метод последовательного исключения неизвестных – относится к группе точных методов, и если бы отсутствовала погрешность вычислений, можно было бы получить точное решение.

При ручных расчётах вычисления целесообразно вести в таблице, содержащей столбец контроля. Ниже представлен общий вариант такой таблицы для решения системы линейных уравнений 4-го порядка.

				Свободные члены	Столбец контроля

				Свободные члены	Столбец контроля

Пример 1. Методом Гаусса решить систему уравнений 4-го порядка:

Вычисления следует вести в таблице со столбцом контроля, образец которой приведён выше.

				Свободные члены	Столбец контроля
2	-1	-1		-1
		0,5		4,5
	2 -1	-1,5 1,5	-1 -3 -1	3,5 -4 -5,5	-6 -6
		-0,75	-0,5	1,75	1,5
		0,75 0,75	-2,5 -1,5	-5,75 -3,75	-7,5 -4,5
			-3,33	-7,67	-10

Пример 2. Найти корни линейной системы уравнений 3-го порядка:

Составляется аналогичная таблица для определения значений трёх

неизвестных корней системы уравнений.

			Свободные члены	Столбец контроля
-1 -1	-1 -1	-1 -1	11,33	15,33
	-,167	-0,167	1,89	2,56
	5,83 -1,17	-1,17 5,83	33,9 43,9	38,6 48,6
		-0,20	5,80	6,60
		5,60	50,7	56,3
			9,05	10,05

Эти приближённые значения корней можно подставить в исходную систему уравнений и вычислить невязки - , являющиеся разностями между правой и левой частями каждого уравнения системы при подстановке в левую часть найденных корней. Затем подставляются в качестве свободных членов системы невязки и получают поправки

корней - :

Метод простой итерации

После приведения системы уравнений к каноническому виду выбирают «нулевое» приближение – обычно столбец свободных членов, и каждое новое приближение вычисляют по предыдущему, руководствуясь формулой: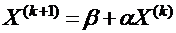

Вычисления следует закончить, когда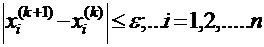

Пример 3. Методом простой итерации решить систему уравнений:

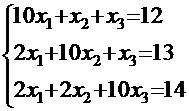
Условия сходимости (2) выполняются, значит, итерационный процесс будет сходиться. Приведём систему к каноническому виду, выразив из первого уравнения, из второго, из третьего уравнения.

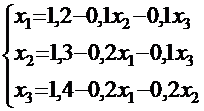
За «нулевое» приближение примем столбец свободных членов:

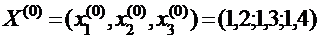
Подставляем в систему уравнений вектор «нулевого» приближения – получаем первое приближение:

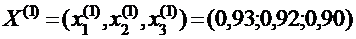
Продолжая этот процесс, получаем последовательность приближений:

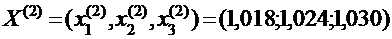
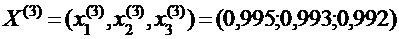
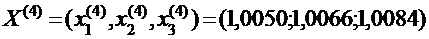
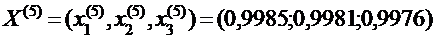
Корни получены с точностью до 10^-2: 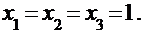Из приведённой последовательности приближений видно, что приближённые значения корней колеблются вокруг точных значений.

Процесс уточнения корней можно продолжить, если задана более высокая степень точности.

Итерационный метод Зейделя

Для ускорения процесса уточнения корней предложено усложнить вычислительную процедуру, включая в вычисления на каждой итерации приближённые значения корней, полученные на текущей итерации. Этот приём позволяет нередко решать системы, которые не решаются методом

простой итерации.

Условия сходимости метода Зейделя те же, что и для метода простой итерации. Их необходимо проверять перед началом расчёта.

Схема расчёта представлена в следующей системе уравнений:

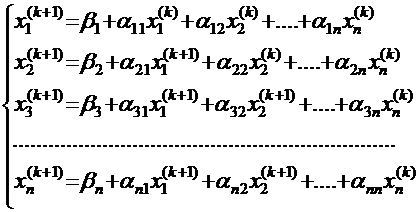
Расчёт следует продолжать до тех пор, пока не совпадут с заданной степенью точности два последовательных приближения каждого из корней системы уравнений.

Погрешность оценивается через нормы матрицы коэффициентов по формуле:

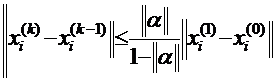
Пример 4. Методом Зейделя найти корни линейной системы уравнений с точностью до 10^-3:

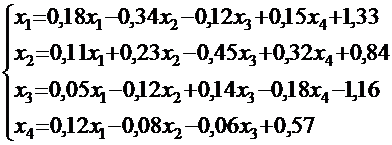
В качестве «нулевого» приближения взят столбец свободных членов, а результаты расчёта по схеме Зейделя приведены в таблице.

Номер итерации	X1	X2	X3	X4
	-1,6303	1,5583	-1,6935	0,3974
	-1,8904	1,8797	-1,7887	0,3862
	-2,0368	1,9768	-1,8190	0,3746
	-2,0943	2,0027	-1,8271	0,3693
	-2,1132	2,0085	-1,8289	0,3674
	-2,1187	2,0095	-1,8293	0,3668
	-2,1201	2,0095	-1,8292	0,3666
	-2,1203	2,0094	-1,8292	0,3666
	-2,1204	2,0094	-1,8292	0,3666
	-2,1204	2,0094	-1,8292	0,3666

Уточнения корней продолжались до тех пор, пока у корня X₁ не совпали значащие цифры в 9-ой и 10-ой итерациях, а корни X₂, X₃ и X₄ определены с заданной точностью на предыдущих итерациях.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

Метод касательных Ньютона

Расчётная формула: .

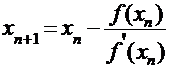Этот метод также требует сужения интервала изоляции до выполнения неравенства: 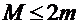. За нулевое приближение следует брать неподвижный конец интервала изоляции корня, иначе процесс приближения к корню будет расходящимся.

Расчётная таблица имеет следующий вид.

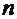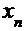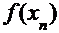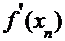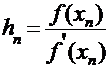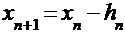Приме 2.. Найти корень нелинейного уравнения с точностью до 10^-5 методом касательных: 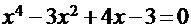на интервале [-3;-2].

Решение.

На концах интервала изоляции функция имеет разные знаки: 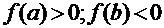; знак второй производной 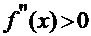. Значит, неподвижным является левый конец интервала – точка 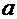, который в методе касательных и станет нулевым приближением к корню .

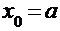Для выполнения неравенства 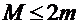необходимо сузить интервал изоляции до [-2,31;-2,29], тогда 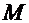=58,0332, 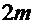=60,5919.

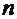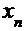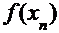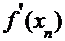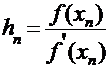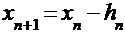	-2,310000 -2,302824 -2,302776	0,225663 0,001491 0,000000	-31,445564 -31,030526 -31,027757	-0,007176 -0,000048 -0,000000	-2,302824 -2,302776 -2,302776

Метод итераций

Этот метод требует приведения исходного уравнения к каноническому виду: 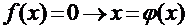. Тогда одношаговый итерационный процесс строится по формуле: 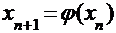при выборе любого нулевого приближения из интервала изоляции.

Главное - проверка соблюдения условий сходимости для канонического уравнения: 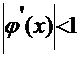- это обеспечит сходящийся итерационный процесс и получение значения корня уравнения с требуемой точностью за конечное число шагов.

Существует стандартный приём преобразования уравнения к каноническому виду, обеспечивающий сходимость итерационного процесса. 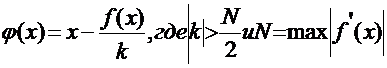. Знак 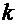совпадает со знаком первой производной исходной функции. Итерации продолжают до тех пор, пока не будет выполнено условие:

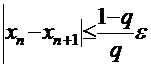, где 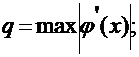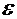- погрешность.

Если функция 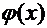возрастает, приближённые значения сходятся к точному значению корня монотонно, если же функция 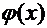убывает, то приближённые значения колеблются вокруг точного значения.

Пример 3.

Для функции 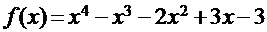найти интервалы изоляции действительных корней и на каждом интервале привести исходное уравнение к каноническому виду, используя стандартный приём, и проверить выполнение условий сходимости итерационного процесса.

Решение.

Построение графика функции выявило два действительных корня уравнения на интервалах [-2;-1] и [1;2].

Для применения стандартного приёма преобразования уравнения к каноническому виду необходимо найти максимум первой производной:

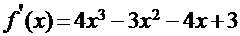
Интервал [-2;-1] : .

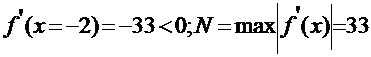Следовательно, положим 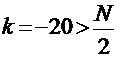и знак совпадает со знаком .

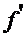Тогда правая часть канонического уравнения:

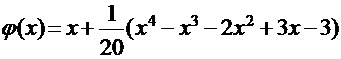
Проверим выполнение условия сходимости:

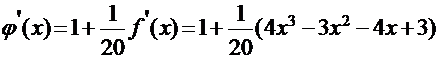
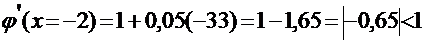
Интервал [1;2] : .

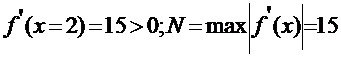Следовательно, положим 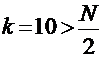и знак совпадает со знаком .

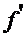Тогда правая часть канонического уравнения:

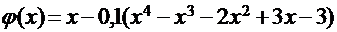
Проверим выполнение условия сходимости:

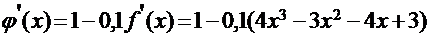
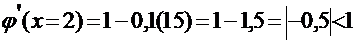
Таким образом, на каждом из интервалов условия сходимости выполняются для канонических уравнений, которые получены с помощью стандартной схемы преобразования исходного уравнения.

Пример 4. Найти корень нелинейного уравнения 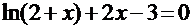на интервале [0,1;1] с точностью до 10^-5.

Решение. Для приведения исходного уравнения к каноническому виду можно использовать стандартный приём, а можно попробовать выразить 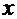из уравнения и проверить выполнение условия сходимости.

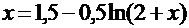
Сходимость итерационного процесса обеспечена, если 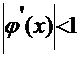. Найдём первую производную от правой части канонического уравнения.

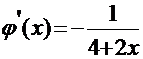
Вычислим значения производной на концах интервала 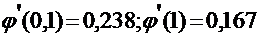- условия сходимости выполняются, следовательно, итерационный процесс будет сходящимся.

Выберем начальное приближение 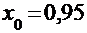и последующие вычисления представлены в таблице. Расчётная формула: .

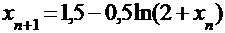n		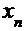	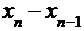комментарий
	0,95000000
	0,95909741	0,00909741	>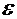
	0,95755785	0,00153956	>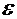
	0,95781806	0,00026021	>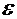
	0,95777407	0,00004399	>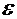
	0,95778151	0,00000744	<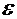

Значение корня с точностью 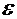=0,00001: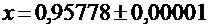

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

Верные знаки числа

В приближённом числе цифра называется верной, если абсолютная погрешность числа не превосходит единицы его разряда. Все предшествующие цифры этого числа тоже верные, а за последней верной цифрой следуют сомнительные.

Под числом верных десятичных знаков числа понимают число верных цифр после запятой.

Пример. Пусть все цифры чисел верные.

Числа	Кол-во верных знаков	Кол-во верных десят. Знаков
0,002405 27,034

Обычно в промежуточных вычислениях сохраняют кроме верных цифр 1-2 сомнительных, а в окончательном результате не более одной сомнительной цифры.

Разработка

практических занятий по дисциплине

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

с примерами решения задач по темам

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 6. 7. 8

Тема: Приближённые методы решения обыкновенных дифференциальных уравнений.