Приближенное решение алгебраических уравнений.

Точные методы решения уравнений подходят только к узкому классу уравнений (квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические).
В общем случае решение данного уравнения находится приближённо в следующей последовательности:
1) отделение (локализация) корня;
2). Отделение корня. Отделение действительного корня уравнения - это нахождение отрезка , в котором лежит только один корень данного уравнения. Такой отрезок называется отрезком изоляции (локализации) корня.
Наиболее удобным и наглядным является графический метод отделения корней:
1) строится график функции , и определяются абсциссы точек пересечения этого графика с осью , которые и являются корнями уравнения ;
2) если - сложная функция, то её надо представить в виде так, чтобы легко строились графики функций и . Так как , то . Тогда абсциссы точек пересечения этих графиков и будут корнями уравнения .

Интерполяция

Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называетсяаппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса-Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.

Определения

Рассмотрим систему несовпадающих точек 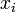( 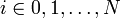) из некоторой области 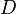. Пусть значения функции 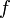известны только в этих точках:

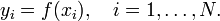
Задача интерполяции состоит в поиске такой функции 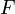из заданного класса функций, что

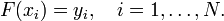
§ Точки 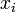называют узлами интерполяции, а их совокупность — интерполяционной сеткой.

§ Пары 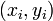называют точками данных или базовыми точками.

§ Разность между «соседними» значениями — шагом интерполяционной сетки. Он может быть как переменным так и постоянным.

§ Функцию 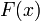— интерполирующей функцией или интерполянтом.

Пример

1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений 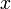определяет соответствующие значения :

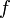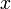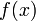	0,8415
	0,9093
	0,1411
	−0,7568
	−0,9589
	−0,2794

Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).

К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.

2. Найти промежуточное значение (способом линейной интерполяции).

	15.5
	?
	19.2

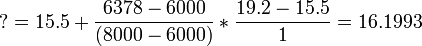
Преподаватель: Меркачева Л.И.

ЛИТЕРАТУРА:

1. И.С. Пискунов «Дифференцированное и интегральное исчисление».
2. Р.С. Гутер., П.Т. Резниковский «Программирование и вычислительная математика».
3. В.П. Григорьев, Ю.А. Дубинский «Элементы высшей математики».
4. Н.В. Богомолов «практическое занятие по математике».