Площадь криволинейной трапеции
Площадь криволинейной трапеции
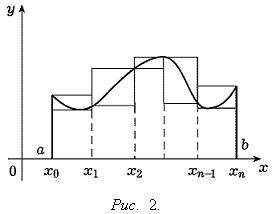
Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте [a, b] непрерывной и неотрицательной фукнции f(x), ординатами, проведенными в точках a и b, и отрезком осиOx между точками a и b (см. Рис. 2).
Докажем следующее утверждение.
Криволинейная трапеция представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле
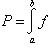
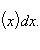 (1)
(1)
Доказательство. Так как непрерывная на сегменте [a, b] функция интегрируема, то для любого положительного числа ε можно указать такое разбиение T сегмента [a, b], что разность S - s < ε, где S и s - соответственно верхняя и нижняя суммы разбиения T. Но S и s равны соответственно Sd и Si, где Sd и Si - площади ступенчатых фигур (многоугольников), первая из которых содержит криволинейную трапецию, а вторая содержится в криволинейной трапеции (на Рис. 2 изображены также и указанные ступенчатые фигуры). Так как Sd - Si < ε, то, в силу теоремы 1, криволинейная трапеция квадрируема. Поскольку предел при Δ → 0 верхних и нижних сумм равен 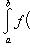
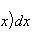 и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле (1).
и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле (1).
Замечание. Если функция f(x) непрерывна и неположительна на сегменте [a, b], то значение интеграла 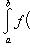
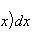 равно взятой с отрицательным знаком площади криволинейной трапеции, ограниченной графиком функции f(x), ординатами в точках a и b и отрезком оси Ox между точками a и b. Поэтому, еслиf(x) меняет знак, то
равно взятой с отрицательным знаком площади криволинейной трапеции, ограниченной графиком функции f(x), ординатами в точках a и b и отрезком оси Ox между точками a и b. Поэтому, еслиf(x) меняет знак, то 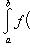
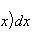 равен сумме взятых с определенным знаком площадей криволинейных трапеций, расположенных выше и ниже оси Ox, причем площади первых берутся со знаком +, а вторых со знаком -.
равен сумме взятых с определенным знаком площадей криволинейных трапеций, расположенных выше и ниже оси Ox, причем площади первых берутся со знаком +, а вторых со знаком -.
Площадь фигуры, ограниченной двумя графиками
Для нахождения площади фигуры ограниченной двумя графиками функций необходимо:
1. Задать первую функцию и построить ее график.
2. Задать вторую функцию и построить ее график.
3. Определить замкнутую область и точки пересечения графиков.
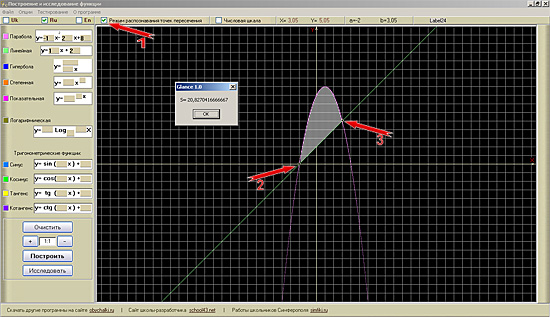
4. Отметить точки пересечения графиков кликом мыши в местах точек пересечения (2)(3), либо воспользоваться режимом распознавания точек пересечения (1). При включении этого режима в верхней панели программы и подведении курсора мыши к предполагаемой точке пересечения автоматически точка пересечения отметится кружочком (2), курсор отскочит и будет готов к отметке по такому же принципу второй точки (3).
5. После выявления двух точек пересечения графиков автоматически область, ограниченная двумя графиками, заштрихуется и на экране появится форма с вычисленной ее площадью.
Вычисление пути, пройденного телом
Пусть U(t) = f(t) – уравнение изменения скорости 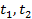 -начальное и конечное значение времени. Если точка движется со U =f(t), то её путь пройденный за промежуток времени от
-начальное и конечное значение времени. Если точка движется со U =f(t), то её путь пройденный за промежуток времени от 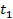 до
до 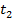 находиться по формуле
находиться по формуле 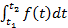 =
= 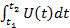
Длина дуги плоской кривой
