Определение суммы двух матриц, вычисление суммы.

Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Умножение матрицы на число.

Произведение двух матриц.

Определитель квадратной матрицы.

Определитель — одно из основных понятий линейной алгебры. Определитель матрицы является многочленомот элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Определение через разложение по первой строке

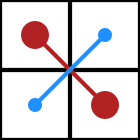
Схема расчета определителя матрицы .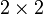

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

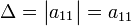
Для матрицы 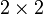детерминант определяется как

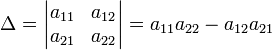
Для матрицы 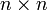определитель задаётся рекурсивно:

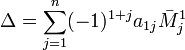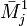, где — дополнительный минор к элементу 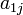. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы 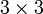такова:

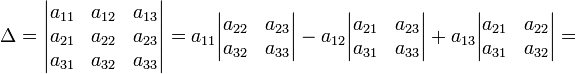
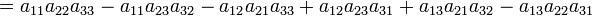
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

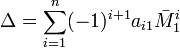
Доказательство

Также справедливо и аналогичное разложение по любой строке (столбцу):

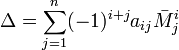
Доказательство Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

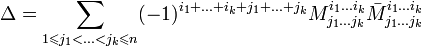
Определение через перестановки

Для матрицы 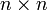справедлива формула:

,

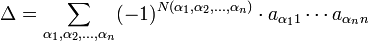где 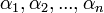— перестановка чисел от 1 до 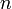, 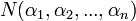— число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка 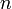. Таким образом, в определитель войдёт 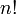слагаемых, которые также называют «членами определителя». Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.

Схема вычисления определителя третьего порядка.

Вычисление определителя по схеме.

Определитель третьего порядка вычисляется по формуле

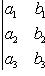
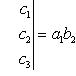
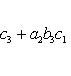
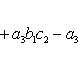
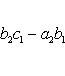
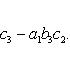(2)

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

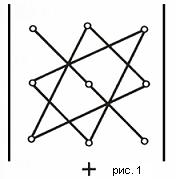
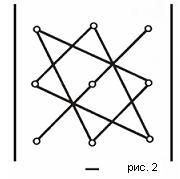
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений

Системы линейных уравнений.

Решение систем уравнений методом Крамера.

Решение систем уравнений методом Гаусса.

Основные правила дифференцирования функции, простейшие производные.

13. Производная сложной функции.