Температурное поле в процессе охлаждения (нагревания) бесконечно длинного цилиндра и шара.

Охлаждение (нагревание) тел, имеющих форму параллелепипеда или цилиндра конечных размеров.

Регулярный тепловой режим.

Для того чтобы ввести понятие регулярного теплового режима, рассмотрим процесс охлаждения (нагрева) в среде с постоянной температурой произвольного по форме однородного и изотропного тела, начальное распределение температур в котором в начальный момент времени τ = 0 задано известной функцией координат f(x, y, z,0)=T₀. В целях упрощения записи будем, не уменьшая общности, считать температуру окружающей среды T_f =const.

Уравнение теплопроводности в безразмерных переменных записывается как:

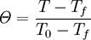
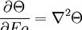, где — безразмерная температура, T = текущая температура тела T_f = температура среды, T₀ = начальная температура тела, Fo = Число Фурье.

Решением данного уравнения при изложенных выше условиях является ряд вида:

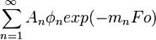
, где 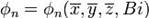(где Bi — число Био), а 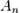зависит от начальных условий. Рассматривая поведение данного ряда с течением времени (то есть с ростом Fo), приходим к выводу, что

члены 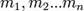убывают во времени, причем с неодинаковой скоростью. Члены высших порядков убывают быстрее и через некоторое время становятся пренебрежимо малы. Поэтому температура в любой точке тела задолго до достижения им температуры окружающей среды будет определяться, по существу, первым членом ряда, то есть

следовать простому экспоненциальному закону: .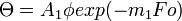

Момент, когда изменение температуры всех точек тела можно считать следующим этому простому закону, называют началом регулярного, то есть упорядоченного режима. В зависимости от характера изменения температуры окружающей среды T_f во времени различают регулярные режимы трёх родов.

Регулярный режим первого рода Рассмотренное выше условиеT_f=constопределяет регулярный режим первого рода.Признак регуляризации режима 1-го рода состоит в том, что изменение температуры в каждой точке системы происходит

по экспоненте, одинаковой для всех точек: , ,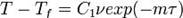

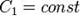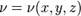где m — темп нагрева, который для малых чисел Био (Bi<<1) определяется как:

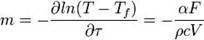
, где F — площадь поверхности тела, α — коэффициент теплоотдачи

ρ — плотность тела, c — теплоёмкость тела. Для произвольных Bi вводится коэффициент неравномерности температурного поля ψ, который можно определить как отношение средней по поверхности безразмерной температуры к средней безразмерной температуре по объёму. В предельном случае, когда число Био стремится к бесконечности, ψ=0

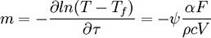
Тогда выражение для темпа нагрева принимает вид:

.[2]

Регулярный режим второго рода Наступает,когда скорость изменения температуры становится,во-первых,постоянной,

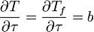
общей для всех точек тела, и, во-вторых, равной скорости изменения температуры внешней среды:

Регулярный режим третьего рода

Регулярный режим третьего рода реализуется в случае гармонических колебаний температуры среды около некоторой средней температуры.

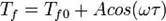
Xарактерно, что температура любой точки тела колеблется около своего среднего значения с тем же периодом, что и температура окружающей среды, то есть с периодом, одинаковым для всех точек тела:

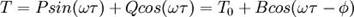где φ, T₀, P, Q, B — функции координат. (Очевидно, эти

колебания происходят с иной амплитудой, а также могут быть смещены по фазе по сравнению с колебаниями температуры окружающей среды.)