Температурное поле в процессе охлаждения (нагревания) пластины.

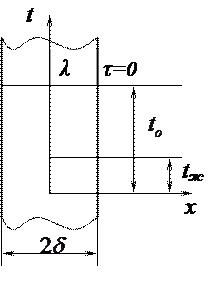
Постановка задачи. Пусть имеется пластина, размер которой вдоль оси х равен 2 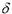. Размеры пластины в направлении осей y и z неограниченны, т.е. температура пластины изменяется только в направлении оси х. Пластина помещается в среду,

температура которой 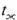= const. В начальный момент времени (t = 0) температура

в пластине распределена равномерно и равна 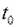, ( 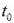> 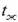), т.е. рассматриваем процесс охлаждения пластины. Все рассуждения и полученный результат будут верны и для процесса нагревания. Теплообмен с обеих поверхностей пластины одинаковый, коэффициент теплоотдачи a = const. В этом случае температурное поле будет симметричным относительно середины пластины. Теплоемкость и коэффициент теплопроводности материала пластины не зависят от температуры. Необходимо найти закон распределения температуры по толщине пластины и количество теплоты, отводимой с поверхности пластины, за любой промежуток времени. Обозначим избыточную температуру в любой точке тела в произвольный

момент времени через 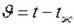. При t = 0 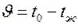. Для нахождения закона распределения температуры по толщине пластины в любой момент времени запишем дифференциальное уравнение теплопроводности, учитывая, что

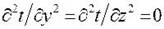. Согласно условию задачи уравнение

теплопроводности будет иметь вид

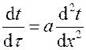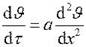или .Для решения этого уравнения воспользуемся методом разделения переменных.

Представим искомую функцию 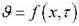в виде произведения T (t) и L (x): 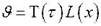Первый множитель зависит только от времени, а второй – только от координаты.

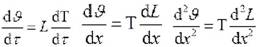
Дифференцируя выражение, найдем ; ; .

Подставим эти значения в решение, получим

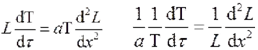или .Левая часть этого уравнения есть функция от времени (t ), а правая – от координаты (x). Значит, обе части должны быть равны некоторой постоянной величине, которую обозначим через (минус

).

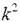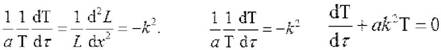
Тогда или ,

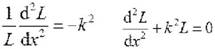
или . Это система обыкновенных дифференциальных уравнений, общие решения

которых известны:

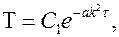
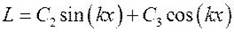. Общее решение будет иметь вид

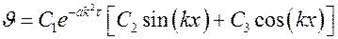
. Для нахождения частного решения необходимо определить

постоянные интегрирования ( 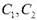и 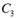), а также k. Для этого запишем начальные и граничные условия: при t = 0

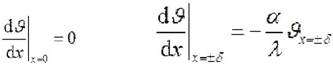
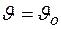; при x = 0 ; при x = ± d . Решая эту задачу,получаем уравнение

температурного поля в бесконечной пластине в виде

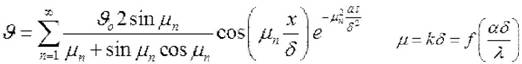
, где .

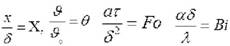
Запишем формулу в безразмерной форме. Обозначим , , – соответственно

безразмерные координата, температура, безразмерные числа Фурье и Био.

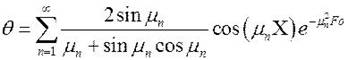
.Анализ формулы показывает, что чем больше номер ряда, тем меньшую долю вносит член в общую сумму ряда, т.е.

ряд быстро сходится, особенно при 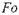³ 0,3. При этом распределение температуры достаточно точно описывается первым

членом ряда:

.

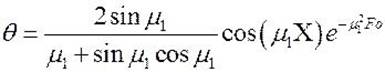
Пользование полученным уравнением на практике

затруднительно. Поэтому с помощью формулы построены

графики (номограммы). 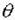= ¦(X, Fо, Bi), использование которых сводит расчеты к довольно простым операциям. Для практики часто бывает достаточно контролировать температуру тела в его центре или на поверхности и по изменению ее величины судить о процессе нагревания (охлаждения). Безразмерную температуру в центре пластины (x = 0, X = 0) можно определить по формуле

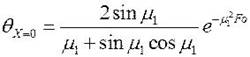
, а на поверхности пластины ( x = d , X = 1)

.

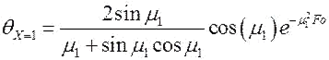Первые сомножители в этих выражениях зависят только от Bi. Обозначим их следующим образом:

,

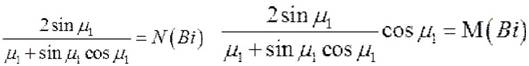
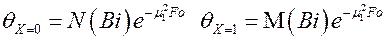
, тогда

,

. Прологарифмируем последние два выражения

, .

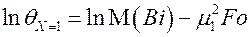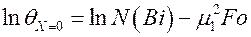
Графически эти зависимости представлены на номограммах. Пользуясь этими номограммами, можно легко найти температуру в центре и на поверхности бесконечной пластины (такие же номограммы имеются и для бесконечного цилиндра и шара) в любой момент времени. Для этого необходимо рассчитать безразмерные числа Bi и Fо и отложить их

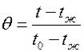
значения на соответствующей номограмме. Точка пересечения даст величину безразмерной температуры .

Зная 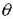, можно вычислить размерную температуру .

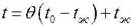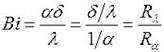
Физический смысл безразмерных чисел

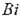и

.

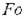характеризует соотношение между

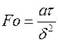
термическими сопротивлениями теплопроводности и теплоотдачи.

характеризует безразмерное время.