Теплопередача через плоскую стенку, расчет многослойных стенок.

Передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называется теплопередачей. Примером теплопередачи служит перенос теплоты от дымовых газов к воде через стенки труб парового котла, включающий в себя конвективную теплоотдачу от горячих дымовых газов к внешней стенке, теплопроводность в стенке и конвективную теплоотдачу от внутренней поверхности стенки к воде. Особенности протекания процесса на границах стенки при теплопередаче характеризуются граничными условиями третьего рода, которые задаются температурами жидкости с одной и другой стороны стенки, а также соответствующими значениями коэффициентов теплоотдачи.

Рассмотрим процесс теплопередачи через однородную плоскую стенку толщиной δ (рис. 12.1)

Заданы: коэффициент теплопроводности стенки λ, температуры окружающей среды t_ж1 и t_ж2, коэффициенты теплоотдачи α₁ и α₂. Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки t_с1 и t_с2. Плотность теплового потока от горячей среды к стенке определится уравнением (9.14)

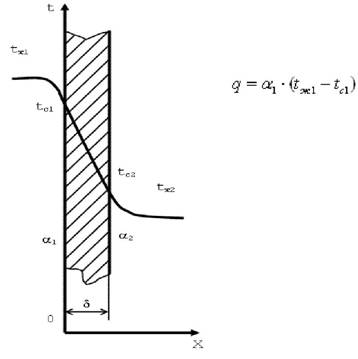
При стационарном режиме этот же тепловой поток пройдет путем теплопроводности через твердую стенку и будет передан от второй поверхности стенки к холодной среде за счет теплоотдачи:

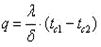
Перепишем приведенные уравнения в виде:

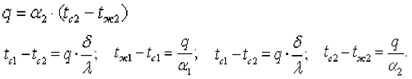
Складывая левые и правые части полученных равенств, запишем:

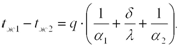
Отсюда

,

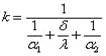
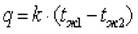Где ,

Величина k называется коэффициентом теплопередачи, который выражает количество теплоты, проходящее через единицу поверхности стенки в единицу времени при разности температур между горячей холодной и горячей жидкостью, равной 1К (размерность Вт/(м²·К)). Величина обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи.

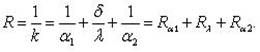
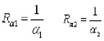
, Величины и называются термическими сопротивлениями теплоотдачи. Температуры на поверхностях однородной стенки

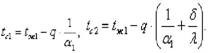
определяются из уравнений: [t1(x)=tc1+(tcл1-tcл2)/δ*x q=λ1/δ1(Tc1-Tcл1) q=λ2/δ2(Tcл1-Tcл2) q=λ3/δ3(Tcл2-Tc2)

q=Δt/( λ1/δ1+ λ2/δ2+ λ3/δ3)]

Стационарная теплопроводность цилиндрической стенки при граничных

Условиях первого рода.

Цилиндрические стенки встречаются на практике почти так же часто, как и плоские. Будем рассматривать неограниченные подлине стенки, у которых теплообменом с торцевых поверхностей можно пренебрегать и считать, что весь тепловой поток передается по направлениям, перпендикулярным оси цилиндра. С достаточной точностью к неограниченным можно относить любые стенки, длина которых хотя бы в 10 раз больше диаметра. При этом

изотермические поверхности представляют собою концентрические цилиндры, а в сечении, перпендикулярном оси этих цилиндров, изотермы имеют вид концентрических окружностей, как показано это на рис. 2.13. В декартовых координатах температурное поле является плоским t = f (х, у). Однако с переходом к цилиндрической системе координат в силу симметрии обнаруживается,что температура в любом месте стенки зависит лишь от одного параметра – радиуса r, определяющего положение этой точки на той или иной изотерме, т.е. задача становится одномерной: t = f (r).

Чтобы показать многообразие подходов при решении задач теплопроводности, отходя от общего подхода, покажем, что для тел простой формы задачу можно решить и без привлечения дифференциального уравнения теплопроводности. Выделим внутри стенки на расстоянии r от оси элементарно тонкий слой толщиной dr (см. рис. 2.14) и в соответствии с законом Фурье запишем формулу, определяющую величину передаваемого через этот слой теплового потока:

Q = Fq = 2πrl [–λ(dt/dr)]. У неограниченной стенки весь этот поток Q проходит целиком через любую изотермическуюповерхность, т.е. не зависит от величины r. Формула (2.18) представляет собою обыкновенное дифференциальное уравнение, описывающее связь между Q, r и t. Разнесем переменные и проинтегрируем затем правую и левую части

полученного уравнения в пределах, соответствующих граничным условиям: при r = r1 t = tc1 и при r = r2 t = tc2:

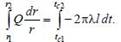
После интегрирования (с учетом, что Q = const) получаем Q ln (r2/r1) = –2πλl (tc2 – tc1), откуда находим:

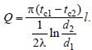, Чтобы определить вид температурного поля, повторим такое же интегрирование, но до некоторых текущих значений r и t верхних пределов:

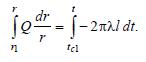
Тогда получим Q ln (r/r1) = –2πλl (t – tc1), откуда выражаем значение t :

Отметим, что удельные тепловые потоки на внутренней и на наружной поверхностях различны, поскольку различна величина этих поверхностей:

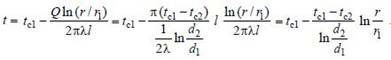
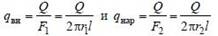, и это неудобно для практических расчетов. Поэтому вводится понятие о линейной плотности теплового потока ql: ql = Q / l, величина которой не зависит от радиуса. Связь между qнар, qвн и ql определяется из равенства qвн F1 = qнарF2 = ql1, откуда получаем ql = qвнF1 / l = qнарF2 / l = π d1 qвн = π d2 qнар .