Заполнение матрицы значениями функции в MathCAD

Рассмотрим решение на примере следующей задачи:

исследовать изменение значений

h=b+Vt-gt²/2

при изменении t от 10 до16 с шагом 2 с и при изменении высоты b от начального значения bn=3,4 м до конечного значения bk=6,9 м c шагом Db=70 см.

V=10 м/сек²

Зададим входные данные, присваивая переменным значения с единицами измерения

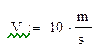
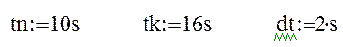
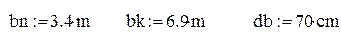
Определим функцию

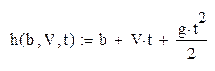
Константу g задавать не надо, так как она является встроенной в MathCAD.

Заполним вектор (одномерный массив) b значениями высоты

Число элементов m в векторе b можно вычислить по формуле

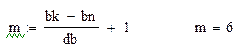
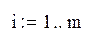
Введём ранжированную переменную

Для начала нумерации массива с единицы надо присвоить
переменной ORIGIN:=1

для i-того элемента вектора

тогда

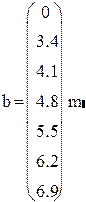
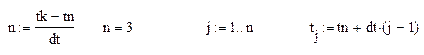
Так как в MathCAD вектор это один столбец для вывода в строку используем операцию транспонирования.

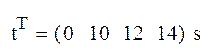
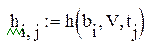
Тогда элемент таблицы (матрицы) равен

Полностью решение в MathCAD выглядит так:

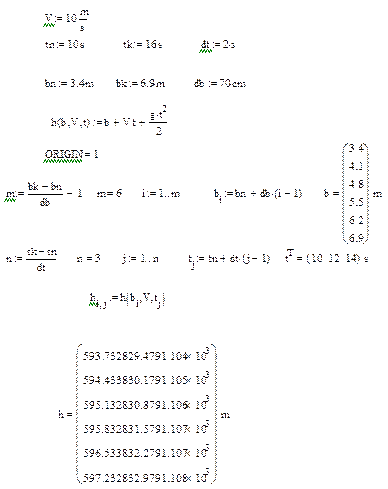
Задание к лабораторной работе № 2

Заполнить матрицу значениями функции :

F(x,y) = a*sin(Pi*x)*cos(Pi*y)

Значение константы а, диапазон изменения и шаг по переменным х и у выбрать самостоятельно.

ЗАДАНИЯ НА МАТРИЦЫ

1. Определить произведение матриц А и В (матрицу А взять из табл. 1.6., матрицу B задать произвольно).

2. Транспонировать матрицы А и В.

3. Ввести матрицу Н (из табл. 1.6.). Вычислить определитель 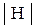и получить обратную матрицу .

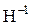4. Ввести вектор V (из табл. 1.6.). Определить сумму элементов вектора, максимальный элемент в нём. Упорядочить его элементы по возрастанию. Создать на основе вектора V диагональную матрицу.

Таблица 1.6.

Вариант	H	А	V

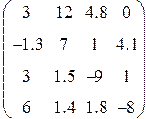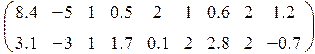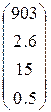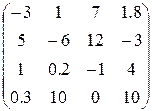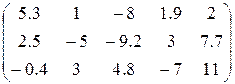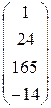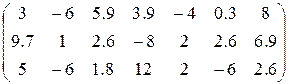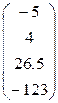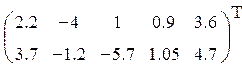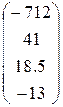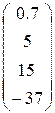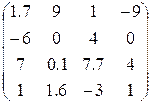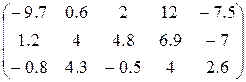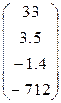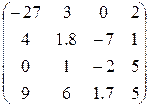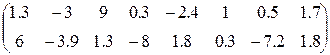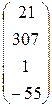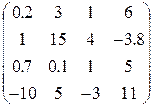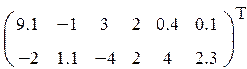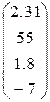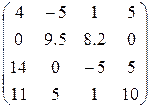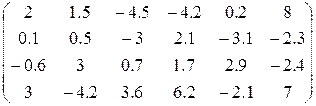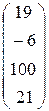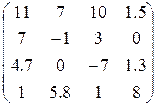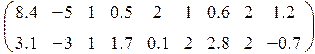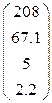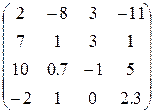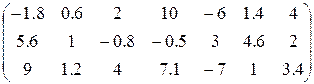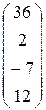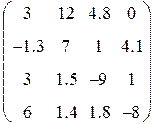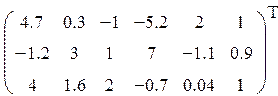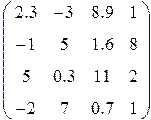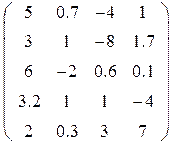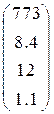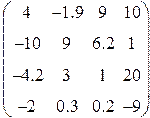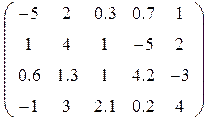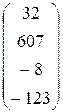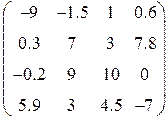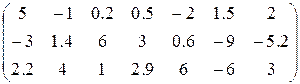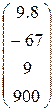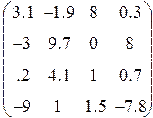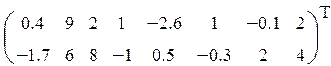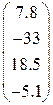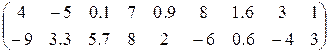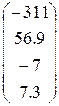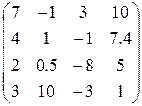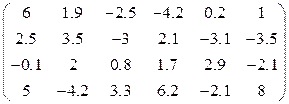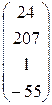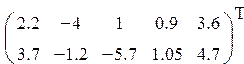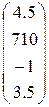ЛАБОРАТОРНАЯ РАБОТА №3

Решения СЛАУ . Реализовать решение заданной СЛАУ в среде MathCAD

Решение СЛАУ в среде MathCad

Mетод Крамера

Матричный метод

Решить СЛАУ методом матричным методом.

1. Проверка условия невырожденности матрицы A

1.

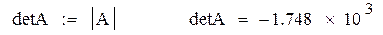
2. Определение вектора решения системы X

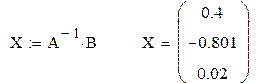
Метод итерации

Информация к решению

Метод итерации относится к разряду приближённых.

Рекомендуется использовать специальный вычислительный блокMathCAD:

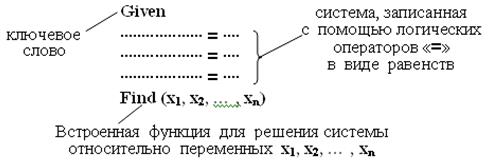
Знак логического оператора «=» можно ввести в документ с панели инструментов Математика => палитры Операторы или с помощью сочетания клавиш Ctrl+ =.

В качестве начальных (нулевых) приближений для искомых неизвестных:

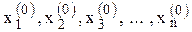
рекомендуется принимать соответствующие значения свободных членов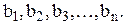

Решить СЛАУ (8) методом итерации.

1. Задание начальных (нулевых) приближений для искомых неизвестных:

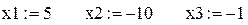
2. Нахождение решения системы (8)

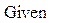
10·x1–x2+10·x3=5

15·x1+20·x2+ x3=–10

–2·x1–10·x3=–1

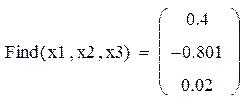
С помощью встроенной функции lsolve

Решить СЛАУ (8) с помощью встроенной функции lsolve.

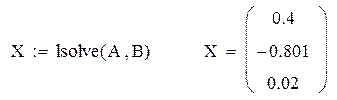
Задание к лабораторной работе № 3