Математические методы и средства решения

КУРСОВАЯ РАБОТА

по дисциплине ИНФОРМАТИКА

(наименование учебной дисциплины согласно учебному плану)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: Реализация численного метода средствами Microsoft Excel и математического

пакета MathCAD

Автор: студент гр. ТХО-14 /Гизатуллина К.Р./

(подпись) (Ф. И. О.)

ОЦЕНКА:

Дата:

ПРОВЕРИЛ:

Руководитель работы ассистент /Косарев О.В./

(должность) (подпись) (Ф. И. О.)

Санкт-Петербург

Санкт-Петербургский национальный минерально-сырьевой университет «Горный»

УТВЕРЖДАЮ

Заведующий кафедрой

//доцент Маховиков А.Б./

“”2015 г.

Кафедра: Информатики и компьютерных технологий

КУРСОВАЯ РАБОТА

По дисциплине: ИНФОРМАТИКА

^{(наименование учебной дисциплины согласно учебному плану)}

ЗАДАНИЕ

Студенту группы: ТХО-14Гизатуллиной К.Р.

^{(шифр группы) (Ф.И.О.)}

1. Тема работы: Реализация численного метода средствами Microsoft Excel

и математического пакета MathCAD

2. Исходные данные к работе: Вариант 1

3. Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы, расчетные формулы, расчеты с помощью электронных таблиц Microsoft Excel, расчеты с использованием пакета MathCAD, графическое решение, заключение, библиографический список

4. Перечень графического материала: 15 рисунков.

Срок сдачи законченной работы: 01.05.2015г.

Руководитель работы: ассистент /Косарев О.В./

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: 22.02.2015

Аннотация

Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по нахождению эмпирических формул методом наименьших квадратов (МНК) посредством табличного процессора Microsoft Excel, а также рассматривается решение данной задачи средствами математического пакета MathCAD. В работе получены уравнения различных видов с помощью аппроксимации линейной, квадратичной и экспоненциальной зависимостей. По окончании работы сделан вывод, каким методом задача решена лучше всего.

Страниц 30, таблиц 2, рисунков 15.

Abstract

Explanatory note is a report on the implementation of the course work . It addresses issues of finding empirical formulas by least squares (OLS ) by spreadsheet Microsoft Excel, as well as consider the solution of this problem by means of mathematical package MathCAD. We obtain the equations of various kinds by approximating linear, quadratic and exponential dependence . At the end of the conclusion , which method is best solved the problem .

Pages 30, tables 2, figures 15.

Оглавление

Введение. 5

1 Постановка задачи. 6

2 Математические методы и средства решения. 7

3 Исходные данные. 12

4.1 Аппроксимация функции с помощью Excel 13

4.2 Коэффициент корреляции. Коэффициенты детерминированности. 18

4.3 Графический способ в Excel 21

4.4 Аппроксимация функции с помощью MathCAD.. 24

Заключение. 29

Список использованной литературы.. 30

Введение

Аппроксимация (от латинского "approximate"- "приближаться") – приближенное описание эмпирических данных с помощью уравнений. Задача аппроксимации – найти такую функцию, выраженную аналитической формулой, чтобы она наилучшим образом описывала эмпирические данные. Для решения задачи аппроксимации наиболее часто используется метод наименьших квадратов, который позволяет найти функцию с такими параметрами, что сумма квадратов отклонений найденной функции от заданных значений функции будет минимальной.

Между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом.

При выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей. Для этого и применяется аппроксимация – приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее «тренд»). При выборе аппроксимации следует исходить из конкретной задачи исследования. Важно учитывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, многопараметрическое уравнение.

Цель данной курсовой работы – с помощью аппроксимации установить за- висимость между экспериментальными данными, решить поставленную задачу раз- личными способами, провести расчеты с помощью табличного процессора Microsoft Excel и математического пакета MathCad.

Постановка задачи

Во всех вариантах требуется:

1. Используя метод наименьших квадратов функцию 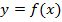заданную таблично, аппроксимировать:

а) многочленом первой степен ;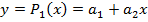

б) многочленом второй степени ;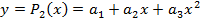

в) экспоненциальной зависимостью .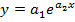

2. Для каждой зависимости вычислить коэффициент детерминированности.

3. Вычислить коэффициент корреляции (только в случае а).

4. Для каждой зависимости построить линию тренда.

5. Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует функцию .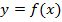

6. Выполнить обработку заданных экспериментальных данных с использованием встроенных функции интерполяции (аппроксимации) и регрессии пакета MathCAD и сравнить результаты с решение в Microsoft Excel.

Исходные данные

Задание

Функция 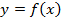задана таблицей 2:

Таблица 2 Исходные данные функции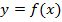

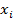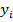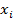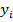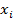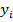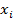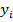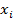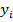0.51	4.57	3.33	15.11	4.87	20.87	7.44	32.15	9.87	41.82
1.11	6.22	3.39	16.03	5.35	23.83	7.98	33.32	10.65	43.76
1.62	8.99	3.51	16.51	5.94	26.18	8.87	37.84	10.76	45.36
2.65	13.09	3.99	18.42	6.87	26.76	8.90	37.96	11.03	45.97
2.74	13.45	4.42	20.13	7.12	30.88	9.54	42.65	11.76	49.34

Требуется выяснить – какая из функций – линейная, квадратичная или экспоненциальная наилучшим образом аппроксимирует функцию, заданную таблицей 2.

Графический способ в Excel

Представим графические результаты расчетов, полученные выше. Исследуем характер зависимости x и y в три этапа с помощью «Мастера диаграмм» в MS Excel:

1) Построить график зависимости

2) Построить линию тренда

3) Получить числовые характеристики коэффициентов уравнения.

1) Построение графика зависимости:

1. Выделяем интервал В2:В26.

2. Вызываем Мастер диаграмм, нажав соответствующую кнопку на панели инструментов.

3. Используя мышь, выделим область для встроенной диаграммы.

4. выбираем тип диаграммы – точечная.

5. Далее в окне «Название диаграммы» введем заголовок «Линейная аппроксимация»; в окне «Категория [Х]» введем «х», в окне «Значения [Y]» введем значения «y».

2) Построение линии тренда:

Для построения линии тренда выполним следующую последовательность действий:

1. Дважды щелкнем по диаграмме. Диаграмма активизируется.

2. Щелкнем по графику непосредственно в одну из изображенных точек, сам график активизируется его окраска измениться.

3. Вставляем линию тренда, воспользуемся меню Вставка/Линия тренда.

4. Выберем на вкладке «Тип» линейный тип и перейдем к вкладке «Параметры».

5. На вкладке “Параметры” потребуем показывать уравнение тренда на диаграмме и показывать значение 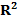. Нажмем кнопку ОК (рис. 9)[2].

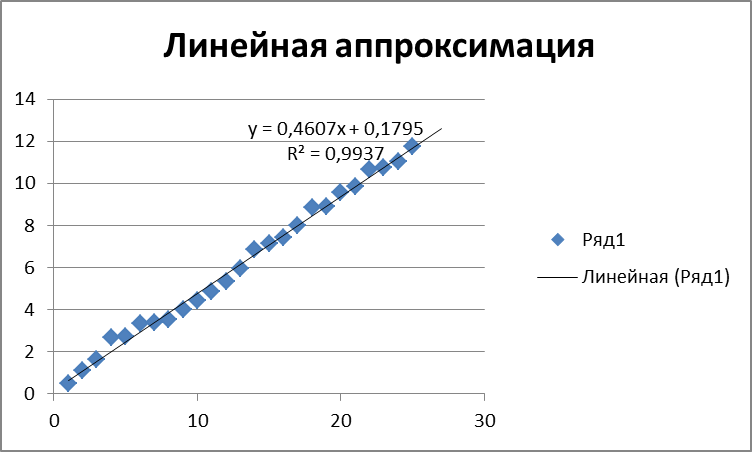
Рис. 9. График зависимости линии тренда для линейной аппроксимации

Для построения квадратичной аппроксимациина четвертом шаге в диалоговом окне “Линия тренда” выберем на вкладке “Тип” полиномиальный тип степень 2. Результат представлен на рис.10.

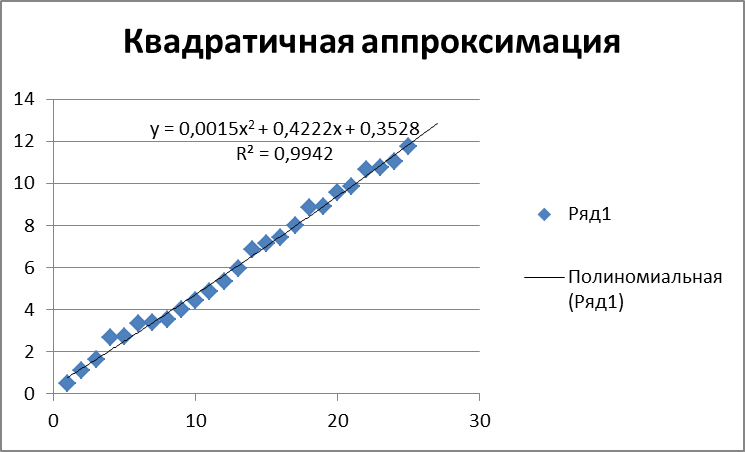
Рис 10. График зависимости линии тренда для квадратичной аппроксимации

Для построения экспоненциальной аппроксимации на четвертом шаге в диалоговом окне “Линия тренда” выберем на вкладке “Тип” экспоненциальный тип. Результат представлен на рис.11.

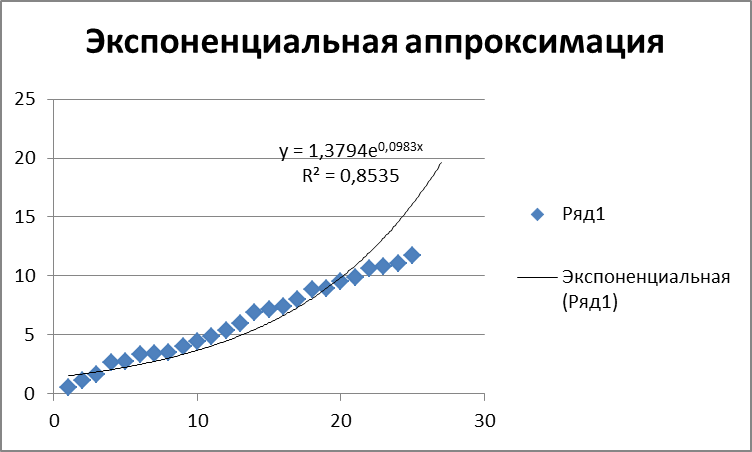
Рис. 11. График зависимости линии тренда для экспоненциальной аппроксимации

Построение линий тренда в MS Excel показало совпадение значений величин, полученных на графиках, с величинами, рассчитанными по формулам.

Линейная регрессия

Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями:

intercept(X,Y) – вычисляем параметр 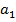, смещение линии регресси по вертикали;

slope(X,Y)– вычисляем параметр 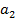, угловой коэффициент линии регрессии.

Полученные значения коэффициентов используем в уравнение регрессии .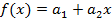

Функция Corr(Y,y(x)) – вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости [3].

Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x) (рис.13)

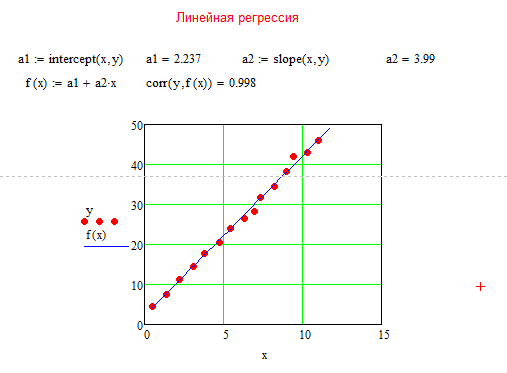
Рис. 13. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации

Уравнение линейной регрессии, полученное в MathCAD: y=2.237+3.99.

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты 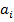полинома n-й степени.

Значения коэффициентов 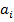могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0).

Полученные значения коэффициентов используем в уравнении регрессии .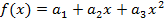

Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x) (рис. 14).

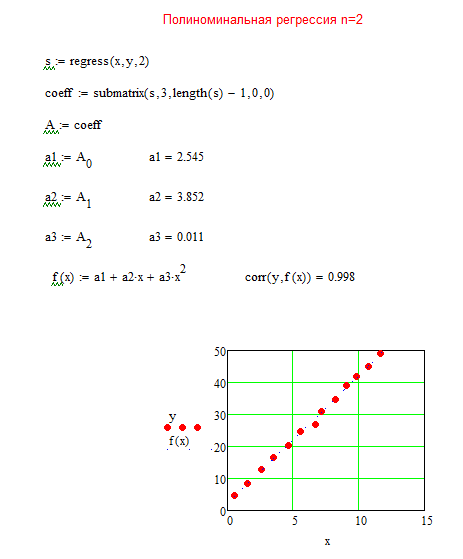
Рис.14. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для квадратичной аппроксимации

Уравнение полиномиальной регрессии : y=2.545+3.852х+0.011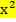

Экспоненциальная регрессия

Для определения экспоненциальной функции решим систему (10) в MathCAD:

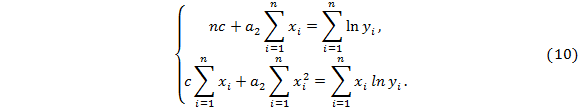
Для этого с помощью значков суммирования векторов 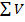и векторизации 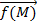, находящихся на панели векторов и матриц, вычисляем: 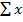, , 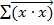, 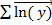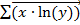(рис.15).

Затем составляем матрицы А и В из соответствующих коэффициентов системы линейных уравнений (10) и находим решение системы с помощью встроенной функции lsolve (см. рис. 15).

Решив систему (10), получим значения коэффициентов с и .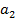

Коэффициент 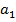вычисляем по формуле: 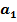=exp(с).

Полученные значения коэффициентов используем в уравнение регрессии .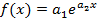

Вычислив параметры экспоненциальной регрессии, строим графики исходной функции y и функции экспоненциальной регрессии f(x) (рис. 15).

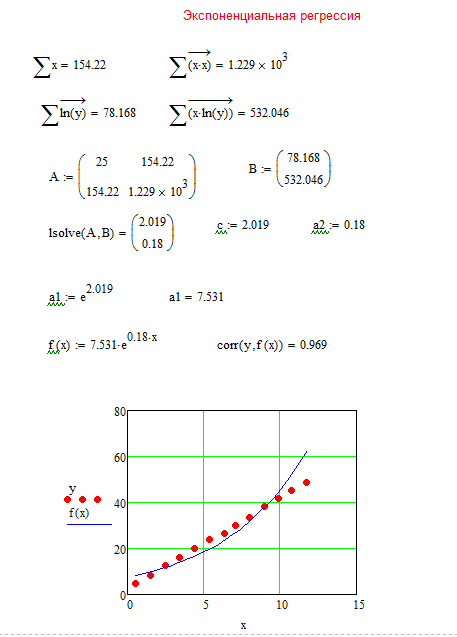
Рис. 15. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для экспоненциальной аппроксимации

Уравнение экспоненциальной регрессии: .

Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.

Заключение

Сделаем заключение по результатам полученных данных:

1. В ходе обработки исходных данных средствами функций MS Excel и MathCAD были получены три варианта уравнения аппроксимации: линейная, квадратичная и экспоненциальная.

2. Анализ результатов расчетов показывает, что линейная аппроксимация наилучшим образом описывает экспериментальные данные, так как имеет самый высокий коэффициент детерминированности (0,9960).

Уравнение линейной аппроксимации имеет следующий вид: y=2.237+3.99

3. Совпадение значений величин, полученных на графиках и рассчитанных по формулам в MS Excel, говорит о правильности вычислений.

4. Результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel. Это говорит о верности вычислений.

Список использованной литературы

1. Бердышев В.И., Петрак Л.В. Аппроксимация функций, сжатие численной информации, приложения. – Екатеринбург: УрО РАН, 1999. – 296 с.

2. Малинина Л.А. Основы информатики: Учебник для вузов. – Ростов н/Д.: Феникс, 2006. – 352 с.

3. Макаров Е.Г. MathCAD: Учебный курс. – СПб.: Питер, 2009. – 384 с.

КУРСОВАЯ РАБОТА

по дисциплине ИНФОРМАТИКА

(наименование учебной дисциплины согласно учебному плану)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: Реализация численного метода средствами Microsoft Excel и математического

пакета MathCAD

Автор: студент гр. ТХО-14 /Гизатуллина К.Р./

(подпись) (Ф. И. О.)

ОЦЕНКА:

Дата:

ПРОВЕРИЛ:

Руководитель работы ассистент /Косарев О.В./

(должность) (подпись) (Ф. И. О.)

Санкт-Петербург

Санкт-Петербургский национальный минерально-сырьевой университет «Горный»

УТВЕРЖДАЮ

Заведующий кафедрой

//доцент Маховиков А.Б./

“”2015 г.

Кафедра: Информатики и компьютерных технологий

КУРСОВАЯ РАБОТА

По дисциплине: ИНФОРМАТИКА

^{(наименование учебной дисциплины согласно учебному плану)}

ЗАДАНИЕ

Студенту группы: ТХО-14Гизатуллиной К.Р.

^{(шифр группы) (Ф.И.О.)}

1. Тема работы: Реализация численного метода средствами Microsoft Excel

и математического пакета MathCAD

2. Исходные данные к работе: Вариант 1

3. Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы, расчетные формулы, расчеты с помощью электронных таблиц Microsoft Excel, расчеты с использованием пакета MathCAD, графическое решение, заключение, библиографический список

4. Перечень графического материала: 15 рисунков.

Срок сдачи законченной работы: 01.05.2015г.

Руководитель работы: ассистент /Косарев О.В./

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: 22.02.2015

Аннотация

Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по нахождению эмпирических формул методом наименьших квадратов (МНК) посредством табличного процессора Microsoft Excel, а также рассматривается решение данной задачи средствами математического пакета MathCAD. В работе получены уравнения различных видов с помощью аппроксимации линейной, квадратичной и экспоненциальной зависимостей. По окончании работы сделан вывод, каким методом задача решена лучше всего.

Страниц 30, таблиц 2, рисунков 15.

Abstract

Explanatory note is a report on the implementation of the course work . It addresses issues of finding empirical formulas by least squares (OLS ) by spreadsheet Microsoft Excel, as well as consider the solution of this problem by means of mathematical package MathCAD. We obtain the equations of various kinds by approximating linear, quadratic and exponential dependence . At the end of the conclusion , which method is best solved the problem .

Pages 30, tables 2, figures 15.

Оглавление

Введение. 5

1 Постановка задачи. 6

2 Математические методы и средства решения. 7

3 Исходные данные. 12

4.1 Аппроксимация функции с помощью Excel 13

4.2 Коэффициент корреляции. Коэффициенты детерминированности. 18

4.3 Графический способ в Excel 21

4.4 Аппроксимация функции с помощью MathCAD.. 24

Заключение. 29

Список использованной литературы.. 30

Введение

Аппроксимация (от латинского "approximate"- "приближаться") – приближенное описание эмпирических данных с помощью уравнений. Задача аппроксимации – найти такую функцию, выраженную аналитической формулой, чтобы она наилучшим образом описывала эмпирические данные. Для решения задачи аппроксимации наиболее часто используется метод наименьших квадратов, который позволяет найти функцию с такими параметрами, что сумма квадратов отклонений найденной функции от заданных значений функции будет минимальной.

Между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом.

При выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей. Для этого и применяется аппроксимация – приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее «тренд»). При выборе аппроксимации следует исходить из конкретной задачи исследования. Важно учитывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, многопараметрическое уравнение.

Цель данной курсовой работы – с помощью аппроксимации установить за- висимость между экспериментальными данными, решить поставленную задачу раз- личными способами, провести расчеты с помощью табличного процессора Microsoft Excel и математического пакета MathCad.

Постановка задачи

Во всех вариантах требуется:

1. Используя метод наименьших квадратов функцию 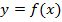заданную таблично, аппроксимировать:

а) многочленом первой степен ;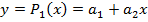

б) многочленом второй степени ;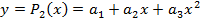

в) экспоненциальной зависимостью .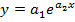

2. Для каждой зависимости вычислить коэффициент детерминированности.

3. Вычислить коэффициент корреляции (только в случае а).

4. Для каждой зависимости построить линию тренда.

5. Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует функцию .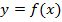

6. Выполнить обработку заданных экспериментальных данных с использованием встроенных функции интерполяции (аппроксимации) и регрессии пакета MathCAD и сравнить результаты с решение в Microsoft Excel.

Математические методы и средства решения