Лекция 4. Структурный синтез. Синтез автоматизированных систем. Входные и выходные параметры моделей

Разработка (или выбор) структуры объекта есть проектная процедура, называемая структурным синтезом, а расчет (или выбор) значений параметров элементов Х- процедура параметрического синтеза.

Задача структурного синтеза формулируется в системотехнике как задача принятия решений (ЗПР). Ее суть заключается в определении цели, множества возможных решений и ограничивающих условий.

Классификацию ЗПР осуществляют по ряду признаков. По числу критериев различают задачи одно- и многокритериальные. По степени неопределенности различают ЗПР детерминированные, ЗПР в условиях риска - при наличии в формулировке задачи случайных параметров, ЗПР в условиях неопределенности, т.е. при неполноте или недостоверности исходной информации.

Реальные задачи проектирования, как правило, являются многокритериальными. Одна из основных проблем постановки многокритериальных задач - установление правил предпочтения вариантов. Способы сведения многокритериальных задач к однокритериальным и последующие пути решения изучаются в дисциплинах, посвященных методам оптимизации и математическому программированию.

Наличие случайных факторов усложняет решение ЗПР. Основные подходы к решению ЗПР в условиях риска заключаются или в решении «для наихудшего случая», или в учете в целевой функции математического ожидания и дисперсии выходных параметров. В первом случае задачу решают как детерминированную при завышенных требованиях к качеству решения, что является главным недостатком подхода. Во втором случае достоверность результатов решения намного выше, но возникают трудности с оценкой целевой функции. Применение метода Монте-Карло в случае алгоритмических моделей становится единственной альтернативой и, следовательно, для решения требуются значительные вычислительные ресурсы.

Существуют две группы ЗПР в условиях неопределенности. Одна из них решается при наличии противодействия разумного противника. Такие задачи изучаются в теории игр, для задач проектирования в технике они не характерны. Во второй группе достижению цели противодействие оказывают силы природы. Для их решения полезно использовать теорию и методы нечетких множеств.

Например, при синтезе структуры автоматизированной системы постановка задачи должна включать в качестве исходных данных следующие сведения:

- множество выполняемых системой функций (другими словами, множество работ, каждая из которых может состоять из одной или более операций); возможно, что в этом множестве имеется частичная упорядоченность работ, что может быть представлено в виде ориентированного графа, в котором вершины соответствуют работам, а дуги - отношениям порядка;

- типы допустимых для использования серверов (машин), выполняющих функции системы;

- множество внешних источников и потребителей информации;

- во многих случаях задается также некоторая исходная структура системы в виде взаимосвязанной совокупности серверов определенных типов; эта структура может рассматриваться как обобщенная избыточная или как вариант первого приближения;

- различного рода ограничения, в частности, ограничения на затраты материальных ресурсов и (или) на времена выполнения функций системы.

Задача заключается в синтезе (или коррекции) структуры, определении типов серверов (программно-аппаратных средств), распределении функций по серверам таким образом, чтобы достигался экстремум целевой функции при выполнении заданных ограничений.

Конструирование, разработка технологических процессов, оформление проектной документации - частные случаи структурного синтеза.

Задачу параметрического синтеза называют параметрической оптимизацией (или оптимизацией), если ее решают как задачу математического программирования

extrF(X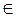), X D_x,

где F(X) - целевая функция; X- вектор управляемых (называемых также проектными или варьируемыми) параметров; D_x = {X| ϕ(X) < 0, ψ(X) = 0} - допустимая область; ϕ(X) и ψ(X) - функции-ограничения.

Следующая после синтеза группа проектных процедур - процедуры анализа. Цель анализа - получение информации о характере функционирования и значениях выходных параметров Yпри заданных структуре объекта, сведениях о внешних параметрах Qи параметрах элементов Х. Если заданы фиксированные значения параметров Хи Q,то имеет место процедура одновариантного анализа, которая сводится к решению уравнений математической модели, например, такой, как модель (1.1), и вычислению вектора выходных параметров Y. Если заданы статистические сведения о параметрах Х и нужно получить оценки числовых характеристик распределений выходных параметров (например, оценки математических ожиданий и дисперсий), то это процедура статистического анализа. Если требуется рассчитать матрицы абсолютной Аи (или) относительной Вчувствительности, то имеет место задача анализа чувствительности.

Элемент А_ji матрицы Аназывают абсолютным коэффициентом чувствительности, он представляет собой частную производную j-го выходного параметра yj по i-ому параметру xi. Другими словами, А_ji является элементом вектора градиента j-го выходного параметра. На практике удобнее использовать безразмерные относительные коэффициенты чувствительности B_ji, характеризующие степень влияния изменений параметров элементов на изменения выходных параметров:

B_ji = A_ji x_iном / y_jном,

где x_iном и y_jном - номинальные значения параметров x_i и y_j соответственно.

В процедурах многовариантного анализа определяется влияние внешних параметров, разброса и нестабильности параметров элементов на выходные параметры. Процедуры статистического анализа и анализа чувствительности - характерные примеры процедур многовариантного анализа.

Контрольные вопросы

1. Что называют структурным синтезом?

2. Назовите исходные данные при синтезе автоматизированной системы?

3. Какова цель процедуры анализа?

4. Какова основная проблема постановки многокритериальных задач?

Лекция 5. Математическое обеспечение. Требования к математическим моделям. Маршруты проектирования

К математическому обеспечению (МО) анализа относят математические модели, численные методы, алгоритмы выполнения проектных процедур. Компоненты МО определяются базовым математическим аппаратом, специфичным для каждого из иерархических уровней проектирования.

На микроуровне типичные математические модели (ММ) представлены дифференциальными уравнениями в частных производных (ДУЧП) вместе с краевыми условиями. К этим моделям, называемым распределенными, относятся многие уравнения математической физики. Объектами исследования здесь являются поля физических величин, что требуется при анализе прочности строительных сооружений или машиностроительных деталей, исследовании процессов в жидких средах, моделировании концентраций и потоков частиц и т.п.

Число совместно исследуемых различных сред (число деталей, слоев материала, фаз агрегатного состояния) в практически используемых моделях микроуровня не может быть большим из-за сложностей вычислительного характера. Резко снизить вычислительные затраты в многокомпонентных средах можно, только применив иной подход к моделированию, основанный на принятии определенных допущений.

Допущение, выражаемое дискретизацией пространства, позволяет перейти к моделям макроуровня. Моделями макроуровня, называемыми также сосредоточенными, являются системы алгебраических и обыкновенных дифференциальных уравнений, поскольку независимой переменной здесь остается только время t. Упрощение описания отдельных компонентов (деталей) позволяет исследовать модели процессов в устройствах, приборах, механических узлах, число компонентов в которых может доходить до нескольких тысяч.

В тех случаях, когда число компонентов в исследуемой системе превышает некоторый порог, сложность модели системы на макроуровне вновь становится чрезмерной. Поэтому, принимая соответствующие допущения, переходят на функционально-логический уровень. На этом уровне используют аппарат передаточных функций для исследования аналоговых (непрерывных) процессов или аппарат математической логики и конечных автоматов, если объектом исследования является дискретный процесс, т.е. процесс с дискретным множеством состояний.

Наконец, для исследования еще более сложных объектов, примерами которых могут служить производственные предприятия и их объединения, вычислительные системы и сети, социальные системы и другие подобные объекты, применяют аппарат теории массового обслуживания, возможно использование и некоторых других подходов, например, сетей Петри. Эти модели относятся к системному уровню моделирования.

Основными требованиями к математическим моделям являются требования адекватности, точности, экономичности.

Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность имеет место, если модель отражает заданные свойства объекта с приемлемой точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели.

Экономичность (вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, далее речь пойдет о характеристиках именно математических моделей, и экономичность будет характеризоваться затратами машинных времени и памяти.

Адекватность оценивается перечнем отражаемых свойств и областями адекватности. Область адекватности – область в пространстве параметров, в пределах которой погрешности модели остаются в допустимых пределах. Например, область адекватности линеаризованной модели поверхности детали определяется системой неравенств:

max |ε_ij| ≤ ε_доп,

где ε_ij и ε_доп — допущенная и предельно допустимая относительные погрешности моделирования поверхности, максимум берется по всем координатам и контролируемым точкам.

Отметим, что в большинстве случаев области адекватности строятся в пространстве внешних переменных. Так, область адекватности модели электрического элемента обычно выражает допустимые для применения модели диапазоны изменения моделируемых температур, внешних напряжений, токовой нагрузки, частот.

Аналогичные требования по точности и экономичности фигурируют при выборе численных методов решения уравнений модели.

Вычислительный процесс при анализе состоит из этапов формирования модели и ее исследования (решения). В свою очередь, формирование модели включает две процедуры: во-первых, разработку моделей отдельных компонентов, во-вторых, формирование модели системы из моделей компонентов.

Первая из этих процедур выполняется предварительно по отношению к типовым компонентам вне маршрута проектирования конкретных объектов. Как правило, модели компонентов разрабатываются специалистами в прикладных областях, причем знающими требования к моделям и формам их представления в САПР. Обычно в помощь разработчику моделей в САПР предлагаются методики и вспомогательные средства, например, в виде программ анализа для экспериментальной отработки моделей. Созданные модели включаются в библиотеки моделей прикладных программ анализа.

На маршруте проектирования каждого нового объекта выполняется вторая процедура (рис.2) - формирование модели системы с использованием библиотечных моделей компонентов. Как правило, эта процедура выполняется автоматически по алгоритмам, включенным в заранее разработанные программы анализа.

При применении этих программ пользователь описывает исследуемый объект на входном языке программы анализа не в виде системы уравнений, которая будет получена автоматически, а в виде списка элементов структуры, эквивалентной схемы, эскиза или чертежа конструкции.

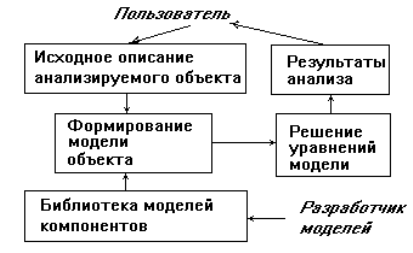
Рис 2. Место процедур формирования моделей на маршрутах проектирования

Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели.

Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.

Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов (ММЭ).

Топологические уравнения описывают взаимосвязи в составе моделируемой системы.

В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).

Компонентные уравнения имеют вид:

Fк (dV/dt, V, t) = 0

и топологические уравнения

Fт (V) = 0,

где V= (v1, v2, ...vn) - вектор фазовых переменных, t - время.

Различают фазовые переменные двух типов, их обобщенные наименования - фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение - связи между однотипными фазовыми переменными в разных компонентах.

Контрольные вопросы

1. Что относят к математическому обеспечению?

2. Какие основные требования предъявляются к математическим моделям?

3. Что понимают под адекватностью математической модели?

4. Что понимают под экономичностью математической модели?

5. Какие уравнения называют компонентными?

6. Какие уравнения называют топологическими?

7. Для чего используют компонентные уравнения?