Тригонометрические функции половинного аргумента

4.10 Преобразование суммы и разности тригонометрических функций в произведение

sinα + sinβ = 2∙sin ∙ cos

sinα - sinβ = 2∙sin ∙ cos

cosα + cosβ = 2∙cos ∙ cos

cosα - cosβ = - 2∙sin ∙ sin

4.11 Функция у=sinх

Основные свойства:

1) Область определения – множество R всех действительных чисел;

2) Множество значений – отрезок[-1;1];

3) Функция у=sinх – периодическая с периодом 2π, т.е. sin(х+2π)=sinх

4) Функция у=sinх - нечётная, т.е.sin(-х)=-sinх

5) Функция у=sinх:

возрастает на отрезках

убывает на отрезках

6) Функция у=sinх принимает

Наибольшее значение, равное 1, при х=

Наименьшее значение, равное –1, при х=-

Значение равное нулю, при х=

4.12 Функция у=cosх

Основные свойства:

1) Область определения – множество R всех действительных чисел;

2) Множество значений – отрезок[-1;1];

3) Функция у=cosх – периодическая с периодом 2π, т.е. cos(х+2π)=cosх

4) Функция у=cosх чётная, т.е.cos(-х)=cosх

5) Функция у=cosх:

возрастает на отрезках

убывает на отрезках

6) Функция у=cosх принимает

Наибольшее значение, равное 1, при х=

Наименьшее значение, равное –1, при х=

Значение равное нулю, при х=

4.13 Функция у=tgх

Основные свойства:

1) Область определения – множество R всех действительных чисел, кроме чисел ;

2) Множество значений – множество R всех действительных чисел;

3) Функция у=tgх – периодическая с периодом π, т.е. tg(х+2π)=tgх

4) Функция у=tgх нечётная, т.е.tg(-х)=-tgх

5) Функция у=tgх возрастает на интервалах

6) Функция у=tgх принимает значение равное нулю, при х=

2. Примеры и упражнения

Пример 1: Найти значение выражения:

1)3sin +2cos -tg =3∙ +2∙ - = - =

= + - =

2)3cos180º+5ctg270º-2sin360º=3∙(-1)+5∙0-2∙1=

= -3+0-2=-5

3)2sin(-30º)=-2sin30º=-2∙ =-1

4)4cos(- )∙sin(- )+tg(- )=4∙ ∙ )+(-1)=

=- ∙ -1=-3-1=4

5)Sin73º∙cos17º + cos73º∙sin17º= sin(73º +17º)=

=sin90º=1

6)cos ∙cos - sin ∙sin =

cos( + )=cos =cos2π=1

7)2∙sin15º∙cos15º= Sin2∙15º= Sin30º=

8)cos²75º - sin²75º= Cos2∙75º= Cos150º=-

9)Cos105º+cos75º=2∙cos ∙ cos =

= 2∙cos 15º ∙ cos 90º= 2∙cos 15º ∙ 0=0

10)Sin300º + sin60º=2∙sin ∙ cos = 2∙sin 180º ∙ cos120º=2∙0∙ cos120º=0

Пример 2:Вычислить cosα,tgα,ctgα, если sinα= ,

Решение:

Определим знак:

интервал	четверть	Знак sinα	Знак cosα	Знак tgα	Знак ctgα
	IIч.	+	-	-	-

Формула 1б)

Формула 2) Формула 3)

tgα= ctgα=

Ответ: cosα= ,tgα=- ,ctgα=

Пример 3:Вычислить sinα,cosα,tgα, , если ctgα=-3,

Решение:

Определим знак:

интервал	четверть	Знак sinα	Знак cosα	Знак tgα	Знак ctgα
	IVч.	-	+	-	-

Формула 4а)

Формула 5а)

Формула 6а)

Ответ: sinα=- , cosα= ,tgα=-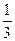

Пример 4: Упростить

1)(1-sinα)∙(1+sinα)=1+sinα-sinα-sin²α=1-sin²α=sin²α+cos²α-sin²α=cos²α

2) =1+tg²α-1=tg²α

3)

4)Sin(-α)∙cos(-α)∙tg(-α)=-sinα∙cosα∙(-tgα)=sinα∙cosα∙tgα=

=sinα∙cosα∙ =sinα∙sinα=sin²α

5)(1-sin(-α))∙(1-sinα)=(1+sinα)∙(1-sinα)=

=1+sinα-sinα-sin²α==1-sin²α=

=sin²α+cos²α-sin²α=cos²α

6)Sin(π – α)∙cos( -α)-cos(π – α)∙sin( -α)=

sinα∙sinα-(-cosα)∙cosα== sin²α+cos²α=1

7)

Варианты контрольной работы

Задание 1: Найти значение выражения

Вариант 1:

1) 12cos2π -16sinπ+13cos0-14sin

2) sin155º-sin25º

Вариант 2:

1) 9sinπ+10cos2π-11sin +12cos0

2) 2sin75º∙cos75º

Вариант 3:

1) 3sin²120º-4cos180º+3tg135º

2) sin20º∙cos10º+ cos20º∙ sin10º

Вариант 4:

1) 2cos²150º-3sin90º-5ctg135º

2) cos100º+cos80º

Вариант 5:

1)

2) cos²135º-sin²135º

Вариант 6:

1)

2) cos20º∙cos40º- sin20º∙ sin40º

Вариант 7:

1)

2) 2

Вариант 8:

1)

2)

Вариант 9:

1) cos60º+2sin30º+ tg²60º-ctg45º

2) cos100º+cos80º

Вариант 10:

1) 3cos²180º+5ctg270º-2sin360º-tg60º

2) sin155º-sin25º

Вариант 11:

1) cos +tg - sin

2) cos ∙cos + sin ∙sin

Вариант 12:

1) 2cos60º-tg45º

2) Sin73º∙cos17º - cos73º∙sin17º

Вариант 13:

1) 2tg45º+5ctg270º-3sin180º

2) Sin105º - sin75º

Вариант14:

1) 4ctg(-45º)∙sin(-30º)∙cos(- )

2) Cos105º + cos165º

Вариант 15:

1) 2cos 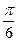+4sin -3ctg

2) 2sin ∙cos

Вариант 16:

1) 6cos(-2π)∙sin(- 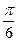)∙tg(-45º)

2) cos² - sin²

Вариант 17:

1) 3sin +2cos -tg

2) Sin40º∙cos5+cos40º∙sin5º

Вариант 18:

1) Sin -cos +14tg2π

2) Cos7º∙cos38º-sin7º∙sin38º

Вариант19:

1) tg ∙cos ∙sin

2) cos18º∙cos12º-sin18º∙sin12º

Вариант 20

1) 2sin60º+8cos30º-12ctg30º+8tg60º

2) sin20º∙sin40º -cos20º∙cos40º

Вариант 21:

1) 3sin²30º+5cos180º-6tg135º

2) Sin5º∙cos35º-cos5º∙sin35º

Вариант 22:

1) 4cos²60º-6cos360º+3tg²30º

2) Sin80º∙cos105º+cos80º∙sin10º

Вариант 23:

1) 2cos + 4sin -3ctg

2) Sin55º∙sin10º +cos55º∙cos10º

Вариант 24:

1) 13sin180º+5tg270º-2sin360º

2) Sin ∙cos +cos ∙sin

Вариант 25:

1)

2) cos20º∙cos40º-sin20º∙sin40º

Вариант 26:

1)

2) sin20º∙cos10º+cos20º∙sin10º

Вариант 27:

1)

2) sin155º-sin25º

Вариант 28:

1) 2tg(-45º)∙cos(-30º)∙sin(- )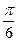

2) cos100º+cos80º

Вариант 29:

1) sin +4cos -3ctg

2) Cos105º + cos165º

Вариант 30:

1) 5cos(-π)∙cos(- )∙ctg(-45º)

2) Sin105º - sin75º

Задание 2: Найти остальные тригонометрические функции

Вариант 1:

1) sinα=-0,6

2) tgα=6

Вариант 2:

1) cosα=-

2) сtgα=9

Вариант 3:

1) sinα= , 0<α<

2) tgα=4, <α<π

Вариант 4:

1) cosα=- ,π<α<

2) ctgα=5, <α<π

Вариант 5:

1) sinα=-0,8,

2) tgα=5

Вариант 6:

1)

2)

Вариант 7:

1)

2)

Вариант 8:

1) sinα=-0,8 , <α<π

2) tgα=8, 0<α<

Вариант 9:

1) cosα=- ,π<α<

2) ctgα=2, <α<π

Вариант 10:

1) sinα=- ,

2) ctgα=-3,

Вариант 11:

1) sinα=0,6

2) tgα=4

Вариант 12:

1) cosα=-0,6,

2) ctgα=5, <α<π

Вариант 13:

1) cosα=-

2) ctgα=9, <α<π

Вариант14:

1) sinα= , 0<α<

2) ctgα=12, <α<π

Вариант 15:

1) cosα=-0,6, <α<π

2) tgα=13, <α<π

Вариант 16:

1) cosα=- , π<α<

2) tgα=15, <α<π

Вариант 17:

1) cosα=-

2) сtgα=9

Вариант 18:

1) sinα= , 0<α<

2) tgα=4, <α<π

Вариант 19:

1) cosα=- ,π<α<

2) ctgα=5, <α<π

Вариант 20:

1) sinα=-0,8,

2) tgα=5

Вариант 21:

1) sinα= , 0<α<

2) ctgα=12, <α<π

Вариант 22:

1) sinα=- ,

2) ctgα=-3,

Вариант 23:

1) cosα=- ,π<α<

2) ctgα=2, <α<π

Вариант 24:

1)

2)

Вариант 25:

1) sinα=-0,8 , <α<π

2) tgα=8, 0<α<

Вариант 26:

1)

2)

Вариант 27:

1) sinα=0,6

2) tgα=4

Вариант 28:

1) cosα=- , π<α<

2) tgα=15, <α<π

Вариант 29:

1) cosα=-0,6,

2) ctgα=5, <α<π

Вариант 30:

1) cosα=-

2) ctgα=9, <α<π

Задание 3: Упростить выражение

Вариант 1:

Вариант 2:

Вариант 3:

Вариант 4:

Вариант 5:

Вариант 6: sin²α-tgα∙ctgα+ cos²α

Вариант 7: (tgα∙ctgα+ ctg²α)∙cosα

Вариант 8:

Вариант 9: (tgα∙ctgα+ tg²α)∙sinα

Вариант 10:

Вариант 11:

Вариант 12: (1-sin²α)∙(1+tg²α)

Вариант 13:

Вариант14: (sin²α+cos²α)²-1

Вариант 15:1+sin(π+α)∙cos( +α)

Вариант 16:

Вариант 17: sinα∙cosα∙(tgα+ctgα)

Вариант 18:

Вариант19:

Вариант 20: +tgα∙ctgα

Вариант 21:

Вариант 22:

Вариант 23:

Вариант 24:

Вариант 25:

Вариант 26:

Вариант 27: Cos²α+sin²α-ctg²α

Вариант 28:

Вариант 29: 1+tg²α+

Вариант 30: (1-cosα)∙(1+cosα)

Содержание темы «Тригонометрические уравнения»

Арксинус числа

Определение арксинуса

Уравнение sinх = а

Формулы корней, особую форму записи решений для частных случаев

Арккосинус числа

Определение арккосинуса

Уравнение cosх = а

Формулы корней, особую форму записи решений для частных случаев

Арктангенс числа, арккотангенс числа. Уравнения tgх = а, ctgх = а

Определение арксинуса, арккосинуса, арктангенса. Формулы корней, особую форму записи решений для частных случаев

Решение тригонометрических уравнений, приводимых к квадратному

Основные тригонометрические формулы, формулы для решения

простейших тригонометрических уравнений

Решение тригонометрических уравнений методом группировки и разложения на множители

Способы решения уравнений методом группировки и разложением на множители.

Решение однородных тригонометрических уравнений и уравнений, приводимых к ним

Основные формулы для решения уравнений

Решение тригонометрических уравнений, решаемые с помощью формул сложения, понижения степени и других

Основные формулы для решения уравнений

Решение простейших тригонометрических неравенств

Определение простейших тригонометрических неравенств, различные способы их решения

Основные сведения из теории

Арксинус числа

Определение: Арксинусом числа а℮[-1;1] называется такое число α℮[- ; ], синус которого равен а.

Обозначение: arcsina , - ≤ arcsina ≤

Определение: arcsina = α ↔ sinα = а

Свойства: 1) sin(arcsina)=а

2) arcsin(sinα)=α

3) arcsin(-a)=- arcsina

Таблица значений arcsina

а			( )
arcsina

а	-	- (- )	-	-1
arcsina	-	-	-	-

Арккосинус числа

Определение: Арккосинусом числа а℮[-1;1] называется такое число α℮[0;π], косинус которого равен а.

Обозначение: arccosa , 0≤ arccosa ≤ π

Определение: arccosa = α ↔ cosα = а

Свойства: 1) cos(arccosa)=а

2) arccos(cosα)=α

3) arccos(-a)=π- arccosa

Таблица значений arccosa

а			( )
arccosa

а	-	- (- )	-	-1
arccosa				π

Арктангенс числа

Определение: Арктангенсом числа а℮[- ; ] называется такое число α, тангенс которого равен а.

Обозначение: arctga , - ≤ arccosa ≤

Определение: arctga = α ↔ tgα = а

Свойства: 1) tg(arctga)=а

2) arctg(tgα)=α

3) arctg(-a)=- arctga

Таблица значений arctga

а
arctga

а	-	-1	-
arctga

5.4. Уравнение sinx=a

sinx=a

x=(-1)ⁿarcsina+ πn,n Z

5.5. Уравнение cosx=a

cosx=a

x=±arccosa+ 2πn,n Z

5.6. Уравнение tgx=a

tgx=a

x=arctgx+ πn,n Z

2. Примеры и упражнения

Пример: Найти значение выражения:

1) аrcsin1-arcsin(-1)+ arcsin( )+arcsin(- ) =

= -(- )+ +(- )= + + - = ⁽³+ ⁽³+ ⁽¹- ⁽²= =

2) tg(2 arcsin )=tg(2∙ )=tg =

3) cos(аrcsin(tg ))= cos(аrcsin1)= cos =0

4) аrcsin(cos(аrcsin( tg( )))=аrcsin(cos(аrcsin( ∙1))= =аrcsin(cos(аrcsin ))= аrcsin(cos )= аrcsin =

5) 2аrccos0+3arccos1=2∙ +3∙0= +0=π

6) 12аrccos -3arccos(- )=12∙ -3∙ =2π-2π=0

7) аrccos (- )+3аrcsin(-1)= +3∙(- )=

-

8) sin(6аrccos )= sin(6∙ )= sinπ=0

Пример 2: Решить тригонометрическое уравнение:

(1-2sinх)(1-3cosх)=0

Решение:

1-2sinх=0 или 1-3cosх=0

-2sinх=-1 - 3cosх=-1

sinх= cos=-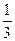

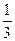х₁=(-1)ⁿarcsin +πn,n℮Z х₂=±arccos(- )+πn,n℮Z

х₁=(-1)ⁿ∙ 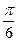+πn,n℮Z х₂=-arccos 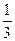+πn,n℮Z

Ответ: х₁=(-1)ⁿ∙ 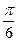+πn,n℮Z х₂=-arccos 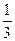+πn,n℮Z

Пример 3: Решить тригонометрическое уравнение:

.

Решение:

.

.

Разделим левую и правую части уравнения на : .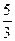

Ответ:

Пример 4: Решить тригонометрическое уравнение:

2sin²х+sinх-6=0

Решение:

Пусть sinх=t, t℮[-1;1]

2t²+t – 6 = 0

Решение:

а=2, b=1, с=-6

t_{1,2= =}

t₁= t₂=

t₁ = [-1;1],т.е. не уд. t₂ = -2 [-1;1],т.е. не уд.

Ответ: решений нет

Пример 5: Решить тригонометрическое уравнение:

2sin²х+5cosх-5=0

Решение:

2(1-cos²х)+5cosх-5=0

2-2cos²х+5cosх-5=0

-2cos²х+5cosх-3=0 :(-1)

2cos²х-5cosх+3=0

Пусть cosх=t, t℮[-1;1]

2t²-5t +3 = 0

а=2, b=-5, с=3

t_{1,2= =}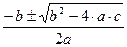

t₁= t₂=

t₁= t₂=1

cosх= [-1;1],т.е. не уд. cosх=1(частный случай)

х=2πn,n℮Z

Ответ: х=2πn,n℮Z

Пример 6: Решить тригонометрическое уравнение:

4sin²x-5sinx∙cosx-6cos²x=0

Решение:

4sin²x-5sinx∙cosx-6cos²x=0(разделим на то, что стоит перед знаком «=», т.е. на cos²х)

=0

4tg²x-5tgx-6=0

Пусть tgx=t

4t²-5t-6=0

а=4, b=-5, с=-6

t_{1,2= =}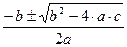

t₁= t₂=

t₁=2 t₂=-

tgx=2 tgх=-

х₁= arctg2+πn,n℮Z х₂= arctg(- )+πn,n℮ Z,

Ответ: х₁= arctg2+πn,n℮Z, х₂=-arctg +πn,n℮Z

Варианты контрольной работы

Задание 1: Найти значение выражения

Вариант 1:

Вариант 2:

Вариант 3:

arcsin +4 arcsin - arccos + аrctg

Вариант 4:

arcsin(сos(аrctg ))

Вариант 5:

аrctg +аrccos

Вариант 6:

Вариант 7:

Вариант 8:

Вариант 9:

аrctg (сos(аrctg 1))

Вариант 10:

аrctg -12аrcsin(- )

Вариант 11:

аrcsin(- 1) + аrccos (-1) +аrctg 0

Вариант 12:

cos(аrctg )

Вариант 13:

arctg1+ arccos - arcsin - аrctg

Вариант14:

аrctg(- )+ аrccos(- )-аrcsin(- )

Вариант 15:

arcsin +4 arcsin - arccos + аrctg

Вариант 16:

аrccos(- )+ аrctg 1

Вариант 17:

аrcsin1 + аrccos 1 +аrctg 0

Вариант 18:

аrcsin0 + аrccos +аrctg 0

Вариант19:

аrctg 1+аrcsin

Вариант 20 :

аrccos + аrctg 1

Вариант 21:

аrccos(- )- аrctg(- 1)

Вариант 22:

аrctg (-1)-аrcsin(- )

Вариант 23:

cos(аrctg )

Вариант 24:

tg(аrcsin )

Вариант 25:

tg(аrcsin )

Вариант 26:

cos(аrctg )

Вариант 27:

аrctg(- )- аrcsin(- )+ аrccos (- )

Вариант 28:

arcsin +4 arcsin - arccos + аrctg

Вариант 29:

аrctg(- )+ аrccos(- )-аrcsin(- )

Вариант 30:

arctg1+ arccos - arcsin - аrctg

Задание 2: Решить тригонометрическое уравнение:

Вариант 1:

1) sinx=

2) 3cos²x – 5cosx +2 =0

3)

Вариант 2:

1) sinx=

2) 4sin²x -11sinx +8 =0

3)

Вариант 3:

1) (2sinx+1)(2sinx-