Решение логарифмических уравнений

Теорема: Пусть а>0, а≠1. Пусть дана функция у =f(х) и действительное число b. Тогда уравнение log_а f(х)=b и уравнение f(х)=а^b равносильны.

Решение логарифмических неравенств

Теорема: Пусть а>0, а≠1,х₁>0, х₂>0 Если log_аf(х)>b, то

1) при а>1 f(х)>a^b (знак сохраняем)

2) при 0<a<1 f(х)<a^b (знак меняем)

Алгоритм решения логарифмического неравенства log_аf(х)>b:

• Найти О.О.Ф. (область определения функции)

О.О.Ф.: под логарифмическое выражение строго больше нуля (f(х)>0);

• По основанию логарифма определить сохранность знака;
• Решить непосредственно само логарифмическое неравенство;
• Составить систему из двух неравенств (П.1+П.3)
• Решить данную систему, совместив оба решения на числовой оси.

2. Примеры и упражнения

Пример 1: Вычислить

1) log₂32=5, т.к. 2⁵=32

2) log₂ =-5, т.к. 2^-5=

3) log₆18+ log₆2= log₆(18·2)= log₆36=2

4) log₁₂48- log₁₂4= log₁₂12= 1

Пример 2:Решить логарифмическое уравнение:

log₆(3х+15)=2

Решение:

3х+15=6²

3х+15=36

3х=36-15

3х=21

х=

х=7 Ответ:х=7

Пример 3:Решить логарифмическое уравнение:

log₃(х²-6х+17)=2

Решение:

х²-6х+17=3²

х²-6х+17=9

х²-6х+17-9=0

х²-6х+8=0

а=1, b=-6, с=8

х_{1,2= ==}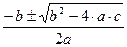

х₁= х₂=

Ответ: х₁=4, х₂=2

Пример 4: Решить логарифмическое уравнение:

(log₂х)²+8 log₂х-9=0

решение:

Пусть log₂х =t

t² +8· t –9 =0

а=1, b=8, с=-9

t_{1,2= =}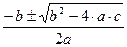

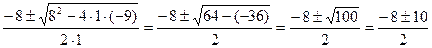
t₁= 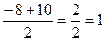t₂=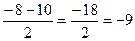

t₁=1 t₂=-9

log₂х =1 log₂х =-9

х₁=2¹ х₂=2^-9

х₁=2 х₂=

х₂=

Ответ: х₁=2, х₁=

Пример 5: Решить логарифмическое уравнение:

log₂(х-5) +log₂(х+2)=3

Решение:

log₂(х-5)·(х+2)=3

(х-5)·(х+2)=2³

х²+2х-5х-10=8

х²+2х-5х-10-8=0

х²-3х-18=0

а=1, b=-3, с=-18

х_{1,2= =}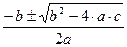

х₁= х₂=

Примечание: В уравнениях данного вида необходимо выполнить проверку.

Проверка:

1) х₁=6

log₂(6-5) +log₂(6+2)= log₂1 +log₂8=0=3=3

3=3

2) х₂=-3-неуд

log₂(-3-5) +log₂(-3+2)= log₂(-8) +log₂(-1) ( формула log_ах₁+ log_ах₂= log_а(х₁·х₂)

справедлива при а>0, а≠1, х>0, х₁>0, х₂>0)

корень х₂=-3 является посторонним.

Ответ: х=6

Пример 6: Решить логарифмическое неравенство:

log₂(3х-4)>5

Решение:

1) О.О.Ф.: 3х-4>0 2) т.к.2>1, то знак сохраняем 3) х>

3х>0+4 3х-4>2⁵ х>12

3х>4 3х-4>32

х> 3х>32+4

х> 3х>36

х>

х>12

Ответ: х>12

Варианты контрольной работы

Задание 1: Вычислить

Вариант 1: log₃12+log₃4,5-log₃6

Вариант 2: Log₅24-log₅120-log₅5

Вариант 3: 7^log₇²¹

Вариант 4: 4^log₂³

Вариант 5:Log₂216·log₅25-3log₂4

Вариант 6: 3^log₃² ·log₅5+3log₄16

Вариант 7: log₃12+log₃4,5-log₃6

Вариант 8: Log_1/525·log₁₆64

Вариант 9: Log₆2+log₆3+2^log₂⁴

Вариант 10: Log₂12-log₂3+3^log₃⁸

Вариант 11: Log₇7-log₇24+log₇24

Вариант 12: Log₃9+log₂1/8: 7^log₇⁴

Вариант 13: Log₃9·log₄1/2+log₆6

Вариант14: 25^log₅³

Вариант 15:15^log₁₅⁹ : 10^log₁₀⁴

Вариант 16: Log₃81·log₁₆64

Вариант 17: Log₇7-log₇24+log₇24

Вариант 18: Log₅25-log₁₆64

Вариант1 9: Log₃9·log₄16+log₅5

Вариант 20: Log_1/33+log_1/33-log_1/33

Вариант 21: Log₅25+log₅3-log₅3

Вариант 22: 15^log₁₅⁹ : 10^log₁₀⁴

Вариант 23: Log_1/51/25·log₁₆64

Вариант 24: Log₃81·log₂₇9

Вариант 25:Log₆2+log₆3

Вариант 26: Log₂12-log₂3

Вариант 27: Log₇8-log₇56

Вариант 28: Log_1/39+log₂1/8: 7^log₇²

Вариант 29: Log₂1/16+log₂8: 9^log₃⁵

Вариант 30: Log₃₆36+log₆3+log₆2

Задание 2: Решить логарифмическое уравнение

Вариант 1:

Log10(2-x)=log10(x-6)

Log3x+log3(x+2)=1

Вариант 2:

Log3(4x-3)=2

(log3x)2-6log3x+9=0

Вариант 3:

Log5(2x+7)=log5(x-3)

Log7(5-x)+log72=1

Вариант 4:

Log1/2(3x-1)=-3

Log7(x2-2x-8)=0

Вариант 5:

Log3(4x-3)=2

Log1/2(x2+4x-5)=-4

Вариант 6:

Log2(3x-4)=3

Log1/2(x2-5x+6)=-1

Вариант 7:

Log2(2x-1)=3

Log2(x2-4x+4)=4

Вариант 8:

Log3(2x+1)=log339

Log3(x-2)+log3(x+6)=2

Вариант 9:

Log1/2(3x-1)=-3	Log4(13+x)+log4(4-x)=2
Вариант 10: Log2(7x-4)=log252	(log2x)2-9log2x+10=0

Вариант 11:

Log4(5x+6)=3

Log7(5-x)+log72=1

Вариант 12:

Log3(12-5x)=2

Log10(2-x)+log102=log1016

Вариант 13:

Log2(x+3)=log2(2x-4)

(х2-4х+12)=-2

Вариант14:

Log10(5x+2)=log1012

log9(х2+2х +6)=1

Вариант 15:

Log2(2x+1)=log212

(log4х)2-2log4х-8=0

Вариант 16:

Log2(3x-4)=3

(log3х)2-4log3х+3=0

Вариант 17:

log6(2х+5)=2

(log3х)2-log3х-2=0

Вариант 18:

log4(8+3х)=3

2(log2х)2-5log2х-6=0

Вариант1 9:

(6х-7)=-3

log2(х-2) +log2(х-3)=1

Вариант 20:

(2х-9)=-7

( log3х)2 +5log3х-6=0

Вариант 21:

log4(2х-8)=3

(log7х)2 -5log7х+6=0

Вариант 22:

log13(7х-1)=1

(log4х)2 +log4х-6=0

Вариант 23:

log2(3х+4)=4

(log3х)2 +log3х-2=0

Вариант 24:

log17(5х-3)=1

(х2 –4х-2)=-1

Вариант 25:

Log3(12-5x)=2

log3(х2 –х+7)=2

Вариант 26:

(2х-9)=-7

log4(х2 -3х+18)=2

Вариант 27:

Log3(4x-3)=2

(х2-2х+46)=-2

Вариант 28:

Log2(2x+1)=log212

(log4х)2-2log4х-8=0

Вариант 29:

Log2(3x-4)=3

Log1/2(x2-5x+6)=-1

Вариант 30:

Log2(2x-1)=3

Log2(x2-4x+4)=4

Задание 3: Решить логарифмическое неравенство

Вариант 1: Log₇(2x-1)< 2

Вариант 2: Log₁₀0,5x<-2

Вариант 3: Log₂(x-4) >1

Вариант 4: Log_1/3(2x-7) >-2

Вариант 5: Log₄(3-2x)< 2

Вариант 6: Log₂(2x-3)< 3

Вариант 7: Log₂(2x+3) >2

Вариант 8: Log₅(x-1) >1

Вариант 9: Log₃(2x-1)< 3

Вариант 10: Log₁₀x >2

Вариант 11: Log₁₀2x< 1

Вариант 12: Log₅(1-3x)< 2

Вариант 13: Log₂(1-2x) >0

Вариант14: Log_1/3(2x-1) >-2

Вариант 15:Log₁₀(3-2x)< 2

Вариант 16: Log₆(5x-2) >2

Вариант 17: Log_1/2(2x+1) >-2

Вариант 18: Log₃(5x-6)< 2

Вариант1 9: Log₇(x-1)< 2

Вариант 20: Log_1/2(2-x) >-1

Вариант 21: 2 Log₄(7-x)< 3

Вариант 22: Log₃(4-3x) >1

Вариант 23: Log₂(1-2x)< 0

Вариант 24: Log₂(2x+1) >4

Вариант 25:Log₅(3x+1)< 2

Вариант 26: Log₅(4x+1) >-1

Вариант 27: Log_1/5(2x+3) >-3

Вариант 28: Log_1/22x >2

Вариант 29: Log₃(5x+4) >3

Вариант 30: Log₁₀(2x+1)< 0

Содержание темы «Степенная функция»

Определение и свойства степенной функции.

Свойства и графики различных случаев степенной функции. Сравнение чисел, решение неравенств с помощью графиков и (или) свойств степенной функции.

Иррациональные уравнения.

Определение равносильных уравнений, следствия уравнения; при каких преобразованиях исходное уравнение заменяется на равносильное ему уравнение, при каких получаются посторонние корни, при каких происходит потеря корней; Определение иррационального уравнения;

Иррациональные неравенства.

Определение иррационального неравенства; алгоритм решения этого неравенства

Решение систем двух уравнений с двумя неизвестными.

Алгоритмы решения систем двух уравнений с двумя неизвестными.

Основные сведения из теории

3.1. Определение и свойства степенной функции

Определение: Функцию у=х^р, где р - заданное действительное число, называют степенной функцией.

Свойство 1: Степенная функция у=х^р для любого р R определена при х>0

Свойство 2: Множество значений степенной функции у=х^р при х>0, р≠0 – все положительные числа

Свойство 3: Степенная функция у=х^р на интервале х>0 является возрастающей, если р>0, и убывающей, если р<0.