Подбор аппроксимирующей функции по методу трех выбранных точек.

№	Вид формулы		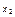		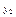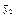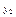-	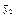Примечание
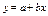			1,370	1,3624	0,0076	Не подходит
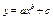			1,363	1,3622	0,0008	Мало подходит
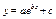			1,370	1,3622	0,0078	Не подходит
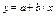			1,3624	1,3624	0,0000	Подходит
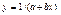			1,370	1,3624	0,0076	Не подходит
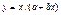			1,3621	1,3624	0,0003	Мало подходит
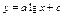			1,3633	1,3624	0,0007	Мало подходит

Из анализа расчетов, представленных в таблице 11 делаем заключение, что наилучшим образом для аппроксимации опытных данных подходит гиперболическая функция 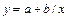, параметры которой определяются вышеизложенными методами.

Вопросы для контроля

1. Что является аналитическим признаком существования линейной аппроксимирующей зависимости для опытных данных?

2. Что является признаком существования линейной зависимости для описания опытных данных с равноотстоящими точками?

3. При каком условии опытные данные можно описать квадратичной зависимостью?

4. При каком условии опытные данные для равноотстоящих точек будут описываться полиномом 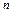- й степени?

5. В чем суть метода трех выбранных точек?

6. По какому выражению находятся ординаты 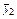для линейной функции по методу трех точек?

7. По какому выражению находится абсцисса второй точки гиперболической (и других) функции?

8. Изложите последовательность алгоритма для проверки пригодности функции для аппроксимации опытных данных?

7. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЭМПИРИЧЕСКОЙ ФУНКЦИИ

После выбора вида эмпирической функции решается задача по определению наилучших параметров (коэффициентов), входящих в выбранную формулу. Для нахождения коэффициентов функции используются три метода: метод выбранных точек, метод средних и метод наименьших квадратов. Иногда полезно применять их комбинацию. Для замены сложных аналитических функций более простыми аппроксимирующими выражениями используется интегральный метод наименьших квадратов.

7.1. Метод выбранных точек

Вычисления по методу выбранных точек проводятся в следующей последовательности.

1. На кривой сглаженного графика выбирают такое количество 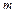точек, которое равно числу неизвестных коэффициентов формулы.

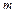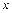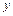2. Каждую из пар опытных значений и подставляют в аппроксимирующее уравнение, что дает систему 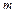уравнений с 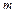неизвестными.

3. Полученную систему уравнений решают относительно неизвестных коэффициентов формулы.

Применение этого метода для линейного уравнения 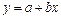рассмотрен в разделе «Линейная функция», см. (13)…(17).

Для квадратичной зависимости

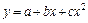(76)

коэффициенты 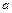, , 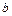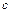определяются из системы трех уравнений

;

;

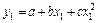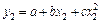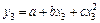. (77)

Точки с координатам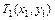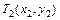и , и 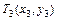берутся на кривой сглаженного графика. Для удобства проведения расчетов желательно, чтобы абсциссы 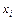этих точек совпадали с обозначенными делениями оси .

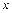Метод выбранных точек содержит геометрические построения (графическое сглаживание, отсчет ординат), допускающие погрешности как при построении сглаживающей кривой, так и при отсчете ординаты 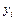, поэтому точность его невелика

7.2. Метод средних

Метод средних базируются на следующем положении. По экспериментальным точкам можно построить несколько кривых. Наилучшей будет та, у которой отклонения 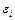от экспериментальных значений будут наименьшие, т.е. .

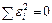Метод средних предполагает следующий порядок вычисления коэффициентов аппроксимирующего уравнения.

1. В подобранное для аппроксимации выражение 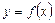подставляют значения координат 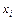и 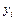всех экспериментальных точек, получая систему из 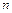уравнений. Каждое уравнение приравнивают соответствующему отклонению 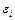. Например, система начальных уравнений, когда в качестве аппроксимирующей функции выбран полином 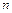- ой степени

,

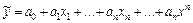имеет вид

;

;

… … …

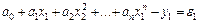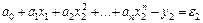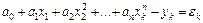. (78)

2. Как правило, количество экспериментальных точек, а следовательно и число уравнений системы (78), больше числа неизвестных коэффициентов 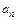. Эти коэффициенты вычисляются с использованием следующего приема. Система начальных уравнений разбивается на 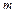групп, количество которых должно быть равно числу определяемых коэффициентов .

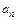3. Уравнения в каждой группе почленно складываются, получая новую систему, число уравнений в которой равно количеству групп.

4. Решая полученную систему уравнений определяют коэффициенты аппроксимирующей функции , ,…, .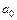

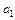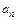Точность метода повышается, если провести вычисления для 2 – 3 вариантов группировки начальных уравнений (78) и выбрать аппроксимирующую функцию с теми коэффициентами, для которой 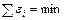. Желательно, чтобы число уравнений в каждой начальной группе, по возможности, было одинаковым.

П р и м е р 10. При испытании двигателя внутреннего сгорания на режимах скоростной характеристики получена следующая зависимость крутящего момента 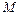от частоты вращения коленчатого вала 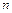(таблица 12). Подобрать эмпирическую формулу для зависимости .

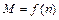Таблица 12