Опытные и расчетные данные подбора параметров степенной функции

Опытные данные
	1,15	1,50	1,80	2,00	2,00	2,35
Расчетные данные		1,609	2,302	2,708	2,996	3,219	3,401
	0,140	0,405	0,588	0,693	0,788	0,854
	1,150	1,515	1,780	1,996	2,182	2,350
		-0,015	0,020	0,004	0,018

Р е ш е н и е. Опытные данные не группируются по прямой линии, поэтому представим их в логарифмической системе координат и . По данным , , сведенным в табл. 2. строится график функции (рис. 6).

Рис. 6. График функции .

Как видно из рис. 6, опытные точки группируются около прямой линии. Поэтому функция является линейной.

Для определения коэффициентов 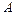и 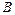уравнения используется любой метод: графический, метод двух точек, метод парных точек.

Определим коэффициенты 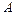и 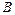по методу двух точек (первой и шестой) по формулам (17).

;

.

Переход от коэффициентов линейной функции

, (26)

к степенной аппроксимирующей функции проведем по (25)

= e^0,501 = 0,608, = 0,398.

Эмпирическая формула, описывающая опытные данные примера 3 имеет вид

. (27)

Значения , вычисленные по (27) и их отклонения от опытных данных представлены в таблице 2.

.

В общем случае степенная функция представляется в виде

, (28)

для линеализации используется уравнение

, (29)

прологарифмировав которое получим

. (30)

Сведем (30) к линейному уравнению , заменив

; , , . (31)

Первоначально вычисляется параметр 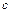одним из численных методов математического анализа

, (36)

Когда параметр 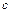определен, решаем уравнение как обычно

,

. (37)

Заменив , , , , получим линейное уравнение вида

, (38)

параметры 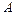и 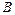которого определяются любым известным методом. Переход от параметров 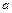и степенной функции производим по (25).

Показательная функция имеет вид

. (39)

Первоначально определяется параметр по (36)

Далее уравнение (39) прологарифмируем в виде

. (44)

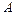Заменив , , , получим линейное уравнение вида в полулогарифмической системе координат , (рис. 7), параметры которого определяются любым известным методом. Переход от параметров и 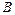линейной функции к параметрам 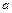и показательной функции осуществляется следующим образом , отсюда -

, . (45)

Логарифмическая функция вида

приводится к линейной заменой

ln x = X, c = A, a = B.

Гиперболическая функция вида

(46)

приводится к линейной заменой

, , , . (47)

Гиперболическая функция переходит в прямую в прямоугольной системе координат при и .

Дробно-линейная функция

, (48)

сводится к линейной заменой переменной , тогда (48) записывается в виде

или . (49)

График функции - прямая в прямоугольной системе координат, где , , , .

Дробно-рациональная функция вида

приводится к линейной следующим преобразованием:

и далее .

Дробно-рациональная функция переходит в прямую в прямоугольной системе координат при , , , .

П р и м е р 4. По результатам эксперимента, приведенным в таблице 4, подобрать эмпирическую функцию.

Таблица 4

Опытные и расчетные данные подбора параметров функции примера 4

Опыт			0,2	0,4	0,6	0,8	1,0	1,2	1,4
		2,4	1,7	1,4	1,1	0,95	0,8	0,7
Расчет		0,25	0,42	0,59	0,77	0,91	1,05	1,25	1,43
	1,386	0,875	0,530	0,262	0,095	-0,051	-0,223	-0,357

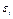Нанесем точки на прямоугольную систему координат (рис. 8). Как видно из рис. 8, опытные точки ближе всего располагаются по кривой соответствующей дробно-линейной функции (рис. 2) вида

, (50)

и показательной функции (рис. 2)

. (51)

Опытные данные, соответствующие дробно-линейной функции (50), должны укладываться на прямую линию в прямоугольной системе координат , где . Для показательной функции (51) опытные значения должны располагаться по прямой линии в полулогарифмической системе координат , где .

Для проверки выдвинутых предположений о виде аппроксимирующей функции нанесем опытные значения (табл. 4) в координатах и (рис. 9).

Рис. 8. Расположение опытных точек.

Анализируя данные по рис. 9, видим, что опытные значения лучше выравниваются для функции и описываются уравнением

, (52)

параметры которого можно определить графически по рис. 9.

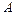= 0,25; 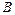= (1,43 – 0,25)/1,4 = 0,84.

Искомая эмпирическая функция принимает вид (50), в которой , :

. (53)

Одни и те же экспериментальные данные с достаточной точностью могут быть описаны различными эмпирическими формулами, но предпочтение следует отдавать той, которая ближе соответствует физической сущности описываемого явления, наиболее проста и употребительна в данной области исследований.

Рис. 9. Графическая проверка опытных данных на линейность.

● - ; ▲- .

Вопросы для контроля

1. В чем заключается суть метода линеализации аппроксимирующих функций?

2. В каких координатах степенная функция изображается в виде прямой линии?

3. Из какого условия определяется параметр степенной функции ?

4. В каких координатах показательная функция изображается в виде прямой линии?

5. Из какого условия определяется параметр показательной функции ?

6. В каких координатах гиперболическая функция приводится к линейной?

7. Какие преобразования необходимо произвести для того, чтобы дробно-линейную функцию свести к линейной зависимости?

5. ВЫБОРА ВИДА ЭМПИРИЧЕСКОЙ ФОРМУЛЫ

ПО МЕТОДУ ТРЕХ ВЫБРАННЫХ ТОЧЕК

Суть метода сводится к следующему. Из заданной системы точек выбирается три точки: 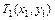- в начальной области 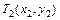– в промежуточной и 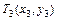– в конечной. Полагая, что аппроксимирующая линия проходит через эти точки, промежуточная точка 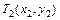выбирается таким образом, чтобы аппроксимирующее уравнение было, по возможности, простым. Чтобы точка 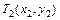находилась на аппроксимирующей линии подбирается значение по заданным значениям и .

Наиболее приемлемыми значениями являются:

среднее арифметическое значений и

; (65)

среднее геометрическое значений и

(66)

и среднее гармоническое значений и

. (67)

Для линейной аппроксимирующей функции возьмем в виде среднего арифметического от и , т.е.

, (68)

тогда значения функции в трех выбранных точках записывается в виде

;

;

(69)

или

;

. (70)

Из (68) и (70) следует, что для существования линейной зависимости необходимым условием является, чтобы среднему арифметическому значений и соответствовало среднее арифметическое значений и .

Для получения необходимого условия существования степенной зависимости полагаем средним геометрическим значений и

. (71)

Значения функции в трех выбранных точках будут равны

,

,

. (72)

Учитывая, что

, (73)

второе уравнение (72) будет иметь вид

. (74)

Из (71) и (74) следует, что для существования степенной зависимости необходимым условием является, чтобы среднему геометрическому значений и соответствовало среднее геометрическое значений и .

Если степенная функция имеет вид , то определяется по формуле (74) с вычитанием из и параметра 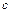, которое определяется по (36) ,

. (75)

Аналогичным образом выводится необходимые условия существования для других функций.

В таблице 9 приведены необходимые условия существования для наиболее употребляемых функций, использующихся для аппроксимации опытных данных.

Таблица 9.