Раздел. Комплексные числа. Алгебра многочленов.
47. Комплексное число, его изображение на плоскости. Комплексно-сопряжённое число. Модуль и аргумент комплексного числа. Различные формы записи комплексного числа (алгебраическая, тригонометрическая, показательная). Формула Эйлера.
48. Действия над комплексными числами (сложение, вычитание, умножение, деление) в алгебраической, тригонометрической и показательной формах.
49. Возведение комплексного числа в степень. Формула Муавра. Извлечение корня из комплексного числа.
50. Понятие многочлена, алгебраического уравнения. Основная теорема алгебры и теорема Безу. Разложение многочлена на множители. Нахождение корней квадратного уравнения.
Приложения.
6.1. Образец решения контрольных задач типового варианта.
1 – 10.Вычислить определитель: 
а)непосредственным разложением по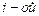 
строке;
б)непосредственным разложением по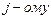 
столбцу;
Решение. а)вычисляем определитель разложением по элементам первой строки: 
= 
.
Тогда 
= 
= 
б)вычисляем определитель непосредственным разложением по элементам
второго столбца: 
= 
.
Тогда = = 
.
Ответ: 
.
11-20.Найти матрицу
,если:
, 
.
Решение:
1)Транспонируем матрицу
: 
.
2)Вычисляем произведение матриц 
:
.
3)Находим матрицу 
:
.
4)Находим матрицу 
: 
.
Ответ: 
.
21 – 30. Дана система уравнений: 
. Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а)Вычисляем определитель системы и проверяем, что он отличен от нуля:
.
2а) Так как 
, то система имеет единственное решение, определяемое формулами Крамера: 
3а) Вычисляем определители 
:
,
,
.
4а) Находим решение: 
.
5а) Выполняем проверку: 
.
Ответ: 
.
Б) Метод обратной матрицы.
1б)Записываем систему уравнений в матричном виде:
или 
2б)Вычисляем определитель системы и проверяем, что он отличен от нуля:
3б) Так как 
, то матрица системы имеет обратную матрицу 
и единственное решение системы определяется формулой:
или 
4б)Находим обратную матрицу 
(методом присоединённой матрицы):
.
Тогда 
.
5б)Находим решение:
.
6б) Выполняем проверку: 
.
Ответ: 
.
В) Метод Гаусса.
1в)Записываем расширенную матрицу системы:
.
2в)Выполняем прямой ход метода Гаусса.
В результате прямого хода матрица системы 
должна быть преобразована с помощью элементарных преобразований строк к матрице 
треугольного или трапециевидного вида с элементами 
. Система уравнений, матрица которой является треугольной с элементами 
, имеет единственное решение, а система уравнений, матрица которой является трапециевидной с элементами 
, имеет бесконечно много решений.
.В результате элементарных преобразований матрица системы преобразована к специальному виду 
. Система уравнений, матрица которой , является треугольной с ненулевыми диагональными элементами , имеет всегда единственное решение, которое находим, выполняя обратный ход.
Если при выполнение преобразования расширенной матрицы 
в преобразованной матрице 
появляется строка 
, где 
, то это говорит о несовместности исходной системы уравнений.
3в)Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 
и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных: 
.
4в) Выполняем проверку: .
Ответ: .
31-40.Найти общее решение для каждой из данных систем методом Гаусса:
а) 
.
Решение.
1а)Записываем расширенную матрицу системы:
.
2а)Выполняем прямой ход метода Гаусса.
.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных 
и 
: 
. Поэтому выбираем в качестве базисных – неизвестные и , тогда свободными будут неизвестные 
и 
.
3а)Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 
. Свободным неизвестным придаём разные, произвольные постоянные значения: 
, 
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: 
.
Тогда общее решение системы запишется в виде: 
.
4а) Выполняем проверку:
.
Ответ: .
б) 
.
Решение.
1а)Записываем расширенную матрицу системы:
.
2а)Выполняем прямой ход метода Гаусса.
В результате прямого хода матрица системы должна быть преобразована с помощью элементарных преобразований строк к матрице треугольного или трапециевидного вида с элементами .
Если, при выполнении преобразования расширенной матрицы , в преобразованной матрице появляется строка , где , то это говорит о несовместности исходной системы уравнений.
Для выполнения условия может потребоваться перестановка местами столбцов матрицы системы. Если при выполнении преобразований прямого хода в матрице системы переставлялись местами столбцы коэффициентов при неизвестных, то в дальнейшем, при записи системы уравнений, соответствующей последней расширенной матрице прямого хода, это следует учесть.
.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных и : 
. Поэтому выбираем в качестве базисных – неизвестные и , тогда свободными будут неизвестные и .
3б)Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 
. Свободным неизвестным придаём разные, произвольные постоянные значения: 
, , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: 
.
Тогда общее решение системы запишется в виде:
4б) Выполняем проверку:
Ответ: .
в) 
.
Решение.
1в)Записываем расширенную матрицу системы:
.
2в)Выполняем прямой ход метода Гаусса.
.
При выполнении преобразования расширенной матрицы , в преобразованной матрице появилась строка 
, соответствующая уравнению 
, которому не удовлетворяет ни один набор значений неизвестных 
, что говорит о несовместности исходной системы уравнений.
Ответ: Система несовместна.
41 – 50.Требуется:
а)найтисобственные числа и векторы матрицы .
Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы : 
, а множество собственных векторов, отвечающих собственному числу 
, совпадает с множеством ненулевых решений матричного уравнения: 
, определяемым методом Гаусса.
Решение:
1) Составляем характеристическое уравнение матрицы :
.
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):
, 
.
Таким образом, собственными числами матрицы являются: 
и .
2)Находим собственные векторы матрицы , отвечающие различным собственным числам 
и 
.
2.1)Составляем матричное уравнениедля нахождения собственных векторов 
, отвечающих собственному числу : 
или
,
записываем его в виде системы линейных уравнений: 
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 
, имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной : 
. Поэтому выбираем в качестве базисной – неизвестную , тогда свободными будут неизвестные и . Свободным неизвестным придаём разные, произвольные постоянные значения: 
, 
, где 
, 
, одновременно, и выражаем через них значение базисной неизвестной из уравнения системы: 
. Тогда общее решение системы, задающее множество всех собственных векторов , отвечающих собственному числу будет иметь вид: 
.
2.2)Составляем матричное уравнениедля нахождения собственных векторов 
, отвечающих собственному числу : 
или
,
записываем его в виде системы линейных уравнений: 
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 
, имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных и : 
. Поэтому выбираем в качестве базисных – неизвестные и , тогда свободной будет неизвестная . Свободной неизвестной придаём произвольное постоянное значение: 
, где 
и выражаем через неё значения базисных неизвестных и из уравнений системы специального (трапециевидного) вида, начиная с последнего уравнения: 
. Тогда общее решение системы, задающее множество всех собственных векторов 
, отвечающих собственному числу , будет иметь вид: 
, .
Ответ: , , , ;
, , .
б)исследовать квадратичную форму 
на знакоопределённость (по критерию Сильвестра).
Решение.
1)Записываем матрицу квадратичной формы: 
.
2) Проверяем является ли матрица невырожденной. Для этого вычисляем её определитель 
и проверяем, равен ли он нулю: 
. Так как 
, то матрица - невырожденная и, следовательно, для исследования квадратичной формы на знакоопределённость можно применить критерий Сильвестра.
3)Вычисляем угловые миноры матрицы и делаем вывод о знакоопределённости квадратичной формы: 
, 
, 
. Так как выполняется условие: 
, 
, 
, то по критерию Сильвестра квадратичная форма положительно определена.
Ответ: Квадратичная форма положительно определена.
51 – 60.Даны векторы 
: 
; 
; 
; 
. Показать, что векторы 
образуют базис 
и найти координаты вектора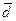 
в этом базисе.
Решение.
1)Покажем, что векторы 
образуют базис .Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
.
Так как 
, то векторы образуют базиси, следовательно, вектор 
единственным образом можно разложить по векторам этого базиса.
2)Записываем разложение вектора 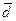по векторам базиса 
:
или 
.
Коэффициенты разложения 
, 
, 
называют координатами вектора 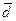в базисе 
и записывают: 
.
3)Записываем векторное уравнение относительно , , в виде эквивалентной ему системы линейных уравнений: 
, и находим
единственное решение системы, например, по формулам Крамера:
, где
, 
, 
, 
.
Таким образом: 
, 
, 
. Следовательно, разложение имеет вид: 
или кратко: 
.
Ответ: 
.
61 – 70.Даны векторы 
: , , . Требуется: а)найти векторы 
и 
; б)вычислить скалярное произведение 
;в)найти проекцию вектора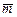 
на направление вектора 
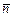; г) найти векторное произведение 
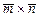и его модуль 
.
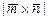Решение.
a)Находимвекторы 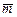и :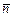
= 
;
= 
.
б)Вычисляем скалярное произведениевекторов :
.
в)Находим проекцию вектора 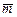на направление вектора :
.
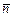г)Находим векторное произведение векторов :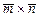
и вычисляем его модуль: =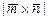 
.
Ответ: а) = ; = ; б) 
;в) 
; г)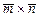 
, 
.
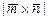
71-80.Даны вершины треугольника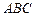 
: 
, 
, 
Требуется найти:
а)длину стороны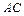
; б)уравнение стороны ;
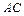в)уравнение медианы 
, проведённой из вершины ;
г)уравнение высоты 
, проведённой из вершины
;
д)длину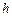 
высоты ; е)площадь 
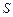треугольника
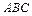.Сделать чертёж.
Решение.Сделаем чертёж:
а)Длинустороны 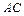находим как длину вектора 
:
,
.
б) Уравнение стороны 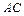находим как уравнение прямой, проходящей через точки 
и 
, и записываем его в виде общего уравнения прямой:
.
в)Уравнение медианы находим как уравнение прямой, проходящей через точки и 
, и записываем его в виде общего уравнения прямой. Неизвестные координаты точки 
находим как координаты точки, делящей сторону 
пополам:
; 
.
Тогда: 
.
г)Уравнение высоты находим как уравнение прямой, проходящей через точку 
перпендикулярно вектору 
, который принимаем за нормальный вектор прямой . Тогда 
д)Длину 
высоты находим как расстояние от точки до прямой 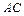, заданной общим уравнением 
:
.
е)Площадь треугольника 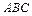находим по формуле: 
. Откуда 
.
Ответ: а)