МАТЕМАТИКА (в четырёх частях): Часть 1.
МАТЕМАТИКА (в четырёх частях): Часть 1.
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
для студентов заочной и дистанционной форм обучения
по инженерно-техническим направлениям подготовки бакалавров
Г. Набережные Челны
Математика (в четырёх частях): Часть 1.Учебно-методический комплекс для студентов заочной и дистанционной форм обучения по инженерно-техническим направлениям подготовки бакалавров. /Составитель: Углов А.Н. -Набережные Челны: Изд-во: НЧИ К(П)ФУ, 2014, 72 с.
1.Цель и задачи дисциплины, её место в учебном процессе.
Цельпреподавания дисциплины «Математика» - формирование системы базовых знаний по данной дисциплине, которая позволит будущим специалистам решать в своей повседневной деятельности актуальные задачи науки и практики, понимать написанные на современном научном уровне результаты других исследований и тем самым совершенствовать свои профессиональные навыки.
Основными задачами дисциплиныявляются:
- ознакомление обучающихся с фундаментальными понятиями и фактами математики, необходимыми для применения современных математических методов при решении задач науки, техники, экономики и управления;
-привлечение внимания студентов к возможностям использования математических методов при исследовании различных задач;
-развитие навыков к математическому моделированию прикладных задач;
-воспитание абстрактного мышления и умения строго обосновать соответствующие факты;
-развитие логического и алгоритмического мышления;
-овладение классическим математическим аппаратом для дальнейшего использования в приложениях.
Данная дисциплина является основой при изучении дисциплин, использующих современные математические методы. В свою очередь, для изучения данной дисциплины необходимо знание элементарной математики.
В результате изучения данной дисциплины студент должен:
- знать теоретические основы линейной и векторной алгебры, аналитической геометрии, дифференциального и интегрального исчислений, дифференциальных уравнений, числовых и функциональных рядов, теории вероятностей и математической статистики;
- уметь использовать полученные знания для решения практических задач.
Изучение дисциплины предусматривает проведение лекционных, практических занятий и самостоятельную работу студентов. В лекциях излагается содержание тем программы с учетом требований, установленных для специалиста в квалификационной характеристике. Практические занятия проводятся с целью закрепления теоретических основ курса, получения практических навыков решения математических задач. Контроль знаний осуществляется с помощью контрольных работ, зачётов и экзаменов.
2. Содержание и структура дисциплины (часть 1).
2.1 Содержание дисциплины (наименование тем).
Раздел. ЛИНЕЙНАЯ АЛГЕБРА.
Тема. Определители.
Определители 2-ого, 3-его, порядков, порядка n. Свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца. Вычисление определителей.
Тема. Матрицы.
Определение матрицы. Виды матриц. Действия над матрицами. Линейная зависимость и независимость строк матрицы. Базисный минор. Ранг матрицы. Обратная матрица, условие существования, основные способы её нахождения. Матричные уравнения, их решение.
Тема. Системы линейных уравнений.
Системы линейных уравнений (СЛУ). Основные понятия и определения. Матричная запись СЛУ. Теорема Кронеккера-Капелли. Формулы Крамера. Решение СЛУ методом обратной матрицы. Решение СЛУ методом Гаусса. Базисные и свободные неизвестные. Общее решение СЛУ. Однородные системы линейных уравнений, свойства их решений. Условия существования ненулевых решений однородных СЛУ. Фундаментальная система решений. Структура общего решения СЛУ.
Тема. Линейные операторы.
Линейный оператор, действия над ними. Собственные векторы и собственные значения линейных операторов, их свойства и нахождение.
Тема. Квадратичные формы.
Квадратичные формы. Закон инерции квадратичных форм. Положительно и отрицательно определённые квадратичные формы. Критерии знакоопределённости квадратичных форм.
Раздел. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Тема. Векторная алгебра.
Геометрические векторы на прямой, плоскости и в пространстве, действия над ними. Проекция вектора. Прямоугольная декартова система координат. Радиус-вектор. Координаты вектора. Линейные операции над векторами в координатной форме. Длина и направляющие косинусы вектора. Расстояние между точками. Деление отрезка в данном отношении. Скалярное, векторное, смешанное произведения векторов, их свойства, выражение в координатной форме, приложения для решения геометрических задач. Условия перпендикулярности, параллельности и компланарности векторов.
Задания для контрольной работы.
1 – 10.Вычислить определитель:
а)непосредственным разложением по 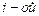 строке;
строке;
б)непосредственным разложением по 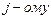 столбцу.
столбцу.
1. 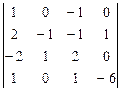 2.
2. 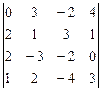 3.
3. 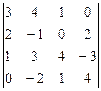
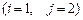
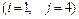
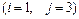
4. 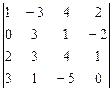 5.
5. 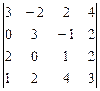 6.
6. 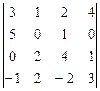
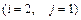
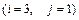
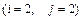
7. 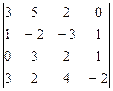 8.
8. 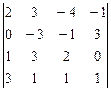 9.
9. 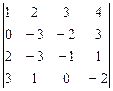
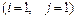
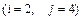
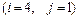
10. 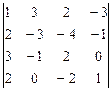
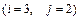
11 – 20.Найтиматрицу 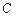 , если
, если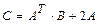 .
.
11. 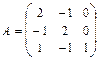 ,
, 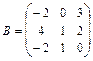 12.
12. 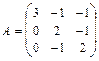 ,
, 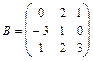
13. 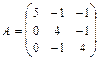 ,
, 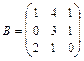 14.
14. 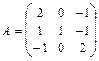 ,
, 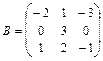
15. 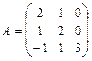 ,
, 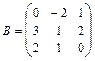 16.
16. 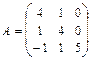 ,
, 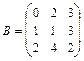
17. 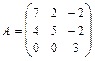 ,
, 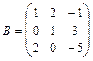 18.
18. 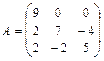 ,
, 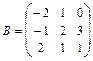
19. 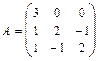 ,
, 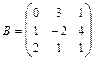 20.
20. 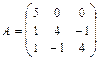 ,
, 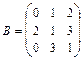 .
.
21 – 30. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера;
б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
21. 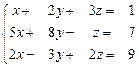 22.
22. 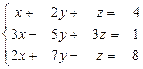
23. 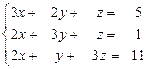 24.
24. 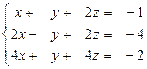
25. 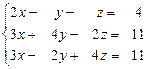 26.
26. 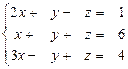
27. 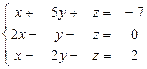 28.
28. 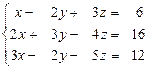
29. 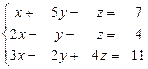 30.
30. 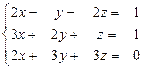
31–40.Найти общее решение системы линейных уравнений методом Гаусса:
31. 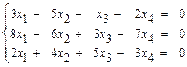 32.
32. 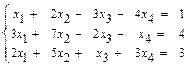
33. 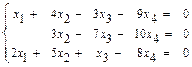 34.
34. 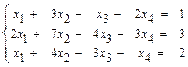
35. 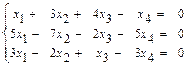 36.
36. 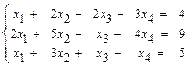 37.
37. 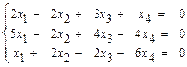 38.
38. 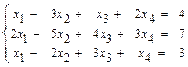
39. 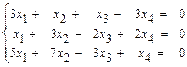 40.
40. 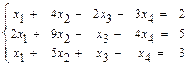
41 – 50.Требуется:
а)найтисобственные числа и векторы матрицы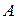 ;
;
б)исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
41. а) 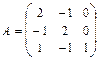 б)
б) 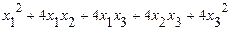
42. а) 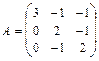 б)
б) 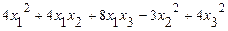
43. а) 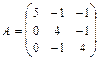 б)
б) 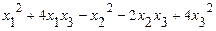
44. а) 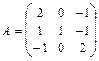 б)
б) 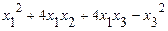
45. а) 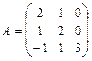 б)
б) 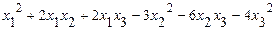
46. а) 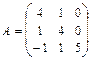 б)
б) 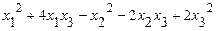
47. а) 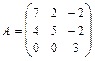 б)
б) 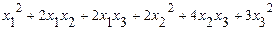
48. а) 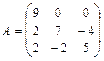 б)
б) 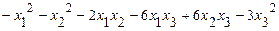
49. а) 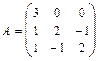 б)
б) 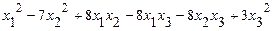
50. а) 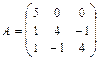 б)
б) 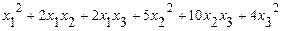
51 – 60.Даны векторы 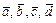 . Показать, что векторы
. Показать, что векторы 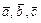 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 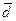 в этом базисе.
в этом базисе.
51. 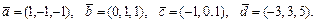
52. 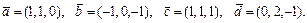
53. 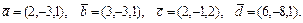
54. 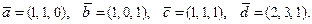
55. 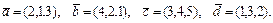
56. 
57. 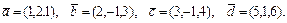
58. 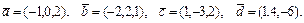
59. 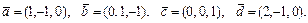
60. 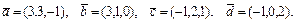
61 – 70.Даны векторы 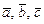 . Требуется:
. Требуется:
а)найти векторы 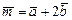 и
и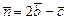 ;
;
б)вычислить скалярное произведение 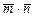 ;
;
в)найти проекцию вектора 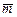 на направление вектора
на направление вектора 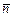 ;
;
г)найтивекторное произведение 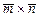 и его модуль
и его модуль 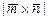 .
.
61. 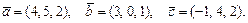
62. 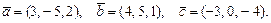
63. 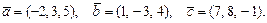
64. 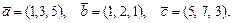
65. 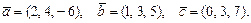
66. 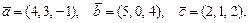
67. 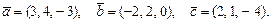
68. 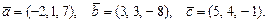
69. 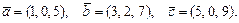
70. 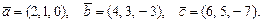
71-80.Даны вершины треугольника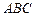 .Требуется найти:
.Требуется найти:
а)длину стороны 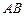 ;б)уравнение стороны
;б)уравнение стороны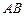 ;
;
в)уравнение медианы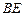 ,проведённой из вершины
,проведённой из вершины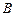 ;
;
г)уравнение высоты 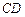 , проведённой из вершины
, проведённой из вершины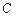 ;
;
д)длину 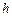 высоты
высоты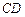 ; е)площадь
; е)площадь 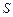 треугольника
треугольника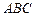 .Сделать чертёж.
.Сделать чертёж.
71. 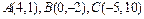 . 72.
. 72. 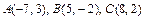
73. 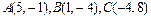 74.
74. 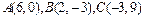
75. 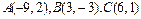 76.
76. 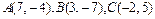
77. 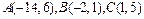 78.
78. 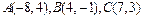
79. 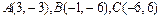 80.
80. 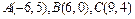
81 – 90.Даны вершины пирамиды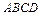 .Требуется найти:
.Требуется найти:
а)длины ребер 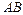 и
и 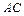 ;б)угол между ребрами
;б)угол между ребрами 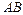 и
и 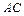 ;
;
в)площадь грани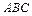 ; г)объем пирамиды
; г)объем пирамиды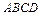 ;
;
д)уравнение плоскости грани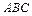 ; е)длину
; е)длину 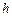 высоты
высоты 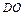 пирамиды.
пирамиды.
81. 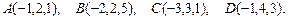
82. 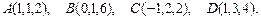
83. 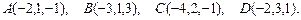
84. 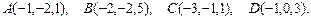
85. 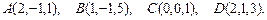
86. 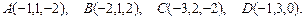
87. 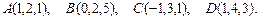
88. 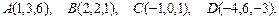
89. 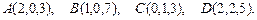
90. 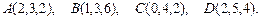
91–100.Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её.
91. 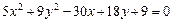 92.
92. 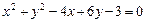
93. 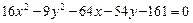 94.
94. 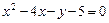
95. 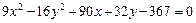 96.
96. 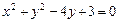
97. 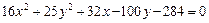 98.
98. 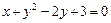
99. 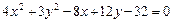 100.
100. 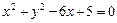
101-110.Даны комплексные числа 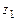 ,
, 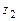 ,
, 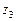 . Требуется: а)вычислить
. Требуется: а)вычислить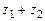 ,
, 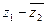 ,
, 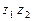 ,
, 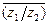 ; б)представить комплексное число
; б)представить комплексное число 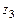 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить 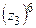 и результат представить в алгебраической форме.
и результат представить в алгебраической форме.
101. 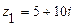 ,
, 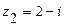 ,
, 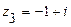 .
.
102. 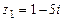 ,
, 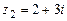 ,
, 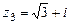 .
.
103. 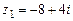 ,
, 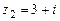 ,
, 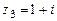 .
.
104. 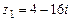 ,
, 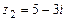 ,
, 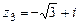 .
.
105. 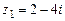 ,
, 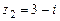 ,
, 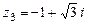 .
.
106. 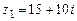 ,
, 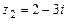 ,
, 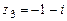 .
.
107. 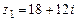 ,
, 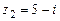 ,
, 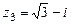 .
.
108. 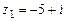 ,
, 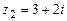 ,
, 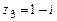 .
.
109. 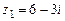 ,
, 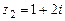 ,
, 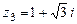 .
.
110. 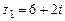 ,
, 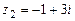 ,
, 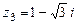 .
.
111-120.Дано алгебраическое уравнение 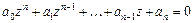 . Требуетсянайти все корни алгебраического уравнения на множестве комплексных чисел.
. Требуетсянайти все корни алгебраического уравнения на множестве комплексных чисел.
111. 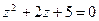 . 112.
. 112. 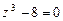 . 113.
. 113. 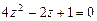 .
.
114. 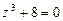 . 115.
. 115. 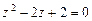 . 116.
. 116. 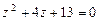 .
.
117. 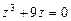 . 118.
. 118. 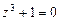 . 119.
. 119. 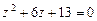 .
.
120. 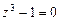 .
.
Вопросы к экзамену (зачёту).
Раздел. Линейная алгебра.
1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.
3. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей.
4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.
5. Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ.
6. Решение, множество решений СЛУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство.
7. Теорема Крамера (о разрешимости СЛУ порядка 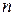 ). Формулы Крамера для решения СЛУ, условия их применимости.
). Формулы Крамера для решения СЛУ, условия их применимости.
8. Метод Гаусса решения СЛУ, условия его применимости. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ.
9. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы.
10. Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости.
11. Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ.
12. Понятие линейной независимости и зависимости частных решений однородной СЛУ. Фундаментальная система решений (ФСР), её нахождение. Представление общего решения однородной СЛУ через ФСР.
13. Минор 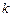 -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).
-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).
14. Понятие 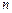 -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
15. Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.
16. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.
17. Понятие векторного пространства 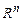 ,евклидова пространства
,евклидова пространства 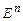 . Базис, канонический базис, ранг
. Базис, канонический базис, ранг 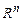 . Разложение вектора в
. Разложение вектора в 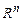 по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе.
по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе.
18. Понятие ортогональной системы векторов, ортогонального базиса. Нахождение координат вектора в ортогональном базисе.
19. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор.
20. Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. Нахождение собственных чисел и векторов оператора.
21. Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая, нормальная квадратичная форма. Закон инерции квадратичных форм.
22. Понятие знакоопределённости квадратичной формы. Главные миноры матрицы квадратичной формы. Критерии знакоопределённости квадратичной формы.
Раздел. Векторная алгебра и аналитическая геометрия.
23. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор.
24. Коллинеарность и компланарность векторов. Базис и канонический базис плоскости 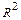 ; базис и канонический базис пространства
; базис и канонический базис пространства 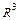 . Координаты вектора.
. Координаты вектора.
25. Понятие декартовой системы координат в 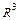 . Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
. Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
26. Преобразования прямоугольных декартовых систем координат на плоскости (параллельный перенос, поворот, зеркальное отражение). Связь между собой координат произвольной точки в старой и новой системах координат.
27. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами. Условие ортогональности векторов.
28. Векторное произведение векторов, его геометрический смысл и свойства. Выражение векторного произведения через координаты векторов. Условие коллинеарности векторов.
29. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов.
30. Понятие линии на плоскости. Общее уравнение линии и его нахождение по известному геометрическому свойству её точек. Окружность и её уравнение.
31. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Нахождение уравнения прямой, проходящей через точку перпендикулярно вектору. Построение прямой.
32. Каноническое уравнение прямой; уравнение прямой, проходящей через две точки; уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление, условия 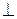 и ½½ прямых.
и ½½ прямых.
33. Понятие поверхности. Общее уравнение поверхности, его нахождение по известному геометрическому свойству её точек. Сфера и её уравнение.
34. Плоскость и её общее уравнение. Нормальный вектор плоскости и его нахождение. Уравнение плоскости, проходящей через точку перпендикулярно вектору. Построение плоскости.
35. Уравнение плоскости, проходящей через три точки; уравнение плоскости в отрезках. Расстояние от точки до плоскости. Угол между плоскостями и его вычисление, условия 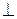 и ½½ плоскостей.
и ½½ плоскостей.
36. Понятие линии в пространстве и её общее уравнение. Понятие прямой линии в пространстве и её общее уравнение. Направляющий вектор прямой и его нахождение.
37. Каноническое уравнение прямой в пространстве; уравнение прямой, проходящей через две точки; параметрические уравнения прямой. Приведение общего уравнения к каноническому.
38. Угол между двумя прямыми в пространстве, между прямой и плоскостью и их вычисление, условия 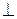 и ½½ двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости.
и ½½ двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости.
39. Кривая 2-ого порядка на плоскости и её общее уравнение. Классификация кривых 2-ого порядка. Приведение уравнения кривых к каноническому виду.
40. Эллипс. Каноническое уравнение эллипса. Построение эллипса. Вершины, полуоси, фокусы, эксцентриситет, общее геометрическое свойство точек эллипса.
41. Гипербола. Каноническое уравнение гиперболы. Построение гиперболы. Вершины, полуоси, фокусы, эксцентриситет, асимптоты, общее геометрическое свойство точек гиперболы.
42. Парабола. Каноническое уравнение параболы. Построение параболы. Вершина, фокус, эксцентриситет, директриса, общее геометрическое свойство точек параболы.
43. Сфера. Эллипсоид. Канонические уравнения и графики.
44. Гиперболоиды (однополостной и двуполостной). Канонические уравнения и графики.
45. Параболоиды (эллиптический и гиперболический). Канонические уравнения и графики.
46. Цилиндры (эллиптический, гиперболический, параболический), их уравнения и графики.
Приложения.
6.1. Образец решения контрольных задач типового варианта.
1 – 10.Вычислить определитель: 

а)непосредственным разложением по 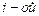 строке;
строке;
б)непосредственным разложением по 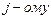 столбцу;
столбцу;
Решение. а)вычисляем определитель разложением по элементам первой строки: 
 =
=  .
.






Тогда  =
=  =
= 
б)вычисляем определитель непосредственным разложением по элементам
второго столбца: 
 =
=  .
.






Тогда  =
=  =
=  .
.
Ответ: 
 .
.
11-20.Найти матрицу ,если:
,если:
 ,
,  .
.
Решение:
1)Транспонируем матрицу :
:  .
.
2)Вычисляем произведение матриц  :
:


 .
.
3)Находим матрицу  :
:

 .
.
4)Находим матрицу  :
: 

 .
.
Ответ:  .
.
21 – 30. Дана система уравнений:  . Требуется:
. Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а)Вычисляем определитель системы и проверяем, что он отличен от нуля:

 .
.
2а) Так как  , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 
3а) Вычисляем определители  :
:

 ,
,

 ,
,

 .
.
4а) Находим решение:  .
.
5а) Выполняем проверку: 
 .
.
Ответ:  .
.
Б) Метод обратной матрицы.
1б)Записываем систему уравнений в матричном виде:
 или
или 
2б)Вычисляем определитель системы и проверяем, что он отличен от нуля:


3б) Так как  , то матрица системы
, то матрица системы  имеет обратную матрицу
имеет обратную матрицу  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой:
 или
или 
4б)Находим обратную матрицу  (методом присоединённой матрицы):
(методом присоединённой матрицы):
 .
.









Тогда  .
.
5б)Находим решение:
 .
.
6б) Выполняем проверку: 
 .
.
Ответ:  .
.
В) Метод Гаусса.
1в)Записываем расширенную матрицу системы:
 .
.
2в)Выполняем прямой ход метода Гаусса.
В результате прямого хода матрица системы  должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами  . Система уравнений, матрица которой
. Система уравнений, матрица которой  является треугольной с элементами
является треугольной с элементами 
 , имеет единственное решение, а система уравнений, матрица которой
, имеет единственное решение, а система уравнений, матрица которой  является трапециевидной с элементами
является трапециевидной с элементами 
 , имеет бесконечно много решений.
, имеет бесконечно много решений.








 .В результате элементарных преобразований матрица
.В результате элементарных преобразований матрица  системы преобразована к специальному виду
системы преобразована к специальному виду  . Система уравнений, матрица которой
. Система уравнений, матрица которой  , является треугольной с ненулевыми диагональными элементами
, является треугольной с ненулевыми диагональными элементами  , имеет всегда единственное решение, которое находим, выполняя обратный ход.
, имеет всегда единственное решение, которое находим, выполняя обратный ход.
Если при выполнение преобразования расширенной матрицы  в преобразованной матрице
в преобразованной матрице
