Функция распределения случайной величины и
Функция распределения случайной величины и
Ее основные свойства.
Определение. Пусть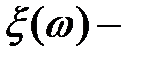 
случайная величина. Вещественная функция 
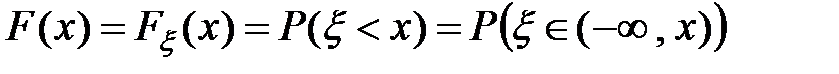, заданная на множестве всех вещественных чисел, называется функцией распределения случайной величины 
.
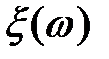Необходимо предположить, что события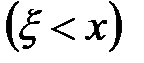 
попадают в выбранную 
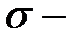алгебру событий 
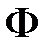для любого 
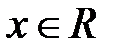,где 
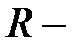множество вещественных чисел, так как вероятность события была введена только для событий, входящих в .
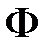Теорема 12.1. Пусть 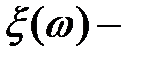случайная величина, 
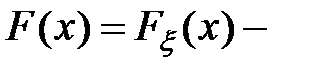функция распределения случайной величины 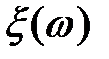. Тогда для любого 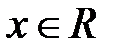верно неравенство 
.
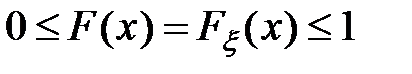Теорема 12.2. Пусть 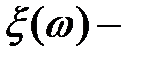случайная величина, 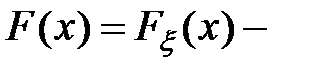функция распределения случайной величины 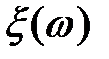. Тогда функция 
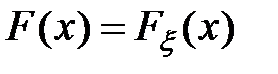неубывает всюду на 
.
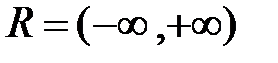Теорема 12.3. Пусть 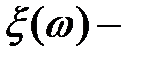случайная величина, 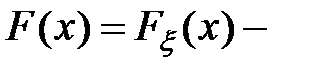функция распределения случайной величины 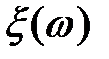. Пусть, кроме того
, 
.
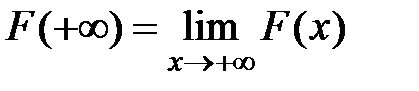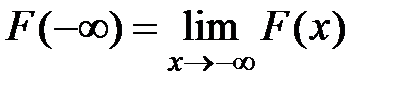Тогда верны равенства: 1)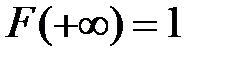 
; 2)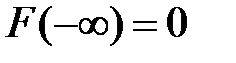 
.
Теорема 12.4 (о непрерывности функции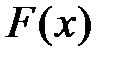 
слева). Пусть 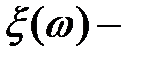случайная величина, 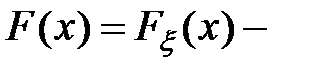функция распределения случайной величины 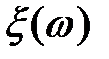. Пусть, кроме того, 
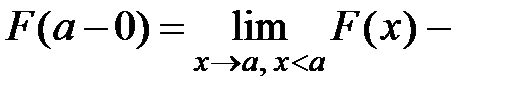левый односторонний предел функции 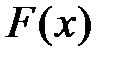в точке 
.
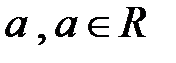Тогда верно равенство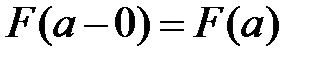 
.
Из теорем 2.1−2.4 следует, что график функции распределения 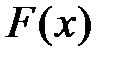выглядит примерно так:
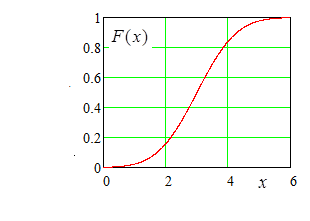
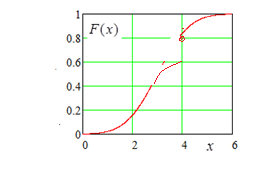
Замечание. Можно показать, что любая функция 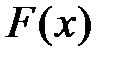, обладающая свойствами, указанными в теоремах 12.1−12.4, является функцией распределения некоторой случайной величины .
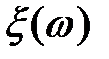Теорема 12.5 (о вероятности попадания случайной величины в промежуток). Пусть 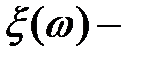случайная величина, 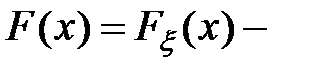функция распределения случайной величины 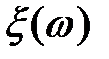. Пусть, кроме того, известно, что:
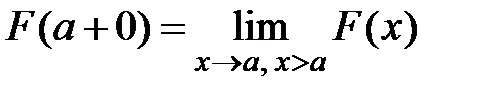и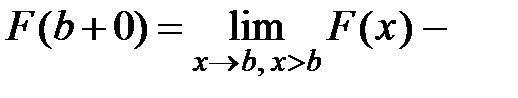 
правые односторонние пределы функции 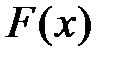в точках 
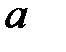и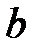 
соответственно, 
, 
, 
; 
, 
.
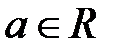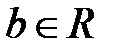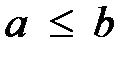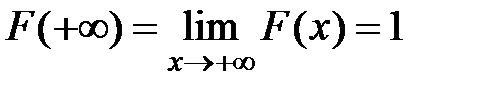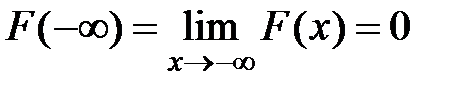Тогда верны равенства:
1) 
;
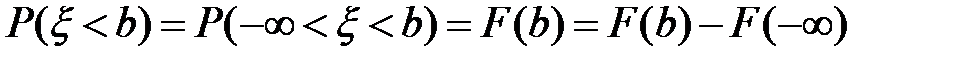2) 
;
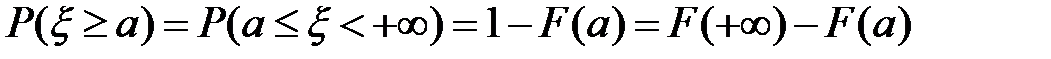3) 
;
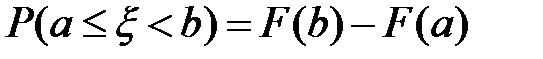4) 
;
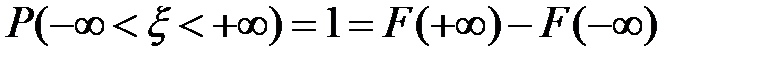5) 
;
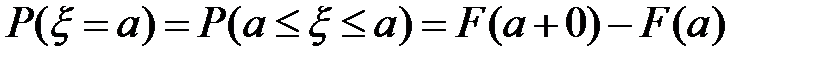6) 
;
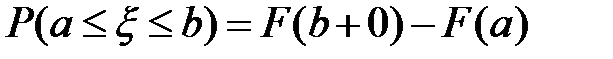7) 
;
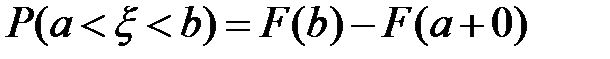8) 
;
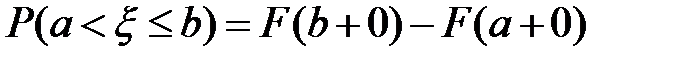9) 
;
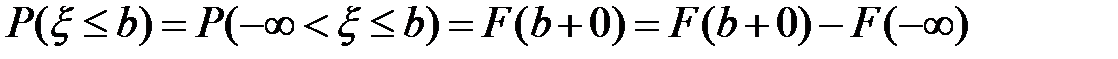10) 
.
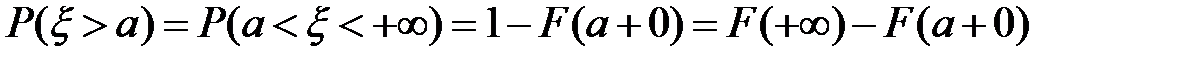Замечание. Полезно думать, что функция распределения случайной величины−это главная вероятностная функция случайной величины. С ее помощью можно найти многие числовые характеристики случайной величины. Поэтому часто, задавая случайную величину, указывают ее функцию распределения или любой объект, с помощью которого функция распределения однозначно восстанавливается. Этот объект, также как и саму функцию распределения, обычно называют законом распределения случайной величины. Надо добавить, что на практике функцию распределения случайной величины можно найти приближенно с помощью эмпирической функции распределения методами математической статистики. Для вычисления числовых характеристик случайной величины требуется хорошо знать теорию интегралов, конечных сумм, рядов (бесконечных сумм). Явно недостаточно использование определенного интеграла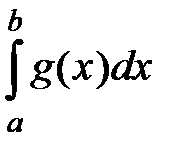 
и несобственных интегралов 
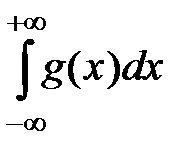и интегрирования по Риману. Из-за этого в традиционных курсах теории вероятностей для технических университетов отдельно изучаются дискретные случайные величины и непрерывные случайные величины. Это приводит к неполной теории случайных величин. Если применять интегралы Стильтьеса 
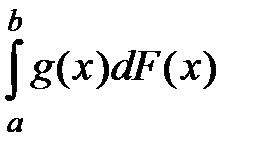или интегралы по мере (по вероятности) 
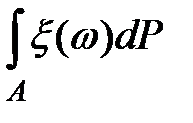, а также интегрирование по Лебегу, то все случайные величины можно изучать вместе и получается полная теория случайных величин. Такая теория рассматривается в серьезных курсах теории вероятностей
Функция распределения случайной величины и
Ее основные свойства.
Определение. Пусть 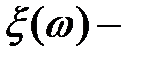случайная величина. Вещественная функция 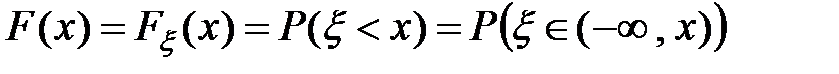, заданная на множестве всех вещественных чисел, называется функцией распределения случайной величины .
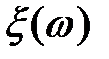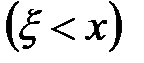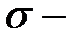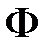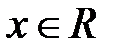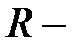Необходимо предположить, что события попадают в выбранную алгебру событий для любого ,где множество вещественных чисел, так как вероятность события была введена только для событий, входящих в .
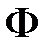Теорема 12.1. Пусть 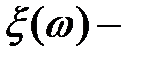случайная величина, 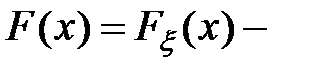функция распределения случайной величины 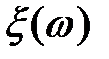. Тогда для любого 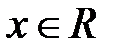верно неравенство .
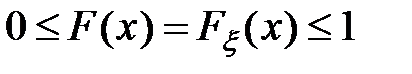Теорема 12.2. Пусть 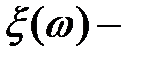случайная величина, 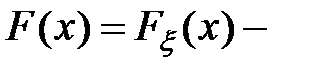функция распределения случайной величины 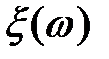. Тогда функция 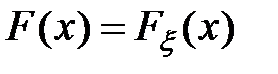неубывает всюду на .
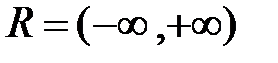Теорема 12.3. Пусть 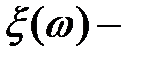случайная величина, 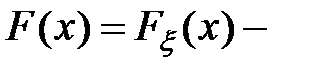функция распределения случайной величины 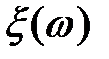. Пусть, кроме того
, .
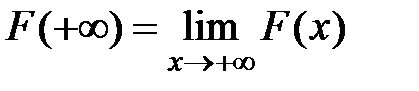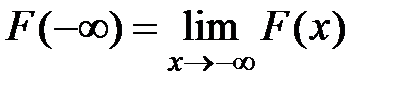Тогда верны равенства: 1) 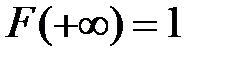; 2) .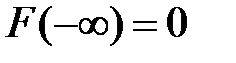
Теорема 12.4 (о непрерывности функции 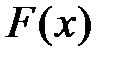слева). Пусть 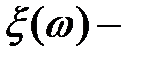случайная величина, 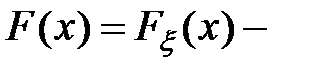функция распределения случайной величины 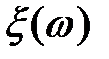. Пусть, кроме того, 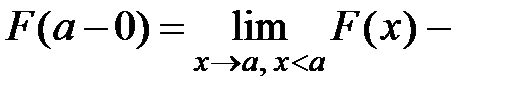левый односторонний предел функции 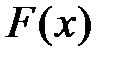в точке .
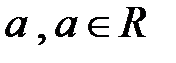Тогда верно равенство .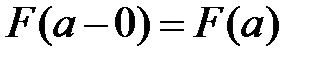
Из теорем 2.1−2.4 следует, что график функции распределения 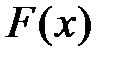выглядит примерно так:
Замечание. Можно показать, что любая функция 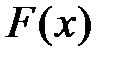, обладающая свойствами, указанными в теоремах 12.1−12.4, является функцией распределения некоторой случайной величины .
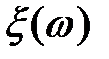Теорема 12.5 (о вероятности попадания случайной величины в промежуток). Пусть 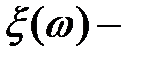случайная величина, 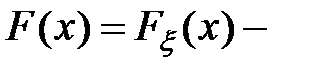функция распределения случайной величины 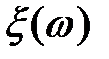. Пусть, кроме того, известно, что:
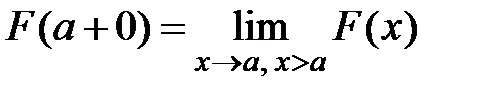и 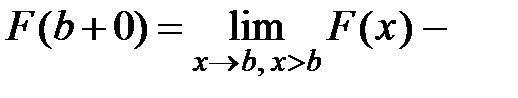правые односторонние пределы функции 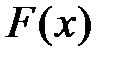в точках 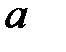и 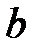соответственно, , , ; , .
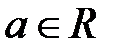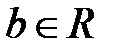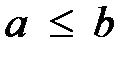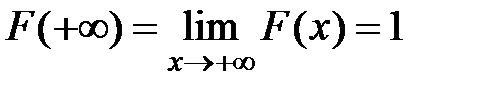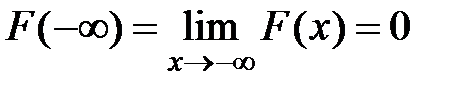Тогда верны равенства:
1) ;
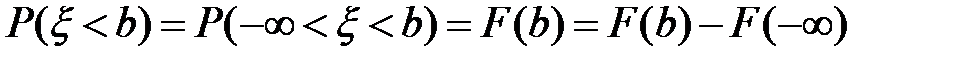2) ;
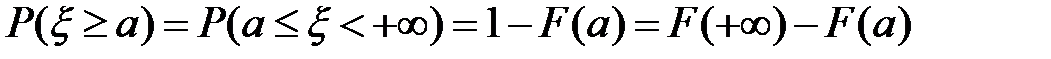3) ;
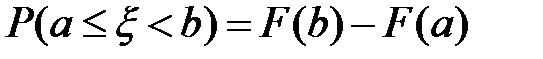4) ;
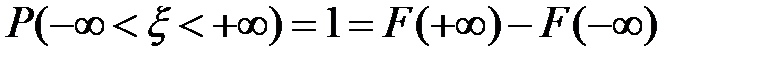5) ;
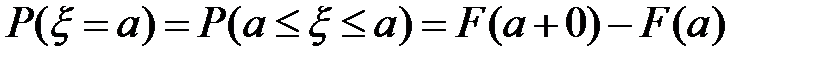6) ;
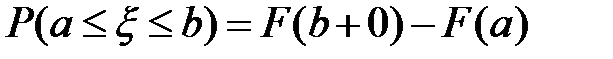7) ;
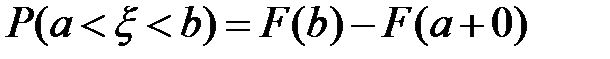8) ;
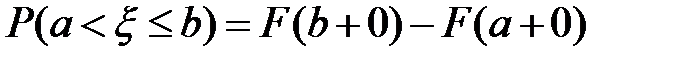9) ;
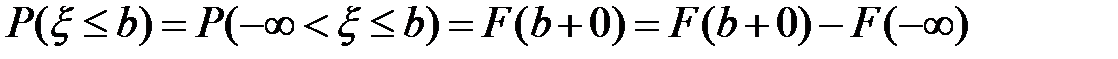10) .
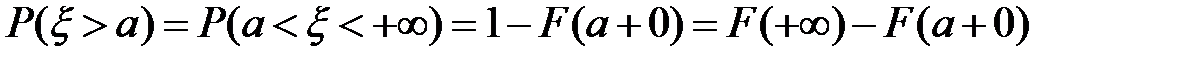Замечание. Полезно думать, что функция распределения случайной величины−это главная вероятностная функция случайной величины. С ее помощью можно найти многие числовые характеристики случайной величины. Поэтому часто, задавая случайную величину, указывают ее функцию распределения или любой объект, с помощью которого функция распределения однозначно восстанавливается. Этот объект, также как и саму функцию распределения, обычно называют законом распределения случайной величины. Надо добавить, что на практике функцию распределения случайной величины можно найти приближенно с помощью эмпирической функции распределения методами математической статистики. Для вычисления числовых характеристик случайной величины требуется хорошо знать теорию интегралов, конечных сумм, рядов (бесконечных сумм). Явно недостаточно использование определенного интеграла 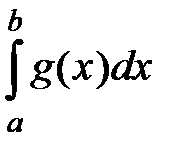и несобственных интегралов 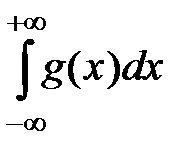и интегрирования по Риману. Из-за этого в традиционных курсах теории вероятностей для технических университетов отдельно изучаются дискретные случайные величины и непрерывные случайные величины. Это приводит к неполной теории случайных величин. Если применять интегралы Стильтьеса 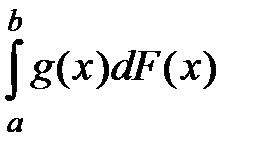или интегралы по мере (по вероятности) 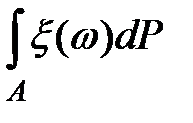, а также интегрирование по Лебегу, то все случайные величины можно изучать вместе и получается полная теория случайных величин. Такая теория рассматривается в серьезных курсах теории вероятностей