Метод «черного ящика» при изучении сложных систем

Метод основан на анализе «входов» для ввода информации и «выход» для отображения результатов работы. Состояние выходов обычно функционально зависит от состояния входов. В модель включается то, что существенно для достижения цели (целевое назначение модели)
вход→система→ выход(реакция, эффект, результат)

Метод Ч.Ящика. позволяет решать 3 вида задач:1)Прогностические задачи (есть чайник, значит на выходе кипяток) 2) Диагностические(доктор-пациент) 3)Общенаучные задачи самый встречаемый(азот-рост растений)

Модель «черного ящика» — модель системы, представляющая собой структуру с известными выходными и входными параметрами и неизвестным внутренним устройством. Исследуя известные параметры, с помощью такой модели можно получить представление о внутреннем устройстве.

Классификация используемых в системных исследованиях моделей

МоделиМатериальные:- Пространственно подобные объекту модели (глобус)-Модели физические, хим-ие, биолог-ие, (подобные объекту, аквариум)-Модели логически подобные объекту (комп. Логика)

Модели Идеальные:-вербальные (формулировка теорий). Математические делятся а)Пространственные(1или несколько пространств координат). Б)Точечная(таксы зависим. От вывозки древ). –Динамические(времен. Фактор). Статические(ход роста насаждений)

-Оптимизационные для поиска решений наиболее соответств-им предъявляем требованиям. Дискретивные – описательные модели(кривые высот) где D зависитoтh дерева.

Основные понятия корреляционного анализа. Коэффициент парной корреляции

Корреляция – это статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Различают парную, частную и множественную корреляцию.

Корреляционный анализ – это раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами. Корреляционный анализ заключается в количественном определении тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции. Построение коэффициентов корреляции основано на сумме произведений отклонений индивидуальных значений признаков x_i и y_i от их средних значений и :Парная корреляция – это связь между двумя признаками (результативным и факторным или между двумя факторными).

Коэффициентлинейнойкор. обладает следующими свойствами :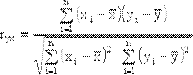

1) не имеет размерности, следовательно, сопоставим для величин различных порядков;

2) изменяется в диапазоне от –1 до +1. Положительное значение свидетельствует о прямой линейной связи, отрицательное – об обратной. Чем ближе абсолютное значение коэффициента к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент по абсолютной величине превышает 0,7, и слабая, если он менее 0,3.

Коэффициент множественной корреляции заключен в пределах 0 ≤ R ≤ 1. Он не меньше, чем абсолютная величина любого парного или частного коэффициента корреляции с таким же первичным индексом.

С помощью множественного коэффициента (по мере приближения R к 1) делается вывод о тесноте взаимосвязи, но не о ее направлении.

Частный коэффициент корреляции, так же как и парный коэффициент корреляции r (рассчитанный по формуле (6.4)), может принимать значения от -1 до 1

.

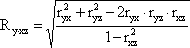При этом переменными могут быть данные тестирований, наблюдений, экспериментов, социально-демографические характеристики, физиологические параметры, особенности поведения и т. д. К примеру, использование метода позволяет нам дать количественно выраженную оценку взаимосвязи таких признаков, как: успешность обучения в вузе и степень профессиональных достижений по его окончании, уровень притязаний и стресс, количество детей в семье и качества их интеллекта, черты личности и профессиональная ориентация, продолжительность одиночества и динамика самооценки, тревожность и внутригрупповой статус, социальная адаптированность и агрессивность при конфликте...