Вычисляем средние характеристики.

а) Определяем среднюю выборочную :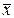

,

Вычисления оформим в виде таблицы:

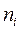12,8		12,8
13,6		27,2
14,4		129,6
15,2
16,0
16,8
18,4		18,4
		å=772

.

б) Определяем моду :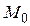

Для нашего примера модальным является пятый интервал, так как он имеет наибольшую частоту n₅=17, тогда:

.

в) Определяем медиану :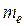

Для нашего примера медианным является четвертый интервал, так как его накопленная частота f₄=27 превышает половину объема выборки n=50, тогда:

.

Вычисляем характеристики вариации.

а) Определяем размах вариации :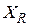

Найдем значение размаха вариации для наших результатов:

.

б) Определяем дисперсию D:

Вычисления оформим в виде таблицы:

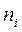12,8		-2,6	6,76	6,76
13,6		-1,8	3,24	6,48
14,4		-1,0	1,00	9,00
15,2		-0,2	0,04	0,60
16,0		0,6	0,36	6,12
16,8		1,4	1,96	9,80
18,4		3,0	9,00	9,00
				å=47,76

.

в) среднее квадратическое отклонение s:

.

г) Определяем коэффициент вариации V:

%= .

д) Определяем ошибку выборочного среднего : .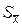

Вывод.По данным результатам бега на 100 м, показанным группой юношей 9 классов в составе 50 человек средний результат составил 15,4 с ± 0,1 с. Степень рассеяния данных выборки от среднего результата составляет 1,0 с. Чаще всего встречаемый результат в группе 15,7 с. Одна половина бегунов показала результаты лучше 15,5 с, а другая хуже. Отклонение результатов в беге на 100 м внутри группы составляют 5 с. Результаты исследования имеют малую варьируемость, что говорит об однородности выборки, а значит, средний результат типичен для рассматриваемого признака.

Пример 3

Задание:

1. Проверить гипотезу о нормальном распределении признака в генеральной совокупностис помощью критерия согласия Пирсона c² для уровня значимости a=0,05.

2. Построить нормальную кривую.

3. Сделать вывод.

Исходные данные: Бег 100м: 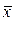=15,4, s = 0,9, h =0,8, n=50.

xi	12,8	13,6	14,4	15,2	16,0	16,8	17,6
ni

Этапы выполнения:

Проверим гипотезу о нормальном распределении результатов в беге на 100м.

1). Выдвигаем нуль-гипотезу.

H₀: результаты в беге на 100м в генеральной совокупности имеют нормальное распределение.

2). Определяем выравнивающие частоты.

Вычисления оформим в таблицу:

	12,8		-2,6	-2,89	0,0061	0,27
	13,6		-1,8	-2,00	0,0540	2,40
	14,4		-1,0	-1,11	0,2155	9,57
	15,2		-0,2	-0,22	0,3894	17,29
	16,0		0,6	0,54	0,3448	15,31
	16,8		1,4	1,56	0,1182	5,25
	17,6		2,2	2,44	0,0203	0,90

3). Определяем расчетное значение критерия c₀².

Вычисления также представим в виде таблицы:

		0,27	0,73	0,53	1,96
		2,40	-0,40	0,16	0,07
		9,57	-0,57	0,32	0,03
		17,29	-2,29	5,24	0,30
		15,31	-1,69	2,82	0,18
		5,25	-0,25	0,06	0,01
		0,90	-0,10	0,01	0,01
					S=2,56

Таким образом, c₀²=2,56.

4). Определяем число степеней свободы n = 7-3 = 4.

5). Находим критические значения критерия согласия c².

Для уровня значимости a=0,05 и числа степеней свободы n=4 имеем (приложение 3): c²(0,05;4)=9,49,

6). Проверяем гипотезу: сравниваем расчетное значение критерия c₀² с табличным значением c².

c₀²<c² (2,56<9,49)

Построим нормальную кривую.

Для построения нормальной кривой на оси OX откладывают значения x_i, а на оси OY – соответствующие значения выравнивающих частот n_i^’.

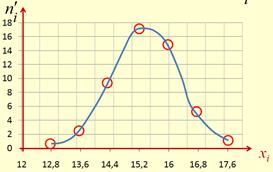
3. Вывод.Выдвинутая гипотеза о нормальном распределении результатов в беге на 100м у данных спортсменов принимается на уровне значимости 0,05, так как расчетное значение критерия согласия c₀²=2,56 меньше критического значения c2=9,49. Средний результат в беге на 100м в 95% случаев у обследуемых спортсменов находится в пределах от 15,2с до 15,6с, а дисперсия с вероятностью 0,95 не выйдет за границы 0,49 – 1,13.

Пример 4

Задание:

1. Сравнить по методу Фишера рассеивание показателей в контрольной и экспериментальной группах на уровне значимости a=0,05.

2. Сделать вывод.

Исходные данные: Гребля на каноэ 500м.

xэ,мин	2,00	1,69	2,12	2,10	2,15	1,78	2,30	1,80
xк,мин	2,20	2,25	2,40	2,20	2,05	2,50	2,40	2,10

Этапы выполнения:

1. Сравним по методу Фишера рассеивание показателей в контрольной и экспериментальной группах на уровне значимости a=0,05.

1). Выдвигаем нулевую гипотезу.

H₀: (D_э=D_к) – дисперсии результатов гребли на каноэ 500м в экспериментальной и контрольной группах не отличаются значимо.

2). Рассчитываем выборочные дисперсии результатов измерений.

Результаты вычислений оформим в виде таблицы:

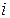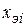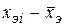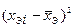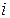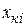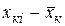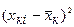	2,00	-0,12	0,01			2,20	-0,06	0,00
	1,69	-0,43	0,18			2,25	-0,01	0,00
	2,12					2,40	0,14	0,02
	2,10	-0,02	0,00			2,20	-0,06	0,00
	2,15	0,03	0,00			2,05	-0,21	0,04
	2,78	0,66	0,44			2,50	0,24	0,06
	2,30	0,18	0,03			2,40	0,14	0,02
	1,80	-0,32	0,10			2,10	-0,16	0,03
	S=16,94		S=0,76			S=18,10		S=0,17

, ,

,.

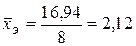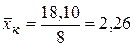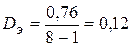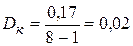3). Вычисляем расчетное значение F-критерия (Фишера).

Так как D_э>D_к Þ .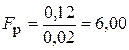

4). Находим число степеней свободы.

n_э=8-1=7, n_к=8-1=7.

5). По таблице (см. приложение 4) находим критическое значение F-критерия для уровня значимости a=0,05 и числа степеней свободы n_э=7, n_к=7:F(0,05;7;7)=3,8.

6). Проверяем гипотезу: сравниваем расчетное значение критерия F_р с табличным значением F (то есть, оцениваем достоверность различий выборочных совокупностей).

F_р > F (6,00>3,8)

Вывод.Таким образом, выдвинутая гипотеза отвергается на уровне значимости a=0,05, то есть с вероятностью 0,95 различие дисперсий существенно, что позволяет говорить о принадлежности дисперсий к разным генеральным совокупностям.

Пример 5

Задание:

1. Установить по методу Стъюдента (для несвязанных выборок) достоверность различия результатов в двух группах, занимающихся по различной методике (a=0,01).

2. Сделать вывод.

Исходные данные:Бег 60м.

x1,м	8,2	7,8	8,2	8,3	7,6	8,4	7,7	8,3
x2,м	9,2	8,9	8,6	9,0	7,9	8,7	8,6	8,8	9,1

Этапы выполнения:

1. Установим по методу Стъюдента (для несвязанных выборок) достоверность различия результатов в двух группах, занимающихся по различной методике (a=0,01).

1). Выдвигаем нулевую гипотезу.

H₀: ( 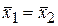) – средние выборочные значения результатов бега на 100м в экспериментальной и контрольной группах не отличаются значимо.

2). Рассчитываем значения выборочных характеристик , , , .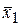

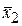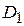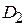Результаты вычислений оформим в виде таблицы:

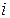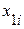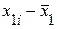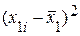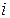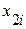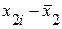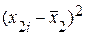	8,2	0,1	0,01			9,2	0,4	0,16
	7,8	-0,3	0,09			8,9	0,1	0,01
	8,2	0,1	0,01			8,6	-0,2	0,04
	8,3	0,2	0,04			9,0	0,2	0,04
	7,6	-0,5	0,25			7,9	-0,9	0,81
	8,4	0,3	0,09			8,7	-0,1	0,01
	7,7	-0,4	0,16			8,6	-0,2	0,04
	8,3	0,2	0,04			8,8
	S=64,5		S=0,69			9,1	0,3	0,09
						S=78,8		S=1,2

, ,

,.

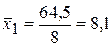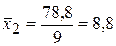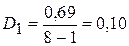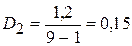3). Вычисляем расчетное значение t-критерия Стъюдента.

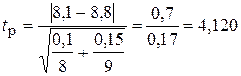
4). Находим число степеней свободы.

n=8+9-2=15.

5). По таблице (см. приложение 5) находим критическое значение t-критерия Стъюдента для уровня значимости a=0,01 и числа степеней свободы n=15:t(0,01;15)=2,947.

6). Проверяем гипотезу: сравниваем расчетное значение критерия t_р с табличным значением t (то есть, оцениваем достоверность различий выборочных совокупностей).

t_р>t (4,120>2,947)

Вывод.Таким образом, выдвинутая гипотеза отвергается на уровне значимости a=0,01, то есть с вероятностью 0,99 по средним результатам группы существенно отличаются, что позволяет говорить об эффективности проводимой во второй группе методике.

Пример 6

Задание: Определить по методу Стъюдента (для связанных выборок) изменилось ли состояние спортсменов по результатам, показанным ими с разрывом в 10 дней на уровне значимости a=0,001.

Исходные данные: Число отжиманий в упоре лежа.

x1, раз
x2, раз

Этапы выполнения:

Выдвигаем нулевую гипотезу.

H₀: ( 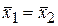) – средние выборочные результатов в отжиманиях в упоре лежа одинаковы, то есть значимо не отличаются.

2. Рассчитываем основные характеристики , :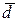

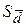Результаты вычислений оформим в виде таблицы:

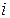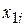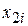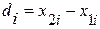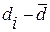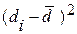				4,3	18,49
				4,3	18,49
				-2,7	7,29
				0,3	0,09
				-0,7	0,49
				-0,7	0,49
				-1,7	2,89
				-3,7	13,69
				0,3	0,09
			S=33		S=62,01

, , .
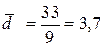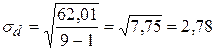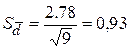