Задача 2: Корреляционно-регрессионная модель лесной экосистемы

Зависимость количества проросших семян (в группе из 10 шт.) цветочных растений от времени их хранения (лет)

Время хранения (х)											, α = 61
Количество проросших семян (у)

Порядок выполнения задачи:

1.Изобразить исходные данные графически в виде поля корреляции.

2.Построить линейное уравнение парной регрессии у от х. Расчет параметров уравнения провести в среде Mathсad.

3.Рассчитать коэффициент линейной корреляции, среднюю ошибку аппроксимации и F - критерий Фишера с помощью ППП Mathсad.

4.Оценить статистическую значимость параметров регрессии и корреляции. Дать анализ полученным результатам.

5.Выполнить прогноз количества проросших семян у при прогнозном значении времени их хранения х, составляющем a = 61% от среднего уровня.

6.С использованием MS Excel провести расчет параметров линейной регрессии с выводом дополнительной регрессионной статистики.

7.С помощью Excel построить графики исходных данных и линий регрессии: а) линейной; б) логарифмической; в) полиномиальной; г) степенной; д) экспоненциальной.

8.Выбрать наилучший вид линии регрессии на основании графического изображения и значения коэффициента детерминации.

Решение:

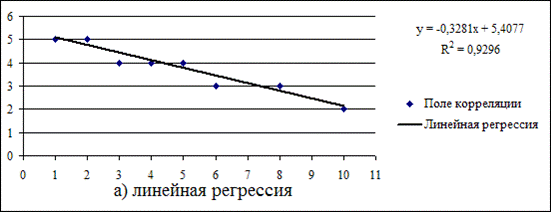
1.Изобразим исходные данные графически в виде поля корреляции, отмечая по оси абсцисс значения факторного признака х – время хранения семян (лет), а по оси ординат - результативного признака у – количество проросших семян (в группе из 10 шт.) цветочных растений (рисунок 9).

Рисунок 9

- точка поля корреляции ; ¾ - линия регрессии.

2.На основании вида поля корреляции будем считать, что корреляционная связь между количеством проросших семян, и временем их хранения прямолинейная, которая задается уравнением .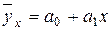

Для расчета параметров уравнения линейной регресси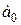и и 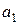воспользуемся таблицей 8, заполняя в ней сначала столбцы 1 – 6, а после того, как будет получено уравнение регрессии – остальные. Все вычисления производим с использованием Mathcad, рабочий документ, содержащий эти вычисления см. в приложении 7.

Для нахождения параметров 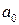и и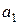спользуем систему уравнений, полученную по МНК (28):

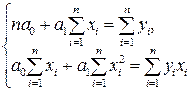тогда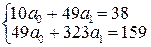

Решая эту систему уравнений по формулам Крамера в среде Mathcad, находим 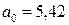и 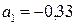. Следовательно, уравнение регрессии имеет вид:

.

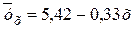Таблица 8 – Расчет параметров линейной регрессии

№ п/п	Исходные данные	Промежуточные данные	Проверка качества модели
		·
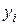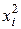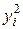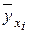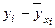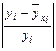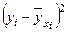						5.090	-0.090	0.018	0.008
						2.780	0.220	0.073	0.048
						4.430	-0.430	0.107	0.185
						3.770	0.230	0.058	0.053
						2.780	0.220	0.073	0.048
						2.120	-0.120	0.060	0.014
						4.760	0.240	0.048	0.058
						4.100	-0.100	0.025	0.010
						4.760	0.240	0.048	0.058
						3.440	-0.440	0.147	0.194
Итого						-	-	0,657	0,676
Среднее значение		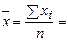	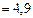		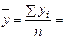	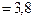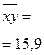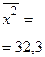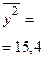-	-	0,0657	-
			-	-	-	-	-	-	-
			-	-	-	-	-	-	-

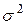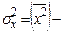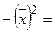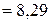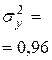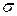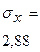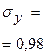3.Тесноту линейной связи оценивает коэффициент корреляции, который определим с использованием формулы (29) в Mathcad:

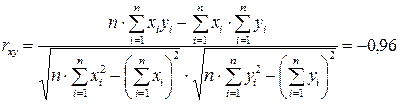
Определяем коэффициент детерминации: 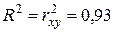, который указывает на то, что 93% вариации всхожести семян объясняется вариацией фактора х – временем их хранения.

Качество построенной модели оценивается также с помощью средней ошибки аппроксимации, определяемой по формуле (32), для использования которой заполняем столбцы 7 – 9, вычисляя 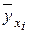путем подстановки в уравнение регрессии значения 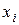. Тогда имеем:

.

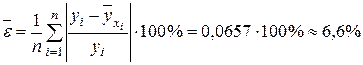Полученный результат указывает на хорошее качество модели, т.к. 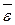не превышает 8 –15%.

Оценим статистическую значимость построенной модели по F– критерию Фишера, выдвинув гипотезу 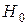о статистической незначимости уравнения регрессии и показателя тесноты связи.

Для этого рассчитаем фактическое значение критерия 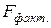по формуле (34): .

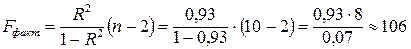Уровень значимости a принимаем равным 0,05 и определяем число степеней свободы факторной дисперсии 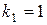(т.к. регрессия линейная) и остаточной дисперсии 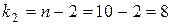. По таблице приложения 5 находим критическое значение критерия .

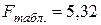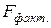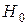Так как > , то – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность уравнения регрессии.

4.Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента.

Выдвигаем гипотезу 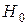о статистически незначимом отличии показателей от нуля: .

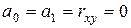Определяем табличное значение критерия Стьюдента 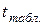для числа степеней свободы 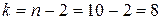и уровня значимости a = 0,05 по таблице приложения 1: 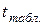=2,306.

Найдем случайные ошибки 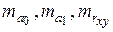, используя приведенные выше формулы (35)-(37) и данные таблицы 8 (см. программу Mathcad):

,

,

.

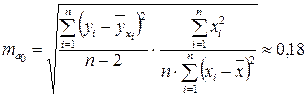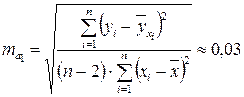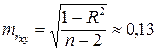Тогда определяем фактические значения t-статистики по формулам (38):

.

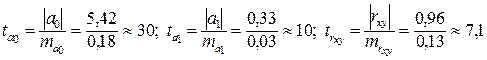Так как фактические значения t-статистики превосходят табличное значение для каждого показателя: 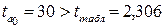; ; 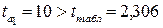, то гипотеза 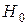отклоняется, т.е. 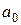, 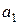и 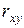не случайно отличаются от нуля, а статистически значимы. Следовательно, полученное уравнение линейной регрессии 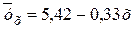статистически достоверно. Строим линию регрессии на рисунке 9 (сплошная линия).

Коэффициент 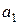= – 0,33 в уравнении регрессии означает, что с увеличением срока хранения на 1 год, всхожесть семян уменьшается на 0,33.

Если же считать, что х = 0 (в условиях данной задачи это возможно, т.е. семена не хранили, а стали проращивать сразу же после сбора), то средняя всхожесть составит 5,42 шт. в группе из 10 семян. Так как 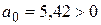, то изменение всхожести идет медленнее, чем изменение сроков хранения .

5. Полученное уравнение регрессии может быть использовано для прогноза.

По условию прогнозное значение всхожести составляет 61% от среднего уровня, т.е.: 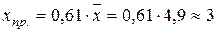, тогда прогнозное значение среднего срока хранения составит: 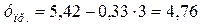(лет).

6. Встроенная статистическая функция ЛИНЕЙН в Excel определяет параметры линейной регрессии 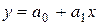. Порядок вычислений следующий:

а) открыв Excel вводим исходные данные по столбцам, считая, что факторный признак х – это срок хранения, а результативный признак у – количество проросших семян;

б) выделим область пустых ячеек 5 ´ 2 (5 строк, 2 столбца) рядом с исходными данными для вывода результатов регрессионной статистики;

в) выбираем на панели задач Формулы / Другие формулы / Статистические /ЛИНЕЙН (рисунок 10);

г) заполняем аргументы функции (рисунок 11).

Известные _значения_у – диапазон, содержащий данные результативного признака. Чтобы ввести в качестве аргумента ссылку на ячейку, щелкнем значок , чтобы временно закрыть диалоговое окно. Выбрав ячейки на рабочем листе, щелкнем значок .

Известные_значения_х – диапазон, содержащий данные факторного признака, который вводится аналогично как и для у.

Константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении регрессии: если Константа = 1, то свободный член 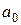рассчитывается обычным образом, если Константа = 0, то свободный член равен 0. Вводим 1.

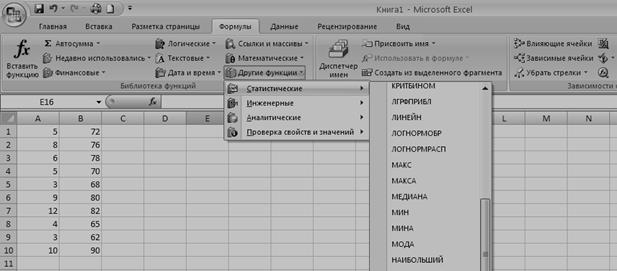
Рисунок 10 – Диалоговое окно «Формулы»

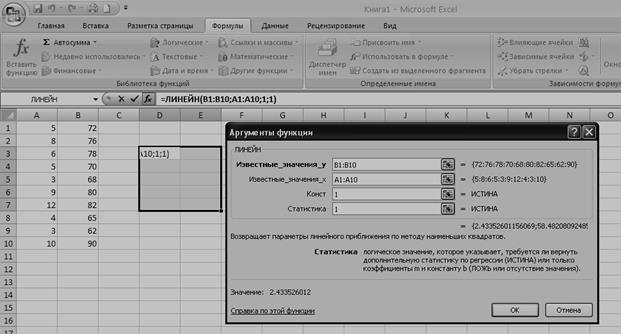
Рисунок 11 – Диалоговое окно ввода аргументов функции ЛИНЕЙН

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика= 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения. Вводим 1. Щелкаем по кнопке Ок.

д) в левой верхней ячейке выделенной области появляется первый элемент итоговой таблицы.

Чтобы раскрыть всю таблицу, нажимаем на клавишу <F2>, а затем – на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.

Дополнительная регрессионная статистика выводится в порядке, указанном в следующей схеме:

Значение коэффициента	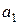Значение коэффициента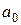
Среднеквадратическое отклонение	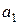Среднеквадратическое отклонение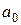
Коэффициент детерминации	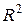Среднеквадратическое отклонение у
F – статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для данной задачи результат вычисления функции ЛИНЕЙН представлен на рисунке 12.

	Таблица значений факторного и результативного признаков
x
y
	-0,32811	5,40772
	0,03191	0,18138
	0,92963	0,29058
	105,691
	8,92449	0,67551

Рисунок 12 – Результат вычисления функции ЛИНЕЙН.

Сравнивая полученные значения с рассчитанными в Mathcad, убеждаемся в правильности проведенных вычислений.

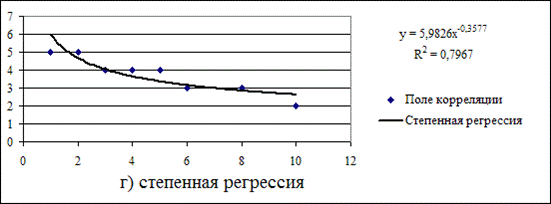
7. С использованием MS Excel построим графики исходных данных и линий регрессии: а) линейной; б) логарифмической; в) полиномиальной; г) степенной; д) экспоненциальной.

Построение графиков в Excel осуществляется с помощью Мастера диаграмм.

Для графического изображения исходных данных:

а) выделяем область исходных данных;

б) в главном меню выбираем Вставка / Точечная(Рисунок 13);

в) заполняем параметры диаграммы: названия диаграммы и осей, значения осей, линии сетки, параметры легенды и подписи данных. Макет / Название диаграммы; Макет/Название осей/Название основной горизонтальной (вертикальной) осей… .

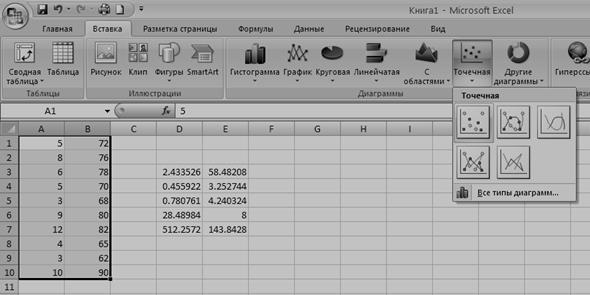
Рисунок 13 – Диалоговое окно Мастера диаграмм: тип диаграммы

г) В MS Excel может быть добавлена в диаграмму линия регрессии (тренда). Для этоговыделяем область диаграммы, затем на панели инструментов Макет/ Линия тренда/Дополнительные параметры линии тренда.В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение коэффициента детерминации, установив соответствующие флажки на закладке Формат линии тренда.

Образец рабочего документа Excel представлен далее (рисунок 14).

	Таблица значений факторного и результативного признаков
x
y

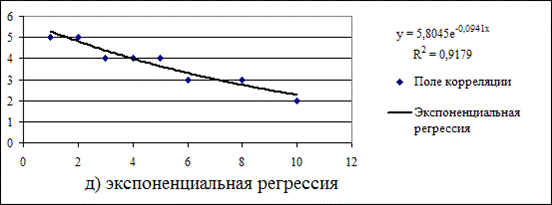Рисунок 14

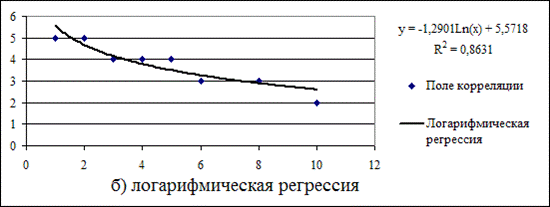
Для выбора наилучшего вида линии регрессии сравним значения коэффициента детерминации :

- линейная регрессия: = -0,3281x + 5,4077 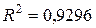(рисунок 14);

- логарифмическая регрессия: 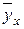= -1,2901Ln(x) + 5,5718,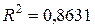

- квадратичная (полиномиальная, 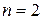) регрессия: 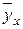= 0,0035x² - 0,3657x + 5,4789, ;

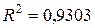- степенная регрессия: 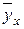= 5,9826x^-0,3577, ;

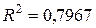- экспоненциальная регрессия y = 5,8045e^-0,0941x, R² = 0,9179.

8. Сравнивая коэффициенты детерминации у полученных линий тренда, отмечаем, что исходные данные лучше всего описывает квадратичная регрессия ( 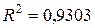). Следовательно, в данной задаче для расчета прогнозных значений следует использовать уравнение: 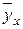= 0,0035x² - 0,3657x + 5,4789.