Однофакторный дисперсионный анализ в MS Excel

Для рассмотрения однофакторного дисперсионного анализа в MS Excel решим следующий пример.

Пример 3.2.В таблице 3 приведены данные по объемам работ, выполненных на посадке декоративных кустарников за смену для четырех бригад.

Таблица 3.

Номер бригады	Объем выполненной работы	Групповое среднее	Выборочная смещенная дисперсия
	140, 144, 142, 145	142,75	3,688
	150, 149, 152, 152	150,75	1,688
	148, 149, 146, 147	147,50	1,25
	150, 155, 154, 152	152,75	3,688

Проверить гипотезу дисперсионного анализа H₀ о равенстве средних: m₁ = m₂ = m₃ = m₄.

Решение. Для проверки гипотезы H₀ вычислим суммы Q₁ и Q₂ .

Общее выборочное среднее равно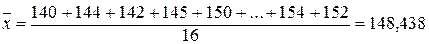

Тогда

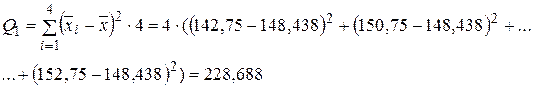
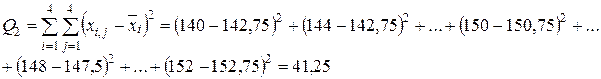
Вычислим статистику Фишера: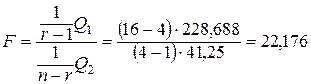

По таблицам распределения Фишера для a = 0,05 и степеней свободы k₁ =3, k₂ = 12 найдем критическое значение F_кр =3,49. Так как F> F_кр, то гипотезу H₀ отклоняем, т.е. считаем, что объем ежедневной выработки зависит от работающей бригады. Оценим степень этой зависимости с помощью коэффициента детерминации. Для этого вычислим Q :

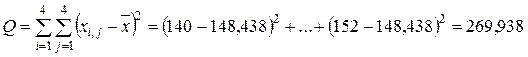
Контроль: Q = Q₁+Q₂ = 228,688 + 41,25 = 269,9 – верно!

По формуле (48) получим: 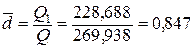, это означает, что 84,7% общей вариации (изменчивости) ежесменного объема выработки связано с работающей бригадой.

В MS Excel для проведения однофакторного дисперсионного анализа использует­ся процедура Однофакторный дисперсионный анализ.

Для проведения дисперсионного анализа необходимо:

•ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соот­ветствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора,

•выполнить команду Сервис > Анализ данных;

•в появившемся диалоговом окне Анализ данныхв списке Инструментыанализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;

•в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

•в разделе Группировка переключатель установить в положение по столбцам;

•указать Выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кноп­кой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верх­нюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведе­но сообщение в случае возможного наложения выходного диапазона на исход­ные данные.

•нажать кнопку ОК.

Результаты анализа. Выходной диапазон будет включать в себя результаты дис­персионного анализа: средние, дисперсии, критерий Фишера и другие показатели.

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Строка 1			142,75	4,916667
Строка 2			150,75	2,25
Строка 3			147,5	1,666667
Строка 4			152,75	4,916667
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	228,6875		76,22917	22,17576	3,48104E-05	3,490294821
Внутри групп	41,25		3,4375
Итого	269,9375

Как видно из таблицы, общая сумма квадратов SS (Q) = 269,938 разбита на компоненты: Q₁= 228,688, обусловленную различием средних значений между группами и Q₂= 41,25, обусловленную внутригрупповой изменчивостью

SS (Q)= Q₁+Q₂ ,

где Q- общая сумма квадратов отклонений наблюдений от общего среднего, Q₁- сумма квадратов отклонений выборочных средних от общего среднего, Q₂- сумма квадратов отклонений наблюдений от групповых средних.

Заметим, что MS в этой таблице есть средний квадрат, равный SS, деленная на число степеней свободы (df).

MS₁ = Q₁/ df₁ = 228,688 / 3 = 76,229

MS₂ = Q₂/ df₂ = 41,25 / 12 = 3,438

F = MS₁ / MS₂ = 76,229 / 3,438 = 22,176

Внутригрупповая изменчивость (SS) обычно называется остаточной компонентой или дисперсией ошибки. Это означает, что обычно при проведении эксперимента она не может быть предсказана или объяснена. С другой стороны, SS эффект (или компоненту дисперсии между группами) можно объяснить различием между средними значениями в группах. Иными словами, принадлежность к некоторой группе объясняет межгрупповую изменчивость, т.к. нам известно, что эти группы обладают разными средними значениями.
Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперси­онный анализ на пересечении строки Между группами и столбца Р-Значение. В случаях, когда Р-Значение < 0,05, критерий Фишера значим, и влияние исследуемого фак­тора можно считать доказанным.

Выводы:Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.