Разложение суммы квадратов отклонений

Несмещенной оценкой для неизвестной дисперсии σ² является, как известно, сумма квадратов

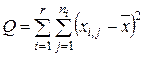, (40)

деленная на n - 1, где

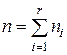(41)

количество всех наблюдений.

Основная идея дисперсионного анализа заключается в разбиении этой суммы квадратов отклонений на несколько компонент, каждая из которых соответствует предполагаемой причине изменения средних значений m_i .

Обозначим через

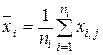(42)

- среднее арифметическое величин i-й группы, через

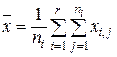(43)

- среднее арифметическое всех величин. Тогда справедливо тождество

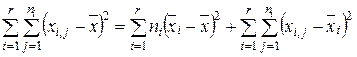, (44)

или Q = Q₁ + Q₂ . (45)

Таким образом, полная сумма квадратов отклонений от общего среднего Q разбивается на две компоненты: Q₁ - сумма квадратов между группами, Q₂ - сумма квадратов внутри групп. Если поделить обе части равенства (44) на число наблюдений n, то получим известное правило сложения дисперсий:

D_ОБЩ = D_ВНГР + D_МЕЖГР ,

где , ,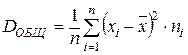

,

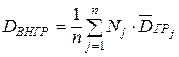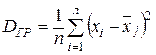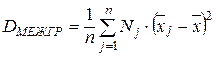
Пример 3.1. Дана совокупность, состоящая из следующих двух групп:

x				n1			n2	n
Частота

Необходимо доказать, что D_ОБЩ = D_ВНГР+ D_МЕЖГР.

Решение. Дано: n₁ = 10, n₂ = 9.

Найдем групповые средние: , .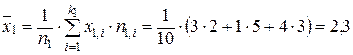

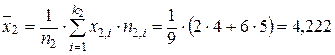Найдем групповые дисперсии: ,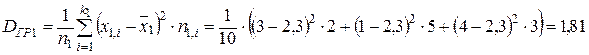

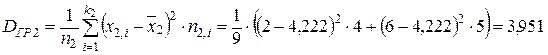
Найдем внутригрупповую дисперсию: .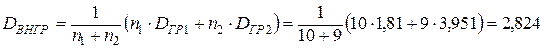

Найдем общую среднюю: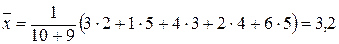

Найдем общую дисперсию: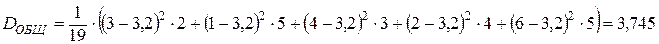

Найдем межгрупповую дисперсию: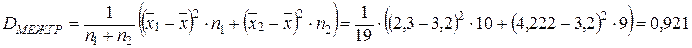

Убедимся, что общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий: D_ОБЩ= D_ВНГР +D_МЕЖГР = 2,824 + 0,921 = 3,745, что и требовалось показать.

Проверка гипотезы о равенстве групповых средних

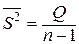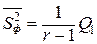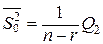Пусть гипотеза H₀: m_i = m, i =1,…r. Заметим, что величина , являющаяся несмещенной оценкой для σ² , всегда будет иметь распределение χ² с n - 1 степенями свободы и по ней можно построить доверительный интервал для σ² . Если гипотеза H₀ верна, то величины и (46)

будут иметь распределение Фишера с r-1 и n - r степенями свободы, соответственно, при этом 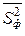и 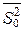являются несмещенными оценками для межгрупповой дисперсии 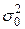. Отношение 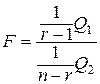- называется дисперсионным отношением и, если гипотеза H₀ верна, то статистика F имеет распределение Фишера с r -1, n - r степенями свободы. В этом случае эффекты влияния уровней фактора A будут нулевыми, т.е. m₁= m₂= ... =m_r = 0, а оценка параметра a равна общему среднему 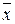, вычисленному по формуле (43). Проверка гипотезы H₀ о равенстве групповых средних проводится по схеме, изложенной ранее. Если же гипотеза H₀ отвергается, то параметр a по-прежнему вычисляется по формуле (43), а оценка эффекта m_i влияния i-го уровня фактора равна

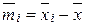, (47)

где 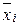определяется по формуле (44), а 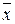- по формуле (43). Проверка гипотезы H₀ о равенстве групповых средних проводится по схеме, изложенной ранее.

Коэффициент детерминации

Предположим, что фактор A влияет на результативный признак X. Для измерения степени этого влияния используют выборочный коэффициент детерминации, равный

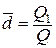, (48)

который показывает, какую долю выборочной дисперсии составляет дисперсия групповых средних, иначе говоря, какая доля общей дисперсии объясняется зависимостью результативного признака X от фактора A .

Сводка формул

Изложенные выше формулы для решения задач однофакторного анализа приведем в таблице 2. При вычислении сумм квадратов Q , Q₁ , Q₂ часто удобно при n_i = n₀ использовать следующие формулы:

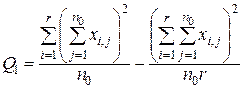, (49)

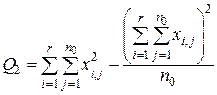, (50)

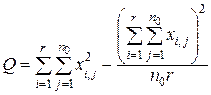. (51)

Таблица 2

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Оценки дисперсии
Межгрупповая		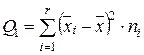r-1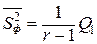
Внутригрупповая		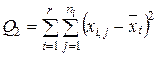n-r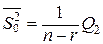
Общая		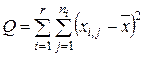n-1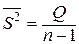