Тема 3. «Контроль и оценка знаний и умений учащихся по математике

Базовый уровень

Интеллектуальная разминка.

Обсуждение вопросов:

1. Цели, функции и принципы контроля и оценки знаний, умений и навыков младших школьников

2. Виды контроля, формы и средства проверки усвоения учебного материала по математике

3. Преимущества и недостатки каждой формы контроля.

4. Пути совершенствования контроля и оценки знаний, умений и навыков младших школьников

Заслушивание и обсуждение практических разработок студентов:

1. Электронная презентация проблемы: «Цели, функции и принципы контроля и оценки знаний, умений и навыков младших школьников»

2. Электронная презентация на тему: «Виды контроля, формы и средства проверки усвоения учебного материала по математике»

3. Устное сообщение на тему: «Методы диагностики образовательных достижений младших школьников»

4. Устное сообщение на тему: «Современные методы контроля и оценки математических знаний, умений и навыков младших школьников»

Составить аналитический обзор:

1. Используя различные источники информации (специализированные научные журналы, интернет) подготовьте обзор по теме «Нормы оценки знаний, умений и навыков в 1-4 классах»

2. Разработайте примерный вариант контрольной работы по математике и схему ее анализа

3. Подготовить сообщение по теме: «Преимущества и недостатки традиционных форм контроля»

4. Подготовить выступление на педагогическом совете школы на тему: «Пути совершенствования контроля и оценки знаний, умений и навыков младших школьников на уроках математики».

Повышенный уровень

Заслушивание и обсуждение сообщений на темы:

1. Функции контроля.

2. Планируемые образовательные результаты освоения основной образовательной программы.

3. Современные методы контроля и диагностики уровней достижения планируемых образовательных результатов.

4. Традиционные и инновационные формы контроля и диагностики образовательных результатов.

Составить аналитический обзор:

1. Используя различные источники информации (специализированные научные журналы, интернет) подготовьте обзор по теме «Формирование навыков самоконтроля и самооценки у младших школьников на уроках математики»

2. Составьте глоссарий по данной теме (10-15 терминов).

3. Проанализируйте практику организации контрольно-оценочной деятельности на уроках математики в начальной школе.

4. Подготовьте презентацию на тему: «Контроль знаний учащихся как основной элемент оценки качества образования

Подведение итогов практического занятия и объявление оценок.

Литература: основная 1-3, дополнительная 4-8.

Практическое занятие 4

Тема 4 Формирование у младших школьников универсальных учебных действий (УУД) на уроках математики.

Базовый уровень

Интеллектуальная разминка.

Обсуждение вопросов:

1. Развитие учащихся начальной школы в процессе обучения математике

2. Предметные и метапредметные результаты изучения математики в начальной школе.

3. Понятие и перечень основных универсальных учебных действий(УУД), которыми должен овладеть младший школьник (коммуникативные, регулятивные, личностные, познавательные) на уроках математики.

4. Развитие логических умений и навыков средствами математики в начальной школе.

Заслушивание и обсуждение сообщений на темы:

1. Электронная презентация проблемы: «Развитие учащихся начальной школы в процессе обучения математике»

2. Электронная презентация на тему: «Развитие логических умений и навыков младших школьников на уроках математики»

3. Устное сообщение на тему: «Достижение метапредметных результатов обучения с использованием предметного содержания математики в начальной школе»

4. Устное сообщение на тему: «Развитие универсальных учебных действий младших школьников при решении текстовых задач»

Составить аналитический обзор:

1. Выделите из «Федерального государственного образовательного стандарта начального общего образования» понятие и перечень основных универсальных учебных действий(УУД), которыми должен овладеть младший школьник (коммуникативные, регулятивные, личностные, познавательные)

2. Выберите из текста примерной программы по математике характеристику каждой группы УУД . Как они связаны с метапредметными результатами изучения математики?

3. Составить обзор способов развития мышления младшего школьника на уроках математики, раскрытых Н.Б.Истоминой [1, глава 3].

4. Подготовить выступление на педагогическом совете на тему:» Формирование универсальных учебных действий младших школьников на уроках математики в начальной школе.

Повышенный уровень

Заслушивание и обсуждение сообщений на темы:

1. Особенности формирования УУД младших школьников в системе учебников математики «Школа 2100»

2. Формирование УУД младших школьников в системе учебников математики развивающего обучения Л.В.Занкова

3. Формирование УУД младших школьников в системе учебников математики «Школа России»

4. Технологии формирования познавательных УУД на уроках математики.

Составить аналитический обзор:

1. Выделите основные направления развития личности младшего школьника на уроках математики, раскрытые Н.Б.Истоминой [1, глава 3].

2. Составить глоссарий (10-15 терминов) по теме.

3. Проанализируйте опыт работы начальной школы по формированию УУД на уроках математики.

4. Подготовьте презентацию на тему: « Способы достижения метапредметных планируемых результатов освоения основной образовательной программы при изучении курса математики в начальной школе»

Подведение итогов практического занятия и объявление оценок.

Литература: основная 1-3, дополнительная 4-8.

5.2. Перечень вопросов для повторения студентами изученного учебного материала по учебной дисциплине.

1. Предмет, задачи и цели изучения курса методики преподавания математики в вузе.

2. Математические понятия и способы действий.

3. Терминология и способы формирования понятий.

4. Последовательность изучения понятий в начальном курсе математики.

5. Урок математики и его особенности. Требования к современному уроку.

6. Связь методов, средств и организационных форм обучения с образовательными, воспитательными и развивающими задачами урока математики.

7. Проверка и оценка знаний, умений, навыков.

8. Домашние задания: организация, руководство и контроль.

9. Внеклассная работа по математике.

10. Реализация основных положений теории учебной деятельности в процессе обучения младших школьников математике.

11. Приёмы умственных действий и их формирование у младших школьников при обучении математике

12. Развитие логического и алгоритмического мышления младших школьников.

13. Методика изучения нумерации целых неотрицательных чисел;

14. Методика первичного ознакомления с арифметическими действиями (сложения, вычитания, умножения и деления);

15. Методика ознакомления учащихся со свойствами арифметических действий;

16. Устные приемы сложения и вычитания, умножения и деления по концентрам.

17. Понятие «задача» в начальном курсе математики;

18. Основные этапы работы над задачей.

19. Методы и способы решения текстовых задач.

20. Понятие математического выражения и выражения с переменной, равенства и неравенства, уравнения.

21. Методика ознакомления с алгебраическим материалом.

22. Методика ознакомления с геометрическим материалом.

23. Методика обучения младших школьников основным и производным величинам. Действия с величинами.

24. Изучение мер и формирование измерительных навыков.

25. Методика формирования у детей представлений о массе, емкости, единицы измерения и их соотношение.

26. Методика изучения мер длины и формирования навыков измерения.

27. Методика изучения темы «Площадь».

28. Методика формирования у детей временных представлений, изучения мер времени и их соотношений.

29. Методика ознакомления учащихся с дробями. Обучение решению задач с дробями.

30. Методика изучения долей. Обучение решению задач на нахождение доли числа и числа по его доле.

31. Организация самостоятельной работы на уроках математики.

32. Анализ различных концепций построения начального курса математики.

33. Проблемное обучение на уроках математики

34. Приемы активизации познавательной деятельности на уроках математики

35. Индивидуальный подход к обучению на уроках математики

Повышенный уровень.

1. Метапредметные и предметные планируемые результаты обучения математики согласно требованиям ФГОС

1. Учет и оценка знаний и умений учащихся как средство обратной связи и стимулирования деятельности учащихся
2. Внеклассная работа в начальной школе как средство формирования интереса к математике».
3. Организация самостоятельной работы учащихся на уроках математики в зависимости от выбора методов и приемов обучения
4. Средства обучения математике как компонент методической системы начального обучения
5. Современные программы обучения математике в условиях вариативного образования.
6. Моделирование как универсальное учебное действие при решении текстовых задач.

8. Сравнительный анализ альтернативных программ по математике в начальных классах (Модель «Начальная школа 21 века» «Школа 2000…» - «Школа 2100» «Гармония», система Л.В. Занкова и система Д.Б. Эльконина – В.В. Давыдова.).

9. Анализ различных концепций построения начального курса математики.

10. Проблемное обучение на уроках математики

11. Приемы активизации познавательной деятельности на уроках математики

12. Индивидуальный подход к обучению на уроках математики

13. Внеклассная работа по математике.

14. Реализация основных положений теории учебной деятельности в процессе обучения младших школьников математике.

15. Приёмы умственных действий и их формирование у младших школьников при обучении математике

16. Развитие логического и алгоритмического мышления младших школьников.

ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩИХСЯ ПО ДИСЦИПЛИНЕ

В период самостоятельной работы по освоению дисциплины «Методика преподавания математики в начальной школе» студенты по каждой теме учебно-тематического плана должны:

- изучать тексты учебников и учебных пособий;

- работать со словарями и справочниками;

- просматривать видео-лекцию;

- изучать учебные пособия из электронных библиотек (библиотека КИС «РосНОУ», ЭБС IPR books);

- готовить доклады и сообщения к семинарскому или практическому занятию;

- решать учебно-профессиональные задачи к практическому занятию;

- выполнять знаково-символические модели изучаемых явлений и готовят пояснения к ним;

- готовятся к деловым играм и тренингам;

- готовить материалы к «интеллектуальным разминкам» и «мозговым штурмам»;

- ответы на контрольные вопросы;

- аналитическая обработка текста (аннотирование, рецензирование, реферирование, контент-анализ и др.).

6.1. Практические задания для формирования профессиональных знаний

БАЗОВЫЙ УРОВЕНЬ (ПК-1-БЗ)

Задания:

6.1.1 (ПК-1-БЗ-1)

Найдите в программе математике М.И. Моро и др., программе Н.Б. Истоминой, программе Л.Г. Петерсон время и место изучения сочетательного, переместительного и распределительного свойства умножения; правил деления суммы на число и деления произведения на число.

6.1.2. (ПК-1-БЗ-1)

Найдите в программе математике М.И. Моро и др., программе Н.Б. Истоминой, программе Л.Г. Петерсон время и место изучения правил деления суммы на число и деления произведения на число.

6.1.3.(ПК-1- БЗ-2) Какие задания предлагаются в учебнике математики для 1 класса для объяснения смысла сложения и вычитания. Выпишите эти задания.

6.1.4.(ПК-1-БЗ-2) Какое свойство вычитания лежат в основе объяснения вычитания разрядных чисел?

6.1.5.(ПК-1-БЗ-3) Какое свойство вычитания лежат в основе объяснения вычитания 6.1.6.(ПК-1-БЗ-3) однозначного числа из двузначного с переходом через разряд?

Какие свойство вычитания лежат в основе объяснения, устного вычитания двузначного числа из двузначного с переходом через разряд?

6.1.7.(ПК-1-БЗ-4)

Приведите 3 вида простых арифметических задач, раскрывающих конкретный смысл действия сложения.

6.1.8. (ПК-1-БЗ-4)

Как предлагается объяснять смысл сложения и вычитания в учебники для 1 класса М.И. Моро и др. (рис. ).

Рис.

6.1.9. (ПК-1-БЗ-5)

Подготовьте для учащихся объяснение взаимосвязи сложения и вычитания, опираясь на представленные выше в учебнике иллюстрации.

6.1.10. (ПК-1-БЗ-5)

Какой прием используют учащиеся при решении примеров вида: 35+2, 35+20:

• Заменяют первое слагаемое суммой разрядных слагаемых и применяют правило прибавления числа к сумме;
• Заменяют первое слагаемое суммой удобных слагаемых и применяют правило прибавления числа к сумме;
• Используют прием округления.

6.1.11 (ПК-1-БЗ-6)

Назовите приемы устного и письменного сложения и вычитания в пределах тысячи.

6.1.12 (ПК-1-БЗ-6)

Приведите пример рассуждений ученика при выполнении сложения, когда в одном или двух разрядах значения суммы получается нуль?

6.1.13 (ПК-1-БЗ-7)

Приведите пример рассуждений ученика при выполнении вычитания, когда в одном разряде уменьшаемого нуль и требуется «занимать» десяток в соседнем разряде.

6.1.14 (ПК-1-БЗ-7)

Какие знания и умения необходимы при решении примеров вида: 30+20; 300+200; 50-30; 80+70; 500-300. Какие подготовительные упражнения предшествуют данному вычислительному приему?

6.1.15 (ПК-1-БЗ-8)

Назовите свойства (правила), которые лежат в основе приемов устного сложения двузначных чисел и приведите примеры.

6.1.16 (ПК-1-БЗ-8)

Придумайте задания для младших школьников, в процессе выполнения которых учащиеся будут рассматривать объекты с различных точек зрения.

6.1.17 (ПК-1-БЗ-9)

Подберите различные пары предметов и изображений (моделей) которые можно предложить первоклассникам, чтобы они установили сходство и различие между предметами. Придумайте иллюстрации к заданию «Что изменилось…?»

6.1.18 (ПК-1-БЗ-9)

Придумайте задания, при выполнении которых нужно использовать приём сравнения.

6.1.19 (ПК-1-БЗ-10)

Придумайте задания, при выполнении которых нужно использовать приём классификации по различным основаниям.

6.1.20 (ПК-1-БЗ-10)

ПОВЫШЕННЫЙ УРОВЕНЬ ПК-1 ПЗ

6.1.1. (ПК-1-ПЗ-1)

Придумайте ситуации для теоретического и эмпирического обобщения при изучении какого-либо математического понятия в начальной школе.

6.1.2. (ПК-1-ПЗ-2)

Найдите в учебниках математики для 1 класса разных авторов задания, которые можно использовать для формирования представлений о количественном и порядковом числе.

6.1.3. (ПК-1-ПЗ-2)

Найдите в учебниках математики для 1 класса разных авторов задания, которые можно использовать для формирования представлений о связи между количественным и порядковым числом.

6.1.4. (ПК-1-ПЗ-2)

Найдите в учебниках математики разных авторов задания, которые можно использовать для разъяснения принципа образования натурального ряда чисел. Придумайте свои задания.

6.1.5.(ПК-1-ПЗ-3)

6.1.6.(ПК-1-ПЗ-3)

Придумайте задания с использованием различных моделей, которые можно предложить младшим школьникам для усвоения действия сложения.

6.1.7.(ПК-1-ПЗ-4)

Придумайте задания с использованием различных моделей, которые можно предложить младшим школьникам для усвоения действия вычитания.

6.1.8.(ПК-1-ПЗ-4)

Придумайте задания с использованием различных моделей, которые можно предложить младшим школьникам для усвоения действия умножения.

6.1.9.(ПК-1-ПЗ-5)

Придумайте задания с использованием различных моделей, которые можно предложить младшим школьникам для усвоения действия деления.

6.1.10 (ПК-1-БЗ-5)

Составьте задания, в процессе которых у младших школьников формируются представления о длине и единицах её измерения.

6.1.11 (ПК-1-БЗ-6)

Составьте задания, в процессе которых у младших школьников формируются представления о массе и единицах её измерения.

6.1.12 (ПК-1-БЗ-6)

Составьте задания, в процессе которых у младших школьников формируются представления о площади и единицах её измерения.

6.1.13 (ПК-1-БЗ-7)

Составьте задания, в процессе которых у младших школьников формируются представления о времени и единицах его измерения,

6.1.14 (ПК-1-БЗ-7)

Составьте задания, в процессе которых у младших школьников формируются представления о объёме и единицах его измерения.

6.1.15(ПК-1-БЗ-8)

Найдите в учебниках математики разных авторов задания, которые можно предложены учащимся при изучении переместительного свойства сложения. Придумайте свои задания для изучения данных свойств арифметических действий.

6.1.16(ПК-1-БЗ-8)

Найдите в учебниках математики разных авторов задания, которые можно предложены учащимся при изучении переместительного свойства умножения. Придумайте свои задания для изучения данных свойств арифметических действий.

6.1.17(ПК-1-БЗ-9)

Найдите в учебниках математики разных авторов задания, которые можно предложены учащимся при изучении распределительного свойства умножения. Придумайте свои задания для изучения данных свойств арифметических действий.

6.1.18(ПК-1-БЗ-9)

Найдите в учебниках математики разных авторов задания, которые можно предложены учащимся при изучении свойства деления суммы на число. Придумайте свои задания для изучения данных свойств арифметических действий.

6.1.19(ПК-1-БЗ-10)

Подберите или составьте задания, в процессе выполнения которых учащиеся усваивают смысл деления с остатком, используйте приёмы сравнения, выбора, преобразования графических и математических моделей.

6.1.20. (ПК-1-БЗ-10)

Проанализируйте учебники математики (автор и класс – по выбору) и приведите примеры 3–4 учебных заданий, нацеленных на решение одной учебной задачи. Приведите примеры заданий, в процессе выполнения которых учащиеся решают несколько учебных задач.

ПОВЫШЕННЫЙ УРОВЕНЬ (ПК-1-ПЗ)

6.1.1. (ПК-1-ПЗ-1)

Составьте фрагмент конспекта урока, используя одно задание из учебника математики (автор и класс – по выбору). На выполнение какой учебной задачи оно будет направлено?

6.1.2. (ПК-1-ПЗ-1)

Проведите методический анализ урока (видео–урок, посещённый в школе) по следующим вопросам:

1) Какова тема (математическое содержание) и цель (методиче­ская задача) урока?

2) Соответствует ли логика построения урока его цели? (Име­ется в виду соответствие последовательности подобранных педа­гогом учебных заданий цели урока. Для ответа на этот вопрос пе­дагог, анализирующий урок, должен уметь адекватно определять цель каждого задания и их взаимосвязь.) При анализе заданий проводится также анализ их функций в организации познавательной деятельности детей: какие задания преобладали — тренировочные, репродуктивные, частично–поис­ковые или творческие?

3) Какова внутренняя структура урока: использована ли про­блемная ситуация, или урок построен на преимущественном ис­пользовании объяснительно–иллюстративного догматического метода? Какая деятельность детей преобладала — подражательная, воспроизводящая или поисковая (продуктивная)?

4) Грамотно ли педагог использовал математическую терминоло­гию, насколько чётко и логично ставил вопросы? Как реагировал на ответы детей? Какие приёмы организации помощи использовал?

5) Как урок спланирован и выдержан по времени? Целесооб­разно ли распределены виды деятельности детей, учтены ли тре­бования здоровьесбережения?

6) Как учтены индивидуальные особенности детей в классе? Как организована индивидуализация работы детей?

7) Какие формы и средства организации учебной деятельности использованы педагогом? (Как сочетаются фронтальные, группо­вые и индивидуальные формы? Какая наглядность, её эстетиче­ское оформление и её действенность при формировании понятий и способов действий?)

8) Удалось ли педагогу установить контакт со всеми детьми в классе (обратная связь)? Какими приёмами педагог осуществлял коррекцию их действий, создавал ситуацию успеха, реализовывал сотрудничество между детьми и педагога и детей?

9) Какие моменты урока показались особенно удачными? Не со­всем удачными?

10) Каков итог урока? Какие рекомендации можно дать педагогу по улучшению методики проведения уроков математики?

6.1.3. (ПК-1-ПЗ-2)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Сравнение чисел»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.4. (ПК-1-ПЗ-2)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Раскрытие смысла действий сложения»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.5. (ПК-1-ПЗ-3)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Раскрытие смысла действий вычитания»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.6. (ПК-1-ПЗ-3)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Раскрытие смысла действий умножения»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.7. (ПК-1-ПЗ-4)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Раскрытие смысла действий деления»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.8. (ПК-1-ПЗ-4)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Число и цифра 0»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.9. (ПК-1-ПЗ-5)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Открытие свойств арифметических действий»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.10. (ПК-1-ПЗ-5)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Приёмы устного умножения и деления»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.11. (ПК-1-ПЗ-6)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Деление с остатком»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.12. (ПК-1-ПЗ-6)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Знакомство с величиной «длина»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.13. (ПК-1-ПЗ-7)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Знакомство с величиной «площадь»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.14. (ПК-1-ПЗ-7)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Знакомство с величиной «время»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.15. (ПК-1-ПЗ-8)

Как можно организовать проблемную ситуацию для младших школьников по теме.

«Знакомство с величиной «масса»? Приведите примеры организации не менее 3-х проблемных ситуаций.

6.1.16. (ПК-1-ПЗ-8)

Составьте конспект урока математики, используя страницу учебника (автор учебника и класс – по выбору). Используйте следующую схему:

Учебник, класс________________________________________________

Тема урока____________________________________________________

Цель, задачи__________________________________________________

Этапы урока	Ход урока	Примечания

6.1.17.(ПК-1-ПЗ-9)

Разработайте игровые ситуации и занимательные упражнения, которые можно использовать при изучении арифметических действий с числами первого десятка.

6.1.18.(ПК-1-ПЗ-9)

Прежде чем приступить к обучению вычислительному приему а - 5 (6,7,8,9) учитель следующие актуализировал знания о связи между суммой и слагаемыми и умения решать примеры вида а + 5,6,7,8,9. Дайте характеристику правильности действий учителя.

6.1.19.(ПК-1-ПЗ-10)

Сделайте анализ предложенного фрагмента урока. Соответствуют ли предлагаемые на уроке задания задачам урока? Какие подходы используются для формирования знаний о числе? Какими методами формируется понятия о числе? Какие средства обучения используются? Какие еще задания может предложить учитель для закрепления знаний о числе и цифре 4? Какие изменения можно внести в ход урока?

Фрагмент урока

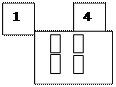
• Соотнести количество, число и цифру (рис.5). Расположить числа по порядку от меньшего к большему.

Рис.5

1) Поднимите нужные карточки. Какие числа меньше, чем 4. Какие числа больше, чем 1. Какое число меньше 4, но больше 2. Назови «соседей» числа 3.

2) Назовите число, которое меньше, чем 4 на 1. Назовите число, которое больше, чем 3 на 1.

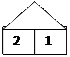
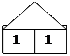
3) Найдите «дом» для числа 2, 3 и 4 (рис. 6). Объясните свой выбор.

Рис.6

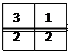4) На катке катались две девочки и один мальчик. Сколько детей катались на катке?

5) У Кати было 4 конфеты, 1 конфету она дала Тане. Сколько конфет осталось у Кати? Сколько конфет должна была Катя дать Тане, чтобы у девочек стало конфет поровну?

Актуализация знаний. Назовите числа от 1 до 4. Как получить число 2? (К 1 добавить 1). Как получить число 3? (К 2 добавить 1). Какое число получиться, если к 3 добавить 1?

Усвоение новых знаний. Сегодня мы к 4 добавим 1. Возьмем 4 красных круга и 1 синий круг. Пересчитаем все круги: один, два, три, четыре, пять. Всего пять кругов. Если к 4 добавить 1, получиться 5. Общее количество кругов 5. Число 5 записывается цифрой 5. Давайте определим, из каких чисел состоит число 5. На доске 5 кругов, из них 4 красных и 1 синий. Значит 5 это 4 и 1. Изменим количество красных и синих кругов. Синих возьмем больше, чем было – 2, а красных нужно взять меньше, чем было – 3. Общее количество кругов не измениться. Значить 5 состоит из 3 и 2.

Формирование умений. Найдите в кабинете 5 предметов. Возьмите 5 квадратиков и столько же треугольников. Уменьшите количество треугольников на 1. Сколько стало треугольников? Как получилось число 4? (От 5 отняли 1). Каких фигур стало больше? На сколько 5 больше, чем 4? Каких фигур стало меньше? На сколько 4 меньше, чем 5?

Работа по учебнику и в тетради. Конец фрагмента.

6.1.20. (ПК-1-ПЗ-10)

Сделайте анализ предложенного фрагмента урока «Изучение письменных приемов сложения и вычитания». Какие поставленные задачи были решены входе представленного фрагмента? Какие еще задания можно было бы предложить учащимся на этапе устного счета? Какими методами осуществляется объяснение нового материала? Какую наглядность необходимо использовать на данном уроке?

Фрагмент урока

Тема: Изучение письменных приемов сложения и вычитания.

Задачи: Повторить нумерацию чисел в пределах первой сотни; закрепить умение выполнять сложение и вычитание, основанное на знании нумерации, прибавлять к двузначному числу и вычитать из двузначного числа разрядные десятки, складывать и вычитать однозначные и двузначные числа без перехода и с переходом через разряд; познакомить с алгоритмами письменного сложения и вычитания чисел в пределах первой сотни; показать форму записи письменных приемов сложения и вычитания.

Устный счет:

6) Посчитайте десятками от 30 до 80, от 100 до 60.

7) Вставьте пропущенные числа: 74, 75, …, 77, 78, …, …, …, 82.

8) Охарактеризуйте число 49. Между какими числами стоит это число? Сколько в числе разрядных десятков и единиц? Какими цифрами записано число? Округлите число.

9) Назовите число, которое состоит из 6 десятков и 3 единиц.

10) Замените число 56 суммой разрядных слагаемых.

11) Найдите ошибку: 57+30=87; 46-2=26; 76+4=90; 62-5=57

12) В магазин привезли 100 штук яиц в коробке. Один покупатель купил 3 десятка яиц, другой на 2 десятка меньше, чем первый. Сколько яиц осталось для продажи?

Актуализация знаний. Решим пример: 32+45. Объясним ход его выполнения.

32+45=32+(40+5)=(32+40)+5=72+5=77 «К 32 прибавим 45. Второе слагаемое 45 состоит из 4 десятков и 5 единиц, прибавим к 32 сначала 40, потом еще 5, получим 77».

Решим пример 74-23.

74-23=74-(20+3)=74-20-3=54-3=51 «От 74 отнимем 23. Вычитаемое 23 состоит из 2 десятков и 3 единиц, отнимем от 74 сначала 20, потом еще 3, получим 51».

Усвоение новых знаний. Эти примеры вы решали устными приемами, так нужно считать в уме. Сегодня мы познакомимся с письменными приемами сложения и вычитания. Выполним еще раз сложение 32 и 45, но сделаем другую запись. Расположим слагаемые один под другим «в столбик». Обратите внимание, что единицы располагаются под единицами, а десятки под десятками. Слава между слагаемыми поставим знак плюс. Под вторым слагаемым проведем черту, они заменит знак равно. Начнем выполнять сложение с разряд единиц. К 2 единицами прибавим 5 единиц, будет 7 единиц. Под единицами запишем 7. Сложим десятки. К 3 десяткам прибавим 4 десятка, будет 7 десятков. Запишем под десятками 7. Какое число получилось в результате сложения? 77.

Вычитание выполняется аналогично. Решим еще раз пример 74-23, используя запись примера «в столбик». Как нужно записывать числа? Один под другим, разряд под разрядом. Запишем 74. Где запишем единицы числа 23 - цифру 3? Под цифрой 4. Где запишем число десятков вычитаемого – цифру 2? Под цифрой 7. Почему? Потому что цифра 7 показывает количество десятков в уменьшаемом, а нам нужно записать десятки под десятками. Где поставим знак минус? Слева от компонентов действий, между ними. Что обозначает черта под вычитаемым? Знак равно. С какого разряда начнем выполнять действие? С разряда единиц. От 4 единиц отнимем 3 единицы, получим 1. Запишем цифру 1 под единицами. Выполним действие с десятками. От 7 десятков отнимем 2 десятка, получим 5 десятков. Запишем цифру 5 под десятками. Какое число получилось в результате вычитания? 51.

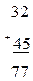
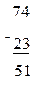
Формирование умений. Как выполняется запись примера, если мы будем при решении пользоваться письменными приемами сложения и вычитания? Что нужно записать под единицами первого компонента действия? Что нужно записать под десятками второго компонента действия? Где ставиться знак действия? Как записывается знак равно? С какого разряда нужно начинать выполнять действие? Что нужно прибавить к единицам первого слагаемого? Что нужно прибавить к десятками первого слагаемого? Что нужно отнять от единиц уменьшаемого? Что нужно отнять от десятков уменьшаемого? Где записывается результат действия с единицами? С десятками?

Прочитайте пример 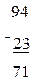. Назовите уменьшаемое. Сколько единиц в уменьшаемом? Сколько десятков в уменьшаемом? Назовите вычитаемое. Сколько единиц в вычитаемом? Сколько десятков в вычитаемом? Как расположены единицы уменьшаемого и вычитаемого? Как расположены десятки уменьшаемого и вычитаемого. Что означает цифры 1 в значении разности. Как получилась число 1 в значении разности? Что означает цифра 7 в значении разности? Как получилось число 7 в значении разности?

Работа по учебнику и в тетради. Конец фрагмента.

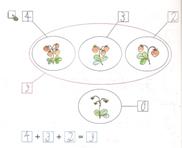
6.1.10. (ПК-1-ПЗ-5)

Составьте объяснение выполнения задания, представленного на рис. 15 из рабочей тетради для 1 класса М.М. Безруких, М.И. Кузнецовой, Е.Э. Кочуровой[1]. Какие методические приемы можно использовать?

Рис. 15

6.2. Задания, направленные на формирование профессиональных умений:

БАЗОВЫЙ УРОВЕНЬ ПК-1-БУ

6.2.1.(ПК-1-БУ-1)

Какие ошибки допустил ученик при выполнении заданий в рабочей тетради для 1 класса М.М. Безруких, М.И. Кузнецовой, Е.Э. Кочуровой[2] (рис. 16, рис. 17)? В рабочей тетради для 1 класса В.Н. Рудницкой[3] (рис. 18). В чем причина ошибок? Каковы приемы работы с учеником?

Рис. 16 Рис. 17.

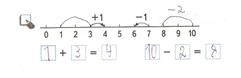
Рис. 18

6.2.2.(ПК-1-БУ-1)

Найдите в учебниках разных авторов задания, которые можно использовать для формирования табличных навыков сложения и соответствующих навыков вычитания в пределах 10, 20. Придумайте свои задания.

6.2.3.(ПК-1-БУ-2)

Найдите в учебниках разных авторов задания, которые можно использовать для формирования умения складывать и вычитать однозначные и двузначные числа без перехода в другой разряд.

6.2.4.(ПК-1-БУ-2)

Найдите в учебниках разных авторов задания, которые можно использовать для формирования умения складывать и вычитать однозначные и двузначные числа с переходом в другой разряд.

6.2.5.(ПК-1-БУ-3)

Проанализируйте приёмы изучения табличного умножения в учебниках разных авторов. Составьте несколько упражнений для формирования навыка табличного умножения и соответствующего навыка деления.

6.2.6.(ПК-1-БУ-3)

Воспроизведите алгоритм письменного сложения на примере задания: Вычисли значение суммы 123746 + 8502.

6.2. 7 . (ПК-1-БУ-4)

Воспроизведите алгоритм письменного вычитания на примере задания: Вычисли значение частного 37418 – 5579.

6.2. 8.(ПК-1-БУ-4)

Воспроизведите алгоритм письменного умножения на примере задания: Вычисли значение произведения 3215 · 740.

6.2. 9. (ПК-1-БУ-5)

Воспроизведите алгоритм письменного деления на примере задания: Вычисли значение частного 2712: 4.

6.2.10.(ПК-1-БУ-5)

Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного сложения.

6.2.11.(ПК-1-БУ-6)

Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного умножения.

6.2.12.(ПК-1-БУ-6)

Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного вычитания.

6.2.13.(ПК-1-БУ-7)

Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного деления.

6.2.14. (ПК-1-БУ-7)

Придумайте задания, которые можно предложить ученикам для усвоения названий геометрических фигур.

6.2.15. (ПК-1-БУ-8)

Придумайте задания, которые можно предложить ученикам для усвоения сравнения геометрических фигур.

6.2.16. (ПК-1-БУ-8)

Придумайте задания, которые можно предложить ученикам для определения существенных свойств геометрических фигур.

6.2.17. (ПК-1-БУ-9)

Приведите рассуждения учащихся при решении уравнений:

х – 12 = 34 150: х = 50 5 · х – 10 = 290.

6.2.18.(ПК-1-БУ-9)

Рассмотри стр. 12-13 учебника м