Правила действий со степенями
| формулы | примеры |
| 1 Умножение степеней с одинаковыми основаниями аn*am= an+m Чтобы перемножить степени с одинаковыми основаниями, надо основание степени оставить тем же, а показатели степеней сложить. | 25*2-3 = 25+(-3) = 22=4 a3,5*a-0,5 = a3,5-0,5 = a3 |
| 2. Деление степеней с одинаковыми основаниями аn:am= an-m Чтобы разделитьстепени с одинаковыми основаниями, надо основание степени оставить тем же, а показатели степеней вычесть. | 53:52 = 53-2 =5 х6:х-2=х6-(-2)=х8 |
| 3.Возведение степени в степень (an)m = anm Чтобы возвести степень в степень, надо показатели степеней перемножить. | (76)1/2 = 73 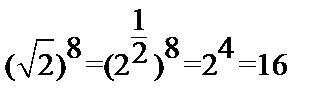 |
| 4. Возведение произведения в степень (ab)n = an*bn Чтобывозвести произведениевстепень,достаточновозвести встепенькаждый множитель. | (16*3)2 =162*32 =28*32 (аb-2)5=а5*(b-2)5=а5*b-10=  |
5.Возведение дроби в степень 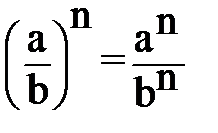 Чтобывозвести дробьв степень,достаточновозвести встепеньчислитель и знаменатель. Чтобывозвести дробьв степень,достаточновозвести встепеньчислитель и знаменатель. | 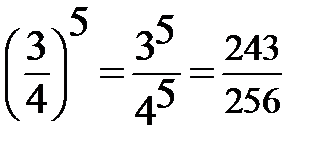 |
1.2.4.Примеры:
1) Вычислить: 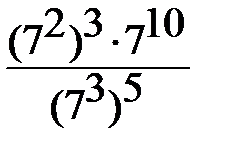 =
= 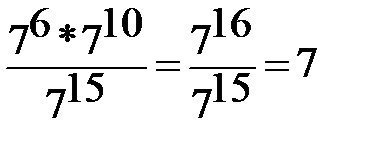
2)Выполнить возведение в степень: 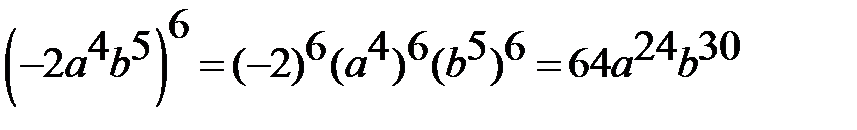
3) Известно, что: 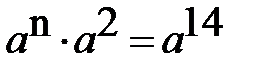 Чему равны n, p, x?
Чему равны n, p, x?
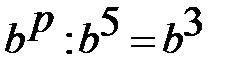
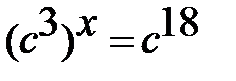
Решение
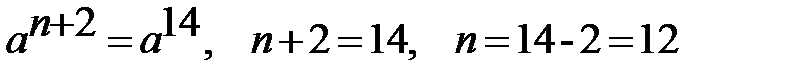
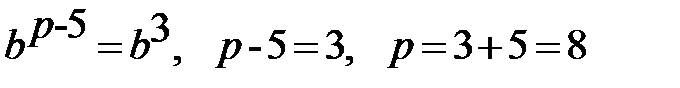
4) При каком х выполняется равенство:
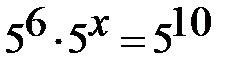 ,6+x=10, х=10-6=4
,6+x=10, х=10-6=4
5) 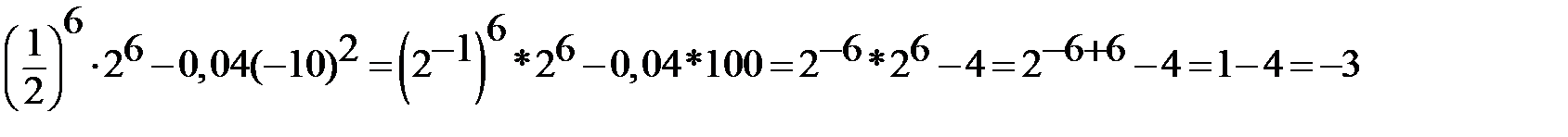
6. 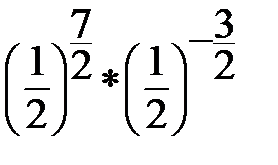 = = 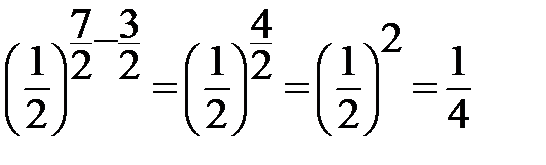 |
7. 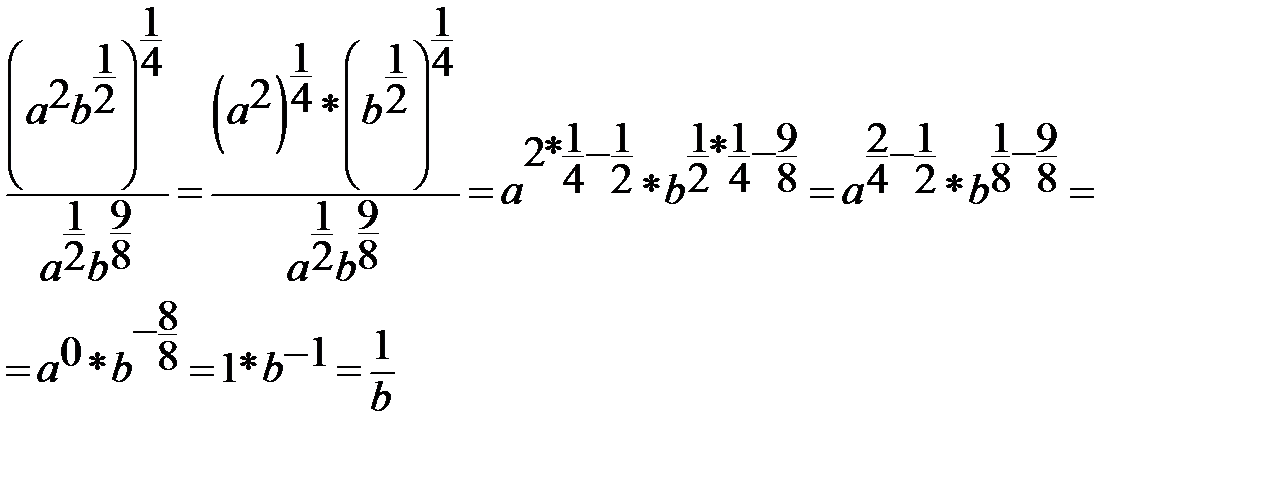 |
8. 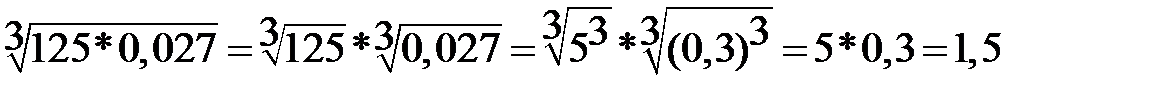 |
9. 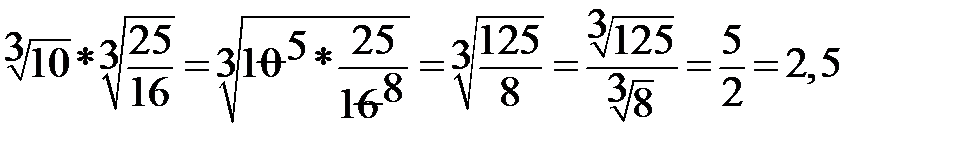 10. 10. 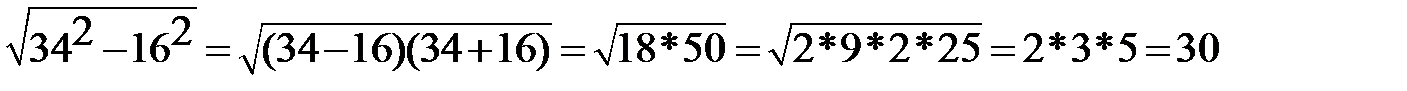 11. 11. 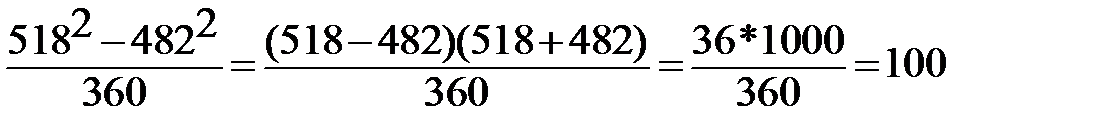 |
Потренируйтесь!
| Задание | Выберите правильный ответ |
1) Вычислить: 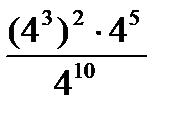 | а) 16; б) 4; в) 8; г) 12 |
2)Выполнить возведение в степень: 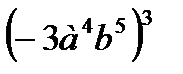 | а) 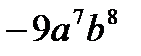 ; б) ; б) 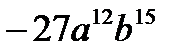 ; ; |
3)Известно, что 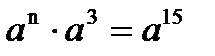 ; ; 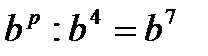 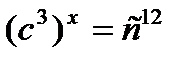 Чему равны n, p, x? Чему равны n, p, x? | а) n=18; p=9; x=5; б) n=4; p=2; x=7; в) n=15; p=9; x=4; г) n=12; p=11; x=4. |
4)При каком х выполняется равенство 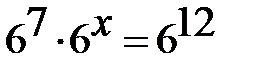 | а) 36; б) 10; в) 5; г) 4 |
Продолжите предложения:
1)При умножении степеней с одинаковым основанием ...
2)При делении степеней с одинаковым основанием...
3) При возведении степени в степень…
4) При возведении произведения в степень ...
5) При возведении дроби в степень…
6)действие, с помощью которого вычисляется значение степени, ...
7)Произведение, состоящее из одинаковых множителей, — ....
8)Действие с показателями при возведении степени в степень — ...
9)Действие со степенями, при которых показатели степеней вычитаются, — ...
10) Число всех одинаковых множителей —…
11) Степень с нулевым показателем — …
12) Повторяющийся множитель — ...
13) Значение выражения: 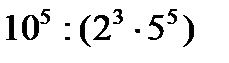 …
…
14) Показатель степени, который обычно не пишут-…
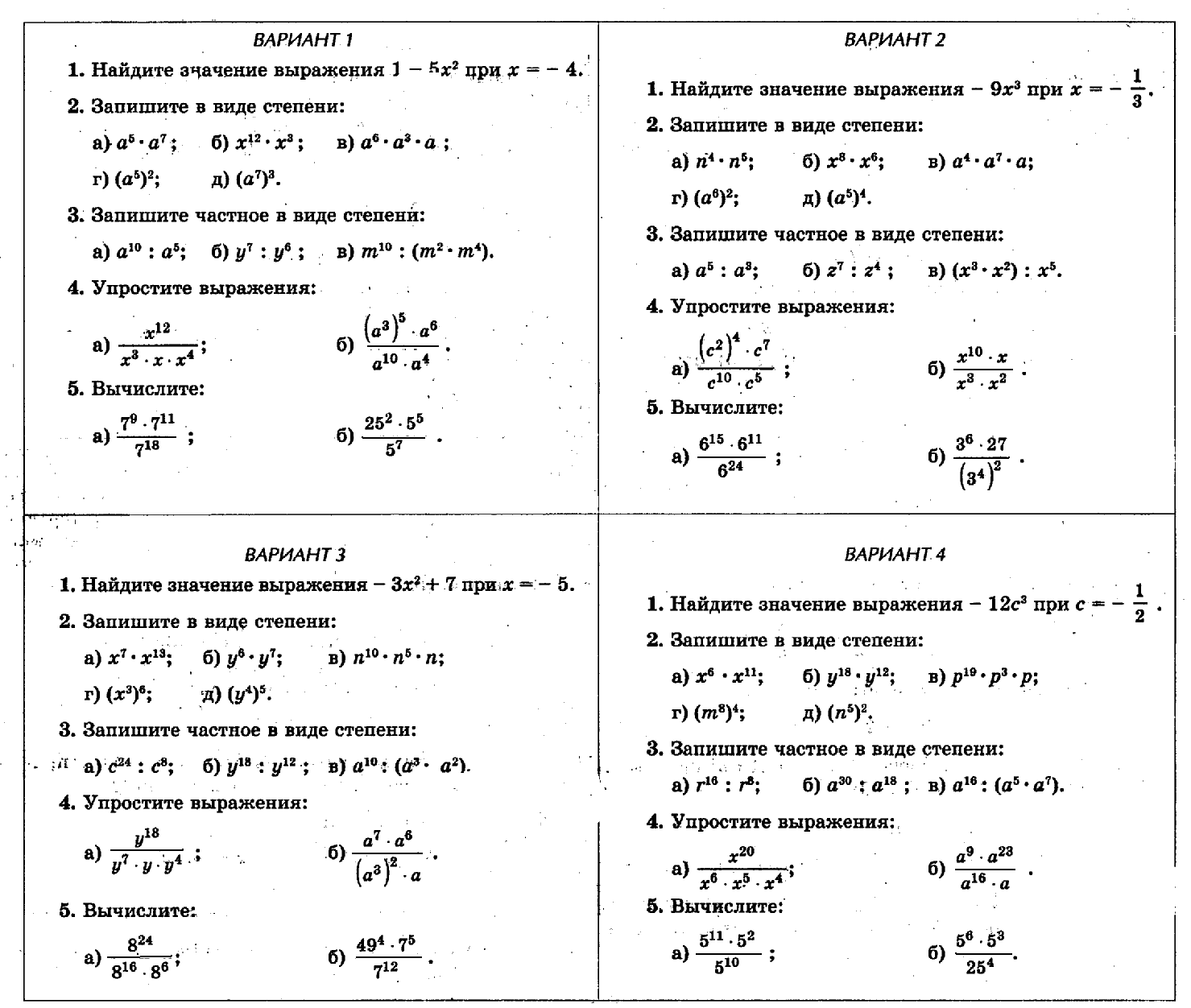
Ответы:
Вариант 1 Вариант 2 Вариант 3 Вариант 4
1)-79 1)  1) -68 1) 1,5
1) -68 1) 1,5
2) а) 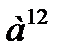 2) а)
2) а) 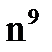 2) а)
2) а) 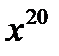 2) а)
2) а) 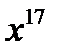
б) 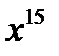 б)
б) 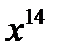 б)
б) 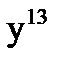 б)
б) 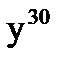
в) 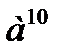 в)
в) 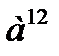 в)
в) 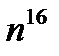 в)
в) 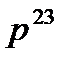
г) 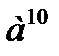 г)
г) 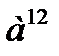 г)
г) 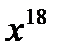 г)
г) 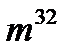
д) 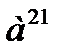 д)
д) 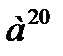 д)
д) 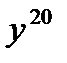 д)
д) 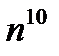
3) а) 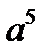 3) а)
3) а) 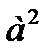 3) а)
3) а) 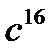 3) а)
3) а) 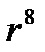
б)y б) 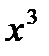 б)
б) 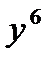 б)
б) 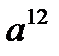
в) 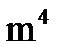 в)1в)
в)1в) 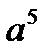 в)
в) 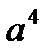
4) а) 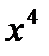 4) а)1 4) а)
4) а)1 4) а) 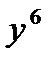 4) а)
4) а) 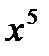
б) 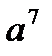 б)
б) 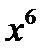 б)
б) 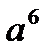 б)
б) 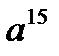
5) а)49 5) а) 36 5) а)645) а)125
б)25 б) 3 б)7б)5
Исправьте ошибку
а) 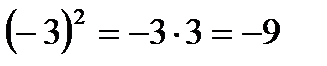 г)
г) 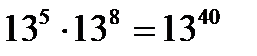 ж)
ж) 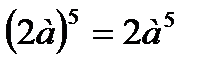
б) 
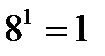 д)
д) 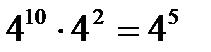 з)
з) 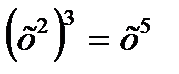
в) 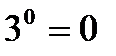 е)
е) 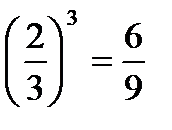 и)
и) 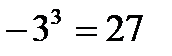
1.2.5. Индивидуальные задания-ИЗ-2
(Номер вариант равен остатку от деления номера по списку на 4)
| 1 вариант | 2 вариант | 3 вариант | 4вариант | |
1. 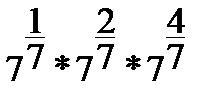 | 1. 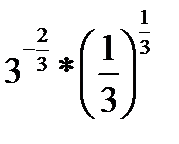 . . | 1. 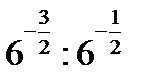 | 1. 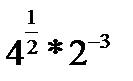 | |
2. 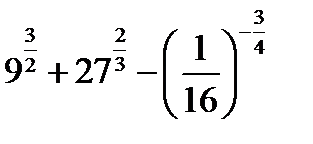 | 2. 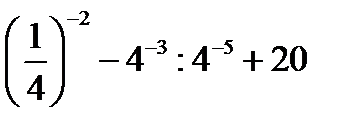  | 2. 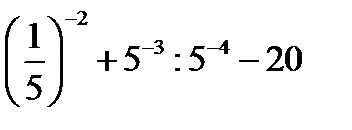 | 2. 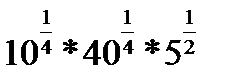 | |
3. 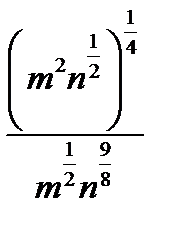 | 3. 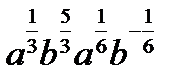 | 3. 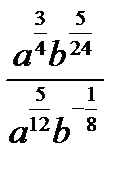 | 3.  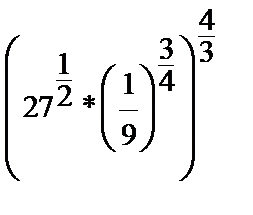 | |
4. 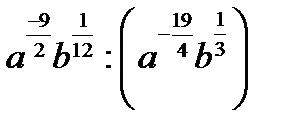 | 4. 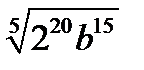 | 4. 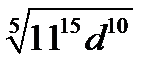 | 4. 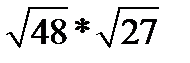 | |
5. 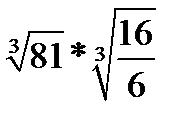 | 5. 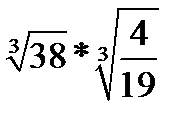 | 5. 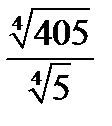 | 5. 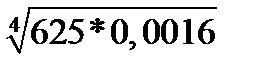 | |
Из материалов ЕГЭ
Найдите значение выражения:
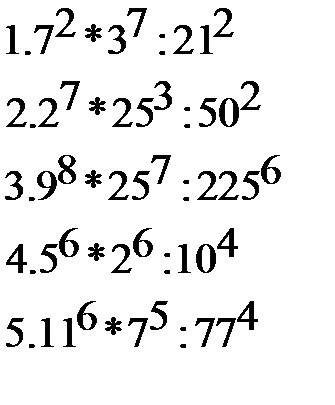 | 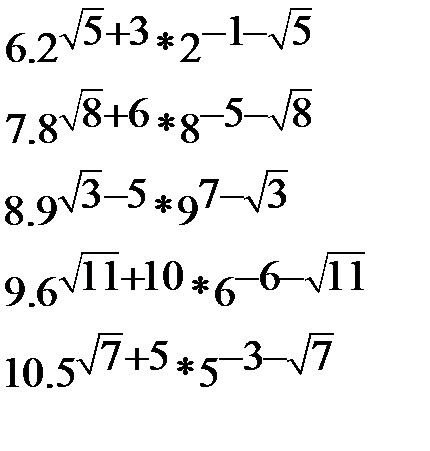 | 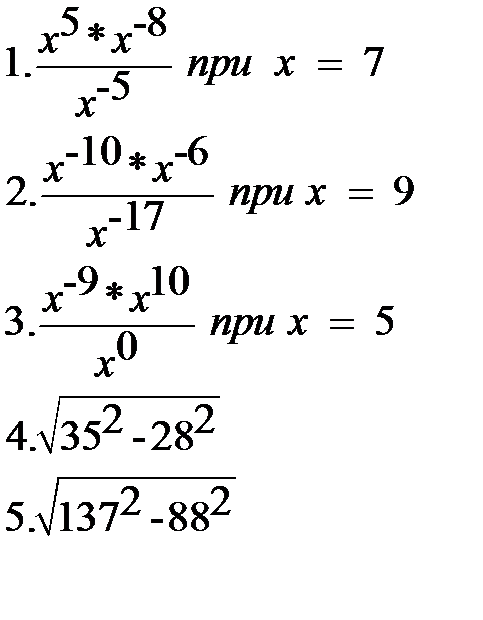 |
1.3.Тождественные преобразования алгебраических выражений
 | Франсуа Виет – юрист по образованию и математик по призванию, положивший начало алгебре как науке о преобразовании выражений, решению уравнений в общем виде, создатель буквенного исчисления |
Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в степень и извлечения корней и с помощью скобок составляются алгебраические выражения.
Примеры алгебраических выражений:
1)2а2b-3ab2(a+b); 2)a+b+ 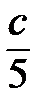 ; 3)
; 3) 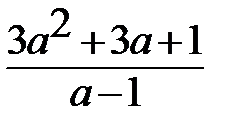 ; 4)
; 4) 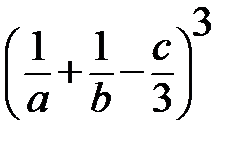 ; 5)
; 5) 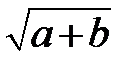
6) 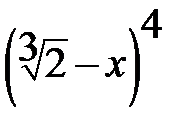 ; 7)
; 7) 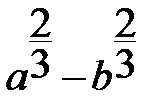
Если алгебраическое выражение не содержит деления на переменные и извлечения корня, то оно называется целым (1,2,6), в противном случае – дробным (3 и4). Если используется извлечение корня или возведение в дробную степень, то такое выражение называется иррациональным (5 и 7).
Целые и дробные – рациональные.
Преобразования выражений, не только алгебраических, нам придется в дальнейшем очень часто, поэтому важно научиться делать это хорошо.
В математике приняты следующие термины:
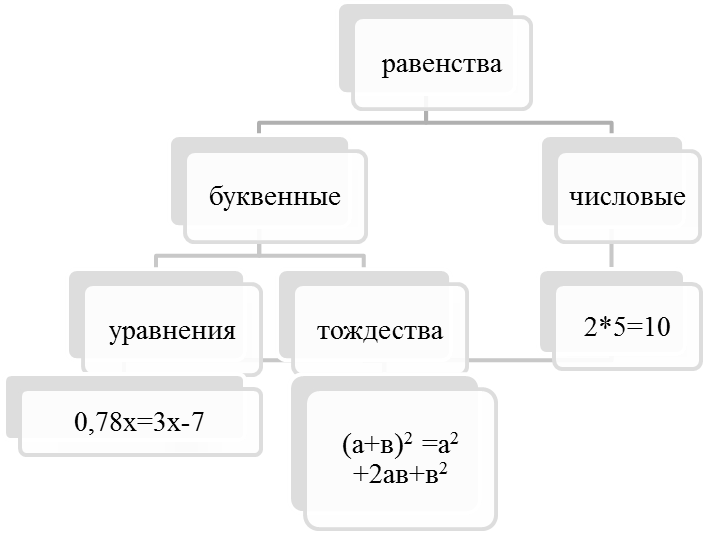
Уравнения – это равенства, которые выполняются только при некоторых значения переменных.
Тождества – это равенства, которые выполняются при всех значениях переменных.
Мы будем выполнять только тождественные преобразования, т.е. такие, при которых не изменяется значение выражения, меняется только внешний вид. Например, тождественно равны выражения: х5 и х2*х3, а+в+с и с+а+в, (2ав)2 и 4а2в2.
Примеры тождеств:
а+в=в+а, а+0=а, (а+в)*с=ас+вс, а*1=а.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения.
Основные понятия:
· Одночленом называется такое выражение, которое содержит числа, степени переменных и их произведения и не содержит никаких других действий над числами и переменными.
3а*(2,5а3), (5аb2)*(0,4c3d), x2y*(-2z)*0,75 – одночлены!!!
а+в, 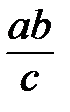 - НЕ одночлены!!! Числовой множитель – КОЭФФИЦИЕНТ.
- НЕ одночлены!!! Числовой множитель – КОЭФФИЦИЕНТ.
· Одночлены называются подобными, если они отличаются коэффициентами или не отличаются.
Например: 18х2уz3 и -8х2уz3, 3ав и 3ав – подобны.
Чтобы выполнить действия с одночленами, достаточно выполнить действия с коэффициентами. Это действие называется приведение подобных слагаемых.
· Многочлен – это сумма одночленов.
1.3.1.Основные тождественные преобразования
· Вынесение общего множителя за скобку
28х3-35х4= 7х3*4-7х3*5х=7х3(4-5х)
(Вынесение за скобку общего множителя предполагает выполнение действия деления: 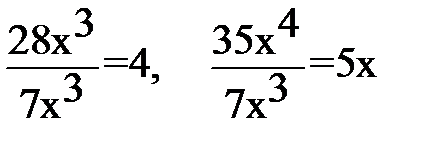 )
)
· Способ группировки
х3-3х2+5х-15=(х3-3х2)+( 5х-15)=х2(х-3)+5(х-3)=(х-3)(х2+5)
· Использование формул сокращенного умножения
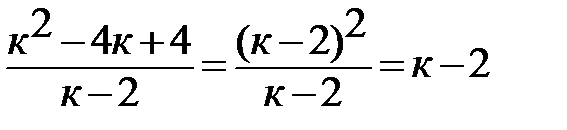
· Разложение на множители квадратного трехчлена.
4х2-5х+1=
4х2-5х+1=0,D=25-16=9>0, x1,2= 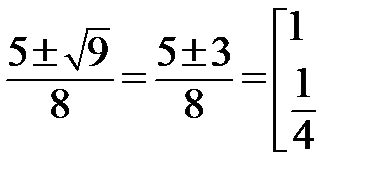
=4(x-1)(x-0,25)
