Интерпретация коэффициентов уравнения регрессии.

Коэффициент 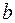при факторной переменной имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина при изменении фактора на 1 единицу измерения.

Коэффициент 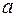– свободный член в уравнении регрессии показывает значения переменной при 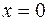. Этот коэффициент не всегда имеет экономическую интерпретацию.

Оценка тесноты связи.

В качестве меры для тесноты линейной связи между переменными используется коэффициент корреляции. Приведем формулу выборочного коэффициента корреляции переменных и :

.

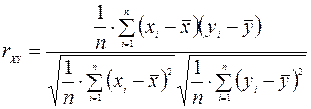Коэффициент корреляции будет положителен, если отклонения переменных и от своих средних значений, как правило, имеют одинаковый знак, и отрицательным – если разные знаки. Коэффициент корреляции является безразмерной величиной. Его величина меняется от -1 в случае строгой линейной отрицательной связи до +1 в случае строгой линейной положительной связи. Близкая к 0 величина коэффициента корреляции говорит об отсутствии линейной связи между переменными, но не об отсутствии связи между ними вообще.

Оценка качества построенной модели (адекватности эмпирическим данным).

2.6.1 Коэффициент детерминации. Для оценки качества построенной модели регрессии можно использовать коэффициент детерминации 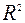. Коэффициент детерминации может быть вычислен по формуле:

.

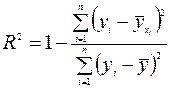С другой стороны, для парной линейной регрессии верно равенство:

.

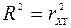При близости значения коэффициента детерминации к 1 говорят, что уравнение регрессии статистически значимо и фактор оказывает сильное воздействие на результирующий признак .

При анализе модели парной линейной регрессии по значению коэффициента детерминации можно сделать следующие предварительные выводы о качестве модели:

¾ Если 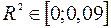, то будем считать, что использование регрессионной модели для аппроксимации зависимости между переменными и статистически необоснованно.

¾ Если 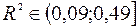, то использование регрессионной модели возможно, но после оценивания параметров модель подлежит дальнейшему многостороннему статистическому анализу.

¾ Если 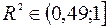, то будем. считать, что у нас есть основания для использования регрессионной модели при анализе поведения переменной .

Средняя ошибка аппроксимации.

Другой показатель качества построенной модели –– среднее относительное отклонение расчетных значений от фактических или средняя ошибка аппроксимации:

.

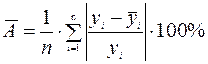Построенное уравнение регрессии считается удовлетворительным, если значение 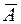не превышает 10% – 12% .

Пример.

По 21 региону страны изучается зависимость розничной продажи телевизоров ( ) от среднедушевого денежного дохода в месяц ( ).

Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	Объем розничной продажи телевизоров, тыс. шт.,
	2,4	21,3
	2,1
	2,6	23,3
	1,7	15,8
	2,5	21,9
	2,4
	2,6
	2,8	23,9
	2,6
	2,6	24,6
	2,5
	2,9
	2,6
	2,2
	2,6
	3,3	31,9
	3,9
		35,4
	3,7
	3,4

Необходимо найти зависимость, наилучшим образом отражающую связь между переменными и .

Рассмотрим вопрос применения модели линейной регрессии в этой задаче.

Построим поле корреляции, т.е. нанесем исходные данные на координатную плоскость. Для этого воспользуемся, например, возможностями MS Excel 2003.

Подготовим таблицу исходных данных.

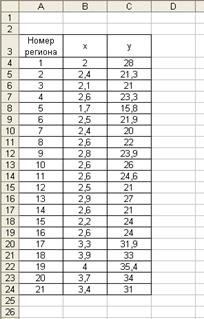
Нанесем на координатную плоскость исходные данные:

Характер расположения точек на графике дает нам основание предположить, что искомая функция регрессии линейная: 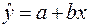. Для оценки коэффициентов уравнения регрессии необходимо составить и решить систему нормальных уравнений ( ).

По исходным данным рассчитываем необходимые суммы:

Номер региона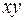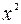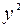
	2,4	21,3	51,12	5,76	453,69
	2,1		44,1	4,41
	2,6	23,3	60,58	6,76	542,89
	1,7	15,8	26,86	2,89	249,64
	2,5	21,9	54,75	6,25	479,61
	2,4			5,76
	2,6		57,2	6,76
	2,8	23,9	66,92	7,84	571,21
	2,6		67,6	6,76
	2,6	24,6	63,96	6,76	605,16
	2,5		52,5	6,25
	2,9		78,3	8,41
	2,6		54,6	6,76
	2,2		52,8	4,84
	2,6		62,4	6,76
	3,3	31,9	105,27	10,89	1017,61
	3,9		128,7	15,21
		35,4	141,6		1253,16
	3,7		125,8	13,69
	3,4		105,4	11,56
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему уравнений:

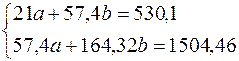
Имеем систему линейных алгебраических уравнений, которая может быть решена, например, по формулам Крамера. Для этого вычислим следующие определители:

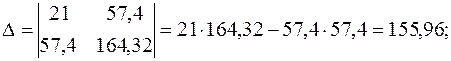
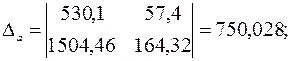
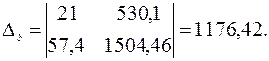
Тогда, согласно теореме Крамера,

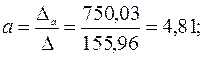
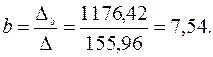
Получаем уравнение регрессии:

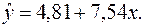
Величина коэффициента регрессии 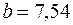означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент 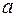в данном случае не имеет содержательной интерпретации.

Оценим тесноту линейной связи между переменными и качество построенной модели в целом.

Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.

Прежде всего, найдем выборочное среднее 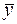по формуле:

.

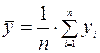Для рассматриваемого примера имеем:

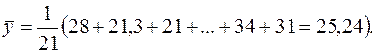
Теперь произведем расчет остальных вспомогательных величин:

Номер региона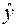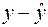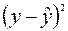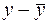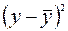
			19,76	8,24	67,89	2,76	7,60
	2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
	2,1		20,51	0,49	0,24	-4,24	18,00
	2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
	1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
	2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
	2,4		22,75	-2,75	7,57	-5,24	27,49
	2,6		24,25	-2,25	5,04	-3,24	10,52
	2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
	2,6		24,25	1,75	3,08	0,76	0,57
	2,6	24,6	24,25	0,35	0,13	-0,64	0,41
	2,5		23,50	-2,50	6,24	-4,24	18,00
	2,9		26,49	0,51	0,26	1,76	3,09
	2,6		24,25	-3,25	10,54	-4,24	18,00
	2,2		21,26	2,74	7,53	-1,24	1,54
	2,6		24,25	-0,25	0,06	-1,24	1,54
	3,3	31,9	29,48	2,42	5,86	6,66	44,32
	3,9		33,96	-0,96	0,93	7,76	60,17
		35,4	34,71	0,69	0,47	10,16	103,17
	3,7		32,47	1,53	2,34	8,76	76,69
	3,4		30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1			130,68		545,73

Здесь столбец « 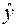» – это значения 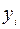, 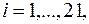рассчитанные с помощью построенного уравнения регрессии, столбцы « 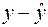» и 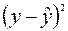– это столбцы, так называемых, «остатков»: разностей между исходными значениями 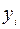, 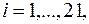и рассчитанными с помощью уравнения регрессии 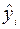, а также их квадратов, а в последних двух столбцах – разности между исходными значениями 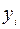, выборочным средним 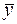, а также их квадраты.

Для вычисления коэффициента детерминации воспользуемся формулой ( ):

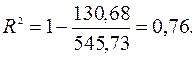
Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку .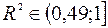

Построим линию регрессии на корреляционном поле, для чего добавим на координатной плоскости точки, соответствующие уравнению регрессии ( ).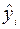

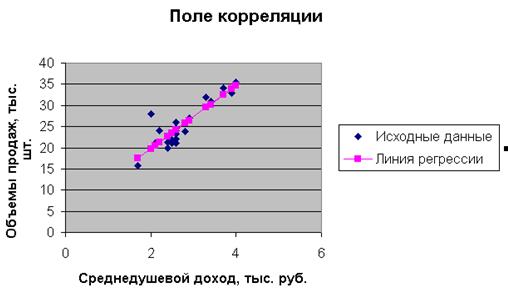
Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel. Для этого необходимо выделить правой кнопкой мыши исходные точки и выбрать опцию Добавить линию тренда.

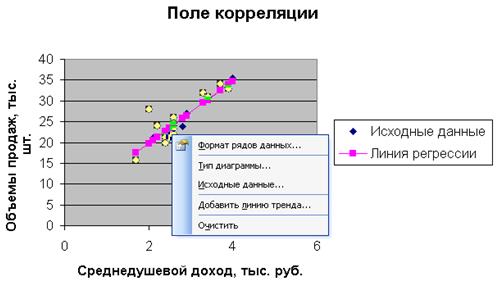
В открывшемся меню Параметры линии тренда выбрать Линейную аппроксимацию. Далее поставить флажок напротив полей Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации .

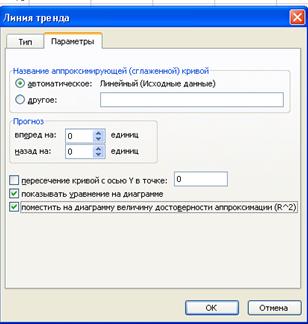
Нажав на ОК, получаем еще одну прямую на диаграмме, которая совпадает с построенными ранее точками линии регрессии:

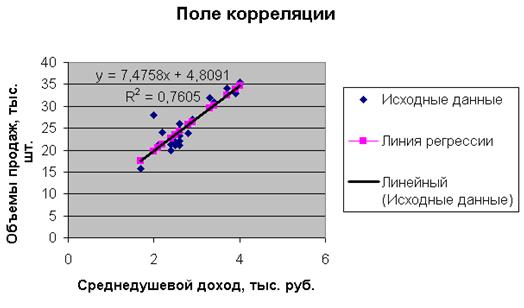
Сплошная черная линия на диаграмме – это линия регрессии, рассчитанная средствами Excel. Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.

Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:

Номер региона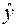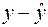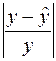
			19,76	8,24	0,29
	2,4	21,3	22,75	-1,45	0,07
	2,1		20,51	0,49	0,02
	2,6	23,3	24,25	-0,95	0,04
	1,7	15,8	17,52	-1,72	0,11
	2,5	21,9	23,50	-1,60	0,07
	2,4		22,75	-2,75	0,14
	2,6		24,25	-2,25	0,10
	2,8	23,9	25,74	-1,84	0,08
	2,6		24,25	1,75	0,07
	2,6	24,6	24,25	0,35	0,01
	2,5		23,50	-2,50	0,12
	2,9		26,49	0,51	0,02
	2,6		24,25	-3,25	0,15
	2,2		21,26	2,74	0,11
	2,6		24,25	-0,25	0,01
	3,3	31,9	29,48	2,42	0,08
	3,9		33,96	-0,97	0,03
		35,4	34,71	0,69	0,02
	3,7		32,47	1,53	0,05
	3,4		30,23	0,77	0,02

Здесь столбец « 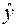» – это значения 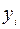, 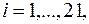рассчитанные с помощью построенного уравнения регрессии, столбец « 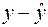» – это столбец так называемых «остатков»: разностей между исходными значениями 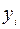, и рассчитанными с помощью уравнения регрессии 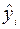, 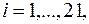и, наконец, последний столбец « 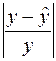» – это вспомогательный столбец для вычисления элементов суммы по формуле ( ). Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:

.

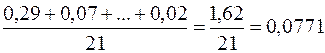Переведем это число в проценты и запишем окончательное выражение для средней ошибки аппроксимации:

.

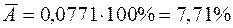Итак, средняя ошибка аппроксимации оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа. Предположим, что среднедушевой месячный доход в одном из регионов составит 4,1 тыс. руб. Оценим, каков будет уровень продаж телевизоров в этом регионе согласно построенной модели? Для этого необходимо выбранное значение фактора подставить в уравнение регрессии ( ):

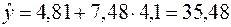(тыс. руб.),

т.е. при таком уровне дохода, розничная продажа телевизоров составит, в среднем, 35 480 телевизоров.