Маршруты, циклы в неориентированном графе
Пусть G - неориентированный граф. Маршрутомили цепью в G называется такая последовательность (конечная или бесконечная) вершин и ребер v0, x1, v1, x2, v2,... ,vn-1, xn, vn,..., что каждые соседние два ребра xi и xi+1имеют общую инцидентную вершину vi. Одно и то же ребро и/или вершина могут встречаться в маршруте несколько раз. Маршрут полностью задается последовательностью ребер (x1, x2,..., xn,...) или последовательностью вершин (v0, v1, v2,.. vn,..). В конечном маршруте (x1,x2,...xn) имеется первое ребро x1и последнее ребро xn. Вершина v0, инцидентная ребру x1, но не инцидентная ребру x2, называется началом маршрута, а вершина vn, инцидентная ребру xn, но не инцидентная ребру xn-1, называется концом маршрута.
Длиной(или мощностью) маршрута называется число ребер, входящих в маршрут, причем каждое ребро считается столько раз, сколько оно входит в данный маршрут.
Пример 4.6. В изображенном на рис. 4.3 графе рассмотрим два маршрута из вершины v1в вершину v4: M1= (x1, x4, x6) и M2= (x1, x3, x5, x6). Длина маршрута M1 равна 3, а длина маршрута M2 равна 4
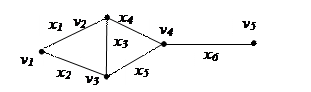
Рис.4.3
Замкнутый маршрут называется циклом.
Маршрут (цикл), в которой все ребра различны, называется простой цепью (циклом). Маршрут (цикл), в которой все вершины, (кроме первой и последней), различны, называется элементарной цепью (циклом). Гамильтонова цепь (цикл) − простая цепь (цикл), проходящая через все вершины. Эйлерова цепь (цикл) − цепь (цикл), содержащая все ребра графа по одному разу.
Пример 4.7. В приведенном на рис 4.3 графе выделим следующие маршруты:
(x1,x4,x6) – простая элементарная цепь длины 3, т.к. все ребра и вершины попарно различны;
(x1,x3,x2) – простой элементарный цикл, т.к. это замкнутый маршрут, у которого все ребра и вершины, кроме первой и последней, различны;
(x1,x3,x5,x4)– цепь, которая является простой, но не элементарной;
(x1,x3,x3) – цепь длины 3, не являющаяся ни простой, ни элементарной цепью, т.к. ребро x3и вершина v2 встречаются дважды;
(x1,x3,x5,x6) – Гамильтонова цепь.
Пути, контуры в ориентированном графе
Понятия пути, контура в ориентированном графе аналогичны понятиям цепи, цикла в неориентированном графе.
Путем ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги. Число дуг пути называетсядлиной пути.
Путь называется контуром, если его начальная вершина совпадает с конечной вершиной.
Путь (контур), в котором все дуги различны, называетсяпростым. Путь (контур), в котором все вершины, кроме первой и последней, различны, называетсяэлементарным. Гамильтонов путь (контур) − простой путь (контур), проходящий через все вершины. Эйлеров путь (контур) − путь (контур), содержащий все дуги графа по одному разу. Путь из vi в vj называется кратчайшим, если он содержит наименьшее число дуг по сравнению со всеми другими путями из vi в vj.
Отметим, что понятиям ребра, маршрута, цепи, цикла в неориентированном графе соответствуют понятия дуги, пути, ориентированной цепи, контура в ориентированном графе.
Пример 4.8. В приведенном на рис 4.4 орграфе выделим следующие пути:
(v1,v2,v3,v4) – простой элементарный путь, т.к. каждая вершина и каждая дуга используются не более одного раза;
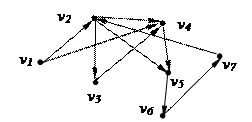
Рис. 4.4
(v2,v5,v6,v7,v2) – простой элементарный контур, т.к. это замкнутый путь, в котором все дуги и вершины, кроме первой и последней, различны;
(v1, v2,v3,v4,v5,v6) – Гамильтонов путь.
