Ix. Something about euclidean and non-euclidean geometries

1. It is interesting to note that the existence of the special quad­rilaterals discussed above is based upon the so-called parallel po­stulate of Euclidean geometry. 2. This postulate is now usually sta­ted as follows: Through a point not on line L, there is no more than one line parallel to L. 3. Without assuming (не допуская) that there exists at least one parallel to a given line through a point not on the given line, we could not state the definition of the special quadri­laterals which have given pairs of parallel sides. 4. Without the as­sumption that there exists no more than one parallel to a given line through a point not on the given line, we could not deduce the conclusion we have stated (сформулировали) for the special quadrila­terals. 5. An important aspect of geometry (or any other area of ma­thematics) as a deductive system is that the conclusions which may be drawn are consequences (следствие) of the assumptions which have been made. 6. The assumptions made for the geometry we have been considering so far are essentially those made by Euclid in Elements. 7. In the nineteenth century, the famous mathematicians Lobachevsky, Bolyai and Riemann developed non-Euclidean geomet­ries. 8. As already stated, Euclid assumed that through a given point not on a given line there is no more than one parallel to the given line. 9. We know of Lobachevsky and Bolyai having assumed inde­pendently of (не зависимо от) one another that through a given point not on a given line there is more than one line parallel to the given line. 10. Riemann assumed that through a given point not on a given line there is no line parallel to the given line. 11. These variations of the parallel postulate have led (npивели) to the creation (coздание) of non-Euclidean geometries which are as internally consistent (непротиворечивы) as Euclidean geometry. 12. However, the conclusions drawn in non-Euclidean geometries are often comple­tely inconsistent with Euclidean conclusions. 13. For example, accor­ding to Euclidean geometry parallelograms and rectangles (in the sense (смысл) of a parallelogram with four 90-degree angles) exist; according to the geometries of Lobachevsky and Bolyai parallelo­grams exist but rectangles do not; according to the geometry of Rie­mann neither parallelograms nor rectangles exist. 14. It should be borne in mind that the conclusions of non-Euclidean geometry are just as valid as those of Euclidean geometry, even though the conclusions of non-Euclidean geometry contradict (npoтиворечат) those of Euclidean geometry. 15. This paradoxical situation becomes intuitively clear when one realizes that any de­ductive system begins with undefined terms. 16. Although the mathematician forms intuitive images (o6paзы) of the concepts to which the undefined terms refer, these images are not logical neces­sities (необходимость). 17. That is, the reason for forming these in­tuitive images is only to help our reasoning (paccyждениe) within a certain deductive system. 18. They are not logically a part of the deductive system. 19. Thus, the intuitive images corresponding to the undefined terms straight line and plane are not the same for Eucli­dean and non-Euclidean geometries. 20. For example, the plane of Euclid is a flat surface; the plane of Lobachevsky is a saddle-shaped (седлообразный) or pseudo-spherical surface; the plane of Riemann is an ellipsoidal or spherical surface.

X. CIRCLES

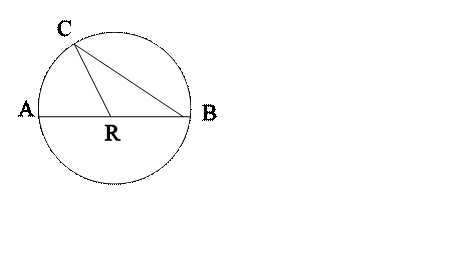
1. If you hold the sharp end of a compass fixed on a sheet of pa­per and then turn the compass completely around you will draw a curved line enclosing parts of a plane. 2. It is a circle. 3. Acircle is a set of points in a plane each of which is equidistant, that is the same distance from some given point in the plane called the cen­ter. 4. A line segment joining any point of the circle with the center is called a radius. 5. In the figure above R is the center and RC is the radius. 6. What other radii are shown? 7. A chord bf a circle is a line segment who­se endpoints are points on the circle. 8. A diameter is a chord which passes through the center of the circle. 9. In the figure above AB and BC are chords and AB is a diameter. 10. Any part of a circle containing more than one point forms an arc of the circle. 11. In the above figure, the points C and A and all the points in the inte­rior of ÐARC that are also points of the circle are called arc

Ç Ç

AC which is symbolized as AC. 12. ABC is the arc containing points A and C and all the points of the circle which are in the exterior of ÐABC. 13. Instead of speaking of the perimeter of a circle, we usually use the term circumference to mean the distance around the circle. 14. We cannot find the circumference of a circle by adding the measure of the segments, because a circle does not contain any seg­ments. 15. No matter how short an arc is, it is curved at least slightly. 16. Fortunately mathematicians have discovered that the ratio of the circumference (C) to a diameter (d) is the same for all

C

circles. This ratio is expressed d 17. Since d = 2r (the length of a diameter is equal to twice the length of a radius of the same circle), the follo­wing denote the same ratio.

CC

d= 2r since d=2r

C C

18. The number d or 2r which is the same for all circles, is designated by π 19. This allows us to state the following:
C C

d = π or 2r = π

20. By using the multiplication property of equation, we obtain the following:

C = πd or C = 2 πr.

XI. THE SOLIDS

A solid is a three-dimensional figure, e.g. a prism or a cone.

A prism is a solid figure formed from two congruent polygons with their corresponding sides parallel (the bases) and the parallelogram (lateral faces) formed by joining the corresponding vertices of the polygons. The lines joining the vertices of the polygons are lateral edges. Prisms are named according to the base - for example, a triangular prism has two triangular bases (and three lateral faces); a quadrangular prism has bases that are quadrilaterals. Pen­tagonal, hexagonal, etc. prism have bases that are pentagons, hexagons, etc.

A right prism is one in which the lateral edges are at right angles to the bases (i.e. the lateral faces are rectangles) - otherwise the prism is an oblique prism (i.e. one base is displaced with respect to the other, but remains parallel to it). If the bases are regular polygons and the prism is also a right prism, then it is a regular prism.

A cone is a solid figure formed by a closed plane curve on a plane (the base) and all the lines joining points of the base to a fixed point (the vertex) not in the plane of the base. The closed curve is the directrix of the cone and the lines to the vertex are its generators(or elements).The curved area of the cone forms its lateral surface.Cones are named according to the base, e.g. a circularcone or an ellipticalcone. If the base has a center of symmetry, a line from the vertex to the center is the axis of the cone. A cone that has its axis perpendicular to its base is a right cone; otherwise the cone is a oblique cone. The altitudeof a cone (h) is the perpendicular distance from the plane of the base to the vertex. The volumeof any cone is l/3hA,where A is the area of the base. A right circular cone (circular base with perpendicular axis) has a slant height(s), equal to the distance from the edge of the base to the vertex (the length of a generator). The term "cone" is often used loosely for "conical sur­face".

A pyramidis a solid figure (a polyhedron) formed by a polygon (the base) and a number of triangles (lateral faces) with a common vertex that is not coplanarwith the base. Line segments from the common vertex to the vertices of the base are lateral edges of the pyramid. Pyramids are named according to the base: a triangular pyramid (which is a tetrahedron), a square pyramid, a pentagonal pyramid, etc.

If the base has a center, a line from the center to the vertex is the axis of the pyramid. A pyramid that has its axis perpendicular to its base is a right pyramid; otherwise, it is an oblique pyramid, then it is also a regular pyramid.

The altitude (h) of a pyramid is the perpendicular distance from the base to the vertex. The volume of any pyramid is l/3Ah,where A is the area of the base. In a regular pyramid all the lateral edges have the same length. The slant height (s) of the pyramid is the altitude of a face; the total surface areaof the lateral faces is l/2sp,where pis the perimeter of the base polygon.

XII. POLYHEDRON

A polyhedronis a surface composed of plane polygonal surfaces (faces).The sides of the polygons,joining two faces, are its edges.The corners, where three or more faces meet, are its vertices. Generally, the term

"polyhedron" is used for closed solidfigure. A convex polyhedron is one for which a plane containing any face does not cut other faces; otherwise the polyhedron is concave.

A regularpolyhedron is one that has identical (congruent)regular polygons forming its faces and has all its polyhedralangles congruent. There are only five possible convex regular polyhedra:

1)tetrahedron- four triangular faces,

2)cube- six square faces,

3)octahedron- eight triangular faces,

4)dodecahedron- twelve pentagonal faces,

5)icosahedron- twenty triangular faces.

The five regular solids played a significant part in Greek geometry. They were known to Plato and are often called Platonicsolids. Kepler used them in his complicated model of the solar system.

A uniformpolyhedron is a polyhedron that has identical polyhedral angles at all its vertices, and has all its faces formed by regular polygons (not necessarily of the same type). The five regular polyhedra are also uniform polyhedra. Right prismsand antiprisms that have regular polygons as bases are also uniform. In addition, there are thirteen semiregularpolyhedra, the so-called Archimediansolids. For example, the icosidodecahedronhas 32 faces - 20 triangles and 12 pentagons. It has 60 edges and 30 vertices, each vertex beeing the meeting point of two triangles and two pentagons.Another example is the truncatedcube, obtained by cutting the corners off a cube. If the corners are cut so that the new vertices lie at the centers of the edges of the original cube, a cuboctahedronresults. Truncatingthe cuboctahedron and "distorting" the rectangular faces into squares yields another Archimedian solid. Other uniform polyhedra can be generated by truncating the four other regular polyhedra or the icosidodecahedron.