Viii. Rays, angles, simple closed figures

1. You certainly remember that by extending a line segment in
one direction we obtain a ray. 2. Below is a picture of such an ex-­
tension.

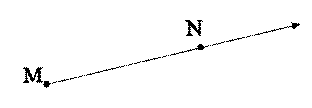
3. The arrow indicated that you start at point M, go through point N, and on without end. 4. This results in what is called ray MN_,which is denoted by the symbol MN. 5. Point M is the endpoint in this case. 6. Notice that the letter naming the endpoint of a ray is given when first naming the ray.

7. From what you already know you may deduce that drawing two rays originating from the same endpoint forms an angle. 8. The com­mon point of the two rays is the vertex of the angle.

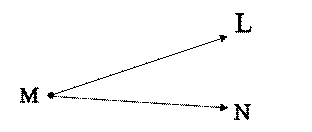
9. Angles, though open figures, separate the plane into three distinct sets of points: the interior, the exterior, and the angle. 10. The fol­lowing symbol Ð is frequently used in place of the word angle.

11. The angle pictured above could be named in either of the follo­wing ways: a) angle LMN (or ÐLMN); b) angle NML (or ∟NML).

12. The letter naming the vertex of an angle occurs as the middle
letter in naming each angle. 13. Look at the drawing below.

→ →

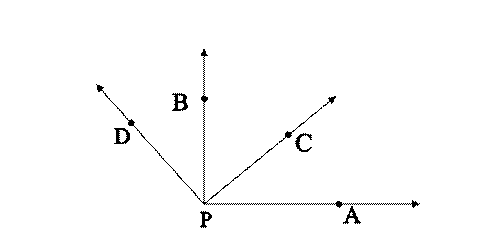
13. Ray PA (PA) and ray PB (PB) form a right angle, which means

→

that the angle has a measure of 90° (degrees). 15. Since PC
(except for point P) lies in the interior of ÐAPB, we speak of ÐCPA
being less than a right angle and call it an acute angle with a deg­ree

→

measure less than 90°. 16. Since PD (except for point P) lies in the exterior of ÐAPB, we say that ÐAPD is greater than a right angle and call it an obtuse angle with a degree measure greater than 90°.

Simple Closed Figures

17 A simple closed figure is any figure drawn in a plane in such a way that its boundary never crosses or intersects itself and encloses part of the plane. 18. The following are examples of simple closed figures. 19. Every simple closed figure separates the plane into three distinct sets of points. 20. The interior of the figure is the set of all points in the part of the plane enclosed by the figure. 21. The exterior of the figure is the set of points in the plane which are outside the figure. 22. And finally, the simple closed figure itself is still another set of points.

23. A simple closed figure formed by line segments is called a polygon. 24. Each of the line segments is called a side of the poly­gon. 25. Polygons may be classified according to the measures of the

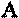
angles or the measure of the sides. 26. This is true of triangles — geometric figures having three sides — as-well as of quadrilaterals, having four sides.

27. In the picture above you can see three triangles. ∆ABC is referred to as an equilateral triangle. 29. The sides of such a triangle all have the same linear measure. 30. ∆DEF is called an isosceles triangle which means that its two sides have the same measure. 31. You can see it in the drawing above. 32. ∆ALMK being referred to as a right triangle means that it contains one right angle. 33. In ∆MKL, ÐM is the right angle, sides MK and ML are called the legs, and side KL is called the hypotenuse. 34. The hypote­nuse refers only to the side opposite to the right angle of a right triangle. Below you can see quadrilaterals.

35. A parallelogram is a quadrilateral whose opposite sides are parallel. 36. Then the set of all parallelograms is a subset of all quadrilaterals. Why? 37. A rectangle is a parallelogram in which all angles are right angles. 38. Therefore we can speak of the set of rec­tangles being a subset of the set of parallelograms. 39. A square is a rectangle having four congruent sides as well as four right angles. 40. Is every square a rectangle? Is every rectangle a square? Why or why not? 41. A rhombus is a parallelogram in which the four sides are congruent. 42. Thus, it is evident that opposite sides of a rhombus are parallel and congruent. 43. Is defining a square as a special type of rhombus possible? 44. A trapezoidal has only two pa­rallel sides. 45. They are called the bases of a trapezoidal.