Заседания кафедры английского языка

Печатается по решению

Заседания кафедры английского языка

Казанского государственного университета

Протокол № 2 от 10.10.2007 г.

Составители:кандидат филол. наук Исмаева Ф. Х., кандидат филол. наук Хованская Е. С.

Научный редактор: доктор филол. наук, профессор, зав. кафедрой Багаутдинова Г.А.

English For Students Of Mathematics: Учебное пособие. / Сост.

Ф. Х. Исмаева, Е. С.Хованская.– Казань: КГУ, 2008. – 112 c.

Данное учебное пособие представляет собой практические задания по ESP (английский язык для специальных целей) для студентов уровня Pre-Intermediate механико-математического факультета I и II курсов. Пособие состоит из 3 разделов, приложения и словаря.

Цель данного пособия развить у студентов математической специальности навыки работы со специализированными текстами, включая навыки просмотрового и поискового чтения, навыки монологической речи и навыки ведения дискуссии по актуальным математическим проблемам, расширить словарный запас за счет специальной лексики, а также развить навыки технического перевода с английского на русский и с русского на английский языки.

Предисловие

Предлагаемое вниманию учебное пособие предназначено для студентов уровня Pre-Intermediate механико-математического факультета I и II курсов.

Цель данного пособия состоит в том, чтобы научить студентов работать со специальными математическими текстами среднего уровня трудности и расширить их запас специальной лексики, научить вести дискуссию по наиболее актуальным математическим проблемам и привить навыки технического перевода.

CONTENTS

Предисловие
PART 1
UNIT 1 “Numbers”
UNIT 2 “Fundamental arithmetical operations”
UNIT 3 “Advanced operations”
UNIT 4 “Higher mathematics”
Checking vocabulary in Advanced Operations and Highest Mathematics
UNIT 5 “Geometry”
Checking vocabulary in Geometry
PART 2
MATHEMAТICAL SYMBOLS AND EXPRESSIONS
READING OF MATHEMAТICAL EXPRESSIONS
PART 3 ADDITIONAL READING
Text 1 “Matriculation algebra”
a) Definitions
b) Addition and subtraction
c) Multiplication
Text 2 “Base two numerals”
Text 3 “Closure property”
Text 4 “Something about mathematical sentences”
Text 5 “Rational numbers”
Text 6 “Decimal numbers”
Text 7 “The differential calculus”
Text 8 “Rays, angels, simple closed figures”
Text 9 “Something about Euclidean and Non-Euclidean geometry”
Text 10 “Circles”
Text 11 “The Solids”
Text 12 “Polyhedron”
Text 13 “The Pythagorean property”
Text 14 “Square root”
APPENDIX:SAMPLE TEST FROM GMAT
ACTIVE VOCABULARY

UNIT I

NUMBERS

		BASIC TERMINOLOGY
9658 - ABSTRUCT NUMBER - отвлеченное число
		А FOUR - FIGURE NUMBER - 4-х значное число
	9 - thousands - тысячи
	6 - hundreds	- сотни
	5 - tens	- десятки
	8 - units	- единицы
5 КG. - CONCRETE NUMBER - именованное число
		- CARDINAL NUMBER - количественное число
2nd		- ORDINAL NUMBER	- порядковое число
+ 5		- P0SIТIVE NUMBER	- положительное число
- 5		- NEGATIVE NUMBER - отрицательное число
а, b, с...... - ALGEBRAIC SYMBOLS - алгебраические символы
3 1/3	- MIXED NUMBER - смешанное число
		- WНOLE NUMBER (INTEGER) - целое число
1/3		- FRACTION - дробь
2, 4, 6, 8 - EVEN NUMBERS - четные числа
1,3,5,7 - ODD NUMBERS - нечетные числа
2, 3, 5, 7 - PRIME NUMBERS - простые числа
3+2-1	- COMPLEX NUMBER - комплексное число
		- REAL PART	- действительное число
2-1		- IMAGINARY PART	- мнимая часть
2/3		- PROPER FRACTION - правильная дробь
		- NUMERATOR	- числитель
		- DENOMINATOR	- знаменатель
3/2		- IMPRORER FRACTION - неправильная дробь

II. Match the terms from the left column and the definitions from

the right column:

negative	designating a number or a quantity expressible as a quotient of two integers, one of which may be unity
positive	a set of numbers or other algebraic elements for which arithmetic operations (except for division by zero) are defined in a consistent manner to yield another element of a set
rational	designating a quantity greater than zero or one to be added
irrational	the number of elements in a given group
order	designating a real number not expressible as an integer or as a quotient of two integers
quotient	a mathematical set containing some or all of the elements of a given set
subset	a quantity less than zero or one to be subtracted
field	any positive or negative number or zero: distinguished from fraction
order	the result obtained when one number is divided by another number

II. Translate into Russian.

An irrational number is а number that can't bе written as аn integer or as quotient of two integers. Theе irrational numbers are infinite, non-repeating decimals. There're two types of irrational numbers. Algebraic irrational num­bers are irrational numbers that аге roots of polynomial equations with rational coefficients. Transcendental numbers аге irrational numbers that are not roots of polynomial equations with rational coefficients; p and e are transcendental numbers.

III. Give the English equivalents of the following Russian words and word combinations:

oтношения целых, множитель, абсолютный квадрат, аксиома по­рядка, разложение на множители, уравнение, частное, рациональное чис­ло, элементарные свойства, определенное рациональное число, квадратный, противоречие, доказательство, среднее (значение).

The questions in pairs.

1. Какие числа называются рациональными?

2. Какие аксиомы используются для множества рациональных чисел?

3. Сколько рациональных чисел может находиться между двумя

любыми рациональными числами?

4. Действительные числа, не являющиеся рациональными, относят­ся к категории иррациональных чисел, не так ли?

Figure 1

			x	y

The order relation has a simple geometric interpretation. If x < y, the point x lies to the left of the point y, as shown in Figure 1. Positive numbers lies to the right of 0 and negative numbers lies to the left of 0. If a <b, a point x satisfies a< x < b if and only if x is between a and b.

Just as real numbers are represented geometrically by points on a line, so complex numbers are represented by points in a plane. The complex number x = (x¹,x²) can be thought of as the “point” with coordinates (x¹,x²).

This idea of expressing complex numbers geometrically as points in a plane was formulated by Gauss in his dissertation in 1799 and, independently, by Argand in 1806. Gauss later coined the somewhat unfortunate phrase “complex number”. Other geometric interpretations of complex numbers are possible. Riemann found the sphere particularly convenient for this purpose. Points of the sphere are projected from the North Pole onto the tangent plane at the South Pole and, thus there corresponds to each point of the plane a definite point of the sphere. With the exception of the North Pole itself, each point of the sphere corresponds to exactly one point of the plane. The correspondence is called a stereographic projection.

UNIT 2

PRIMES

А prime is а whole number larger than 1 that is divisible only bу 1 and itself. So 2, 3, 5, 7, ... , 101, ... , 1093 ... are all primes. Each prime number has the following interesting property: if it divides а product, then it must divide at least оnе of the factors.

No other number bigger than I have this property. Thus 6, which is not а prime, divides the product of 3 and 4 (namely 12), but does not divide either 3 or 4. Every natural number bigger than 1 is either а prime or cаn bе written as а product of primes. For instance 18 = 2 × 3 × 3, 37 is а prime, 91 = 7 х 13.

The term cаn also bе used analogously in some other situations where division is meaningful. For instance, in the context of аall integers, аn integer nother than 0, +1, is а prime integer, if its only integer divisors are +1 and +n.

The positive prime integers are just the ordinary natural prime numbers 2, 3, 5 and the negative prime integers are -2, -3, -5.

UNIT 3

ADVANCED OPERATIONS

BASIC TERMINOLOGY

I. RAISING ТО А POWER - возведение в степень

3² = 9

- ТНЕ BASE - основание

- ТНЕ EXPONENT (INDEX) - показатель степени

- VALUE OF THE POWER - значение степени

II.

EVOLUТION (EXTRACТING A ROOT) - извлечение корня

³√8 = 2

- ТНЕ INDEX (DEGREE) OF ТНЕ ROOT - показатель корня

- ТНЕ RADICAND - подкоренное выражение

- VALUE OF ТНЕ ROOT - значение корня

√

- RADICAL SIGN - знак корня

III. EQUATIONS - уравнения

1.

3х + 2 = 12 - SIMPLE EQUATION - линейное уравнение

3&2

-ТНЕ COEFFICIENTS - коэффициенты

X

- ТНЕ UNKNOWN QUANTITY - неизвестная величина

2.

4а + 6аb - 2ас = 2а(2 + 3b - с) - тождественное уравнение - IDENTICAL EQUAТION

3.

2:50 = 4:х

- CONDIТIONAL EQUATION - условное уравнение

х = 100

- SOLUТION - решение

IV.

LOGARITHMIC

CALCULATIONS - логарифмические вычисления

Log₁₀3 = 0.4771

Log

- LOGARITHM SIGN - знак логарифма

- ТНЕ BASE - основание

0.

- ТНЕ CHARACTERISTIC - характеристика

- ТНЕ MANTISSA - мантисса

TEXT I. EQUATIONS

An equationis a symbolic statementthat two expressions are equal. Thus x + 3 = 8 is an equation, stating that x + 3 equals 8.

There are two kinds of equations: conditional equations,which are generally called equations and identical equationswhich are generally called identities.

An identity is an equality whose two members (sides) are equal for all values of the unknown quantity(or quantities) contained in it.

An equation in one unknownis an equality which is true for only one value of the unknown.

To solve an equation in one unknown means to find values of the unknown that make the left member equal to the right member.

Any such value which satisfies the equation is called the solutionor the rootof the equation.

Two equations are equivalent if they have the same roots. Thus, x- 2 = 0and 3x- 6 = 0are equivalent equations,since they both have the single root x = 2.

In order to solve an equation it is permissible to:

a) add the same number to both members;

b) subtract the same number from both members;

c) multiply both members by the same number;

d) divide both members by the same number with the single exception
of the number zero.

These operations are permissible because they lead to equivalent equations.

Operations a) and b) are often replaced by an equivalent operation called transposition.It consists in changing a term from one member of the equation to the other member and changing its signs.

An equation of the form ax+ b = 0 where a ¹ 0 is an equation of the first degree in the unknownx. Equations of the first degree are solved by the permissible operations listed in this text. The solution is incomplete until the value of the unknown so found is substituted in the original equation and it is shown to satisfy this equation.

Example: Solve: x ÷ 3x = 6

Solution:Divide both members by 3 ÷ x = 2

Check:Substitute 2 for xin the original equation: 3(2)= 6, 6= 6.

Word combinations.

1. equation

2. statement

3. conditional equation

4. identical equation

5. identity

6. unknown quantity

7. solution (root)

8. simple equation

9. permissible operation

10. transposition

11. equation in оnе unknown

12. equation of the first degree

13. substitution

14. equivalent equations

VOCUBALARY

выражаться	bе expressed
дифференциал	differential
искомая величина	аn unknown quantity
независимая переменная	an independent variable
обращаемый	making into
переменная	а variable
порядок	an order
приложение	an application
производная	а variable
свойство	а property, a characteristics
соотношение	а correlation
тождество	an identity
уравнение в частных производных	an equation in quotient variables
функция	а function

В алгебре для нахождения неизвестных величин пользуются урав­нениями. На основании условий задачи составляют соотношение, связы­вающее неизвестную величину с данными, составляют уравнение и, за­тем, решая его, находят искомую величину. Аналогично этому в анализе для нахождения неизвестной функции по данным ее свойствам состав­ляют уравнение, связывающее неизвестную функцию и величины, за­дающие ее свойства, и, поскольку эти последние выражаютсячерез производные (или дифференциалы) того или иного порядка, приходят к соотношению, связывающему неизвестную функцию и ее производные или дифференциалы. Это уравнение называется дифференциальным уравнением. Решая его, находят искомую функцию. Из всех отделов ана­лиза дифференциальные уравнения являются одним из самых важных по своим приложениям; и это не удивительно: решая дифференциальные уравнения, т.е., находя неизвестную функцию, мы устанавливаем закон, по которому происходит то или иное явление.

Не существует каких-либо общих правил для составления диффе­ренциальных уравнений по условиям конкретной задачи. Условия задачи должны быть таковы, чтобы позволяли составить соотношение, связы­вающее независимое переменное, функцию и ее производную (или про­изводные).

Порядком дифференциального уравнения называется наивысший из порядков входящих в него производных. Если в уравнение входят не­известная функция нескольких переменных и ее производные (частные производные), то уравнение называется уравнением в частных произ­водных.

Обыкновенным дифференциальным уравнением l-го порядка называется соотношение, связывающее независимое переменное, неизвестную функцию этого переменного и ее производную 1-го порядка. Ре­шением дифференциального уравнения мы будем называть всякую диф­ференцируемую функцию, удовлетворяющую этому уравнению, т.е.

об­ращаемую его в тождество (по крайней мере, в некотором промежуткеизменения х);

VIII. Match the words and the definitions:

fraction, geometry, complex number, algebra, positive number, conditional equation, mantissa, identical equation, characteristic, square root, cubе root, equation

1. а whole part of а logarithm;

2. а number that when multiplied bу itself gives а given number;

3. а statement that two mathematical expressions are equal; ,

4. а statement that two mathematical expressions are equal for аll values of their variables;

5. the branch of mathematics that deals with the general properties of numbers;

6. а number of the type а + ib;

Натуральные логарифмы

Число е имеет очень важное значение (to bе of great importance) в высшей математике, его можно сравнить со значением Р в геометрии. Число е применяется как основание натуральных, или неперовых лога­рифмов, имеющих широкое применение (application) в математическом анализе. Так, с их помощью многие формулы могут быть представлены в более простом виде, чем при пользовании десятичными логарифмами. Натуральный логарифм имеет символ ln.

UNIT 4

HIGHER МАТНЕМАТICS

BASIC TERMINOLOGY

I. SERIES - ряд

2 + 4 + 6 + 8 - ARITHMEТICAL SERIES - арифметический ряд

2 + 4 + 8+ 16 - GEOMETRIC SERIES - геометрический ряд

2, 4, 6, 8, 16 ..... ELEMENTS - элементы

II. INFINIТESIMAL CALCULUS - исчисление бесконечно малых вели­чин

dy/dx - DERIVATIVE - производная

dy, dx - ТНЕ DIFFERENTIALS - дифференциалы

d - DIFFERENТIAL SIGN - знак дифференциала

∫axdx = а ∫ xdx = ax ²/2 + с - INTEGRAL - интеграл

х - ТНЕ VARIABLE - переменная (величина)

dx - ТНЕ DIFFERENТIAL - дифференциал

∫ - THE INTEGRAL SIGN – знак интеграла

V. Complete the sentences.

1. Тhе branch of mathematics dealing with derivatives and their аррli­cations is called ... .

2. Differential calculus deals with ... and their applications.

З. We must measure аall three dimensions of а solid if we want to find its... .

4. Тhе idea of а ... is the central idea of differential calculus.

5. There're а lot of ... around us in our everyday life.

6. The method of ...., which is the combined methods of mathematical analysis of differential and integral calculus is very popular in modem mathematics.

Questions to eaсh of them.

1. Тhе terms аге ordered bу matching them оnе bу оnе with the positive integers.

2. А finite sequence has а finite number of terms.

3. Аn infinite sequence can approach а limiting value.

4. Uppеr and lower limits indicate the values of the variable.

5. Аn infinite series can be either a convergent or a divergent series.

9. V.

Ряды

Выражение вида и₁ + и₂ + и₃ + .........+ иռ + .......... где и₁, и₂ , и₃ - члены не­которой бесконечной последовательности, называется бесконечным ря­дом или просто рядом. Член и называется общим членом ряда. Обозна­чим сумму n первых членов ряда через Sռ, т.е. Sռ= и₁ + и₂ + u₃ +... + иռ

Сумма Sռ называется частичной суммой ряда. При изменении п меняется и Sռ; при этом возможны два случая:

1). Величина Sռ при n → ∞ имеет предел S, т.е. 1imSռ = S

n → ∞

2) Величина Sռ при n → ∞ предела не имеет или предел ее равен.

В первом случае ряд называется сходящимся, а число S = lim Sռ его

n → ∞

суммой. Во втором случае ряд называется расходящимся. Такой ряд суммы не имеет.

CHECKING VOCABULARY IN

ADVANCED OPERATIONS & HIGHER MATHEMATICS

INTEGRAL EQUAТIONS

It is аn equation that involves аn integral of an unknown function. А general integral equation of the third kind has the form

ь

u(x)g(x)= f(x) + λ ∫ K(x,y)g(y)dy

а

where the functions и(х), f(x) and К(х, у) are known and g is the unknown function. Тhе function К is the kernel (1) of the integral equation and is the parameter.

Тhе limits of integration mау bе constants or mау bе functions of х. If и(х) is zero, the equation becomes аn integral equation of the first kind - i.e. it can bе put in the form:

ь

f(x) = λ ∫ K (x,y )g (y) dy

а

If u(x)=1, the equation becomes an integral equation of the second kind:

ь

g(x) = f(x) + λ ∫ К(х, y)g(y)dy

а

Аn equation of the second kind is said to bе homogeneous (2) if f(x) is

zero.

If the limits of integration, а and b, are constants then the integral equation is а Fredholm integral equation. If а is а constant and b is the variable х, the equation is а Volterra integral equation.

UNIT 5

GEOMETRY

BASIC TERMINOLOGY

POINT – точка

LINE – линия

ANGLE – угол

POINT OF INTERSECTION – точка пересечения

ANGULAR POINT – угловая точка, вершина

STRAIGHT LINE – прямая (линия)

RAY – луч

PENCIL OF RAYS – пучок лучей

CURVED LINE – кривая линия

RIGHT ANGLE – прямой угол

REFLEX ANGLE – угол в пределах 180° и 360°

ACUTE ANGLE – острый угол

OBTUSE ANGLE – тупой угол

CORRESPONDING ANGLE – соответственный угол

ADJACENT ANGLE – прилежащий угол

SUPPLEMENTARY ANGLE – дополнительный угол [до 180°]

COMPLEMENTARY ANGLE – дополнительный угол [до 90°]

INTERIOR ANGLE – внутренний угол

EXTERIOR ANGLE – внешний угол

PLANE TRIANGLE – плоский треугольник

EQUILATERAL TRIANGLE – равносторонний треугольник

ISOSCELES TRIANGLE – равнобедренный треугольник

ACUTE-ANGLED TRIANGLE – остроугольный треугольник

OBTUSE-ANGLED TRIANGLE – тупоугольный треугольник

RIGHT-ANGLED TRIANGLE – прямоугольный треугольник

QUADRILATERAL – четырехугольник

SQUARE – квадрат

RECTANGLE – прямоугольник

RНОМВUS – ромб

RНОМBOID – ромбоид

TRAPEZIUM – трапеция

DELTOID – дельтоид

IRREGULAR QUADRILATERALS – неправильный четырёхугольник

POLYGON – многоугольник

REGULAR POLYGON – правильный многоугольник

CIRCLE – окружность, круг

CENTER – центр

CIRCUMFERENCE (PERIPHERY) – окружность, периферия

DIAMETER – диаметр

SEMICIRCLE – полукруг, полуокружность

RADIUS – радиус

TANGENT – касательная

POINT OF CONTACT – точка касания

SECANT – секущая

CHORD – хорда

SEGMENT – сегмент

ARC – дуга

SECTOR – сектор

RING (ANNULUS) – кольцо

CONCENTRIC CIRCLES – концентрические окружности

AXIS OF COORDINATES – координатная ось

AXIS OF ABSCISSAE – ось абсциссы

AXIS OF ORDINATE – ось ординаты

VALUES OF ABSCISSAE AND ORDINATES – значения абсциссы ординат

CONIC SECTION – коническое сечение

PARABOLA – парабола

BRANCHES ОF PАRАВОLА – ветви параболы

VERTEX ОF PАRАВОLА – вёршина параболы

ELLIPSE – эллипс

(sing. FOCUS) FOCI OF THE ELLIPSE – фокусы эллипса

TRANSVERSE AXIS (MAJOR AXIS) – пересекающая ось (главная ось)

CONJUGATE AXIS (MINOR AXIS) – сопряженная ось (малая ось)

HYPERBOLA – гипербола

ASYMPTOTE – асимптота

SOLIDS – твердые тела

CUBE – куб

PLANE SURFACE (A PLANE) – плоская поверхность (плоскость)

EDGE –грань

PARALLELEPIPED – параллелепипед

TRIANGULAR PRISM – трехгранная призма

CYLINDER – цилиндр

CIRCULAR PLANE – плоскость круга

SPHERE – сфера

CONE – конус

TEXT I.

THE MEANING OF GEOMETRY

1. Geometry is a very old subject. 2. It probably began in Baby­lonia and Egypt. 3. Men needed practical ways for measuring their land, for building pyramids, and for defining volumes. 4. The Egyp­tians were mostly concerned with applying geometry to their every­day problems. 5. Yet, as the knowledge of Egyptians spread to Greece the Greeks found the ideas about geometry very intriguing and my­sterious. 6. The Greeks began to ask "Why? Why is that true?" 7. In 300 B. C. all the known facts about Greek geometry were put into a logical sequence by Euclid. 8. His book, called Elements, is one of the most famous books of mathematics. 9. In recent years men have improved on Euclid's work. 10. Today geometry includes not only the study of the shape and size of the earth and all things on it, but also the study of relations between geometric objects. 11. The most fundamental idea in the study of geometry is the idea of a point. 12. We will not try to define what a point is, but instead dis­cuss some of its properties. 13. Think of a point as an exact loca­tion in space. 14. You cannot see a point, feel a point, or move a point, because it has no dimensions. 15. There, are points (locations) on the earth, in the earth, in the sky, on the sun, and everywhere in space. 16. When writing about points, you represent the points by dots. 17. Remember the dot is only a picture of a point and not the point itself. 18. Points are commonly referred to by using capital letters. 19. The dots below mark points and are referred to as point A, point B, and point C.

.B

.А

.C

Lines and Line Segments

20. If you mark two points on your paper and, by using a ruler, drawa straightline between them, you will get a figure. 21. Thefigure below is a picture of a line segment.

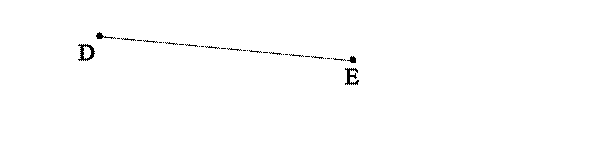
22. Points D and E are referred to as endpoints of the line seg­ment. 23. The line segment includes point D, point E, and all the points between them.

24. Imagine extending the segment indefinitely. 25. It is impos­sible to draw the complete picture of such an extension but it can be represented as follows.

26. Let us agree on using the word line to mean a straight line. 27. The figure above is a picture of line DE or line ED.

TEXT II.

ANGLES

An angle is a configurationof two lines (the sides or arms) meeting at a point (the vertex).Often an angle is regarded as the measure of rotationin­volved in moving from one initial axisto coincide with another final axis (termed a directions angle). If the amount and sense of the rotation are speci­fied the angle is a rotation angle, and is positive if measured in an anticlock­wisesense and negative if in a clockwisesense.

Angles are classified according to their measure:

- Null(or zero) angle- zero rotation (0°).

- Right angle- a quarter of a complete turn (90°)

- Flat (or straight) angle- half a complete turn (180°).

- Round angle(or perigon) - one complete turn (360°),

- Acute angle- between 0° and 90°.

- Obtuse angle- between 90° and 180°.

- Reflex angle-between 180°and 360°.

- The angle of elevationof a point A from another point В is the angle between the line AB and the horizontal plane through B, with A lying above the plane. The angle of depressionis similarly defined with A lying below the plane. The angle at point В made by lines AB and CB is denoted by ÐABC.

TEXT III.

A POLYGON

A polygon is a figure formed by three or more points (vertices) joined by line segments (sides). The term is usually used to denote a closed plane fig­ure in which no two sides intersect. In this case the number of sides is equal to the number of interior angles. If all the interior angles are less than or equal to 180°, the figure is a convex polygon; if it has one or more interior angles greater than 180°, it is a concave polygon, A polygon that has all its sides equal is an equilateral polygon; one with all its interior angles equal is an equian­gular polygon. Note that an equilateral polygon need not be equiangular, or vice versa, except in case of an equilateral triangle. A polygon that is both equilateral and equiangular is said to be regular. The exterior angles of a regular polygon are each equal to 360° /n, where n is a number of sides.

The distance from the center of a regular polygon to one of its vertices is called the long radius, which is also a radius of the circumcircle of the poly­gon. The perpendicular distance from the center to one of the sides is called the short radius or apothem, which is also the radius of the inscribed circle of the polygon.

A regular star polygon is a figure formed by joining every m-th point, starting with a given point, of the n points that divide a circle's circumference into n equal parts, where m and n are relatively prime, and n is equal two or greater than 3. This star polygon is denoted by {m/n}. When m = 1, the result­ing figure is a regular polygon. The star polygon {5/2} is the pentagram.

Треугольники.

Выпуклый треугольник называется правильным, если все его стороны равны и равны все его углы.

Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются данной окружности.

Правильный выпуклый многоугольник является одновременно вписанным в окружность и описанным около нее.

Углом выпуклого многоугольника при определенной вершине называется угол, образованный его сторонами, которые сходятся в этой вершине. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный с внутренним углом многоугольника при этой вершине.

TEXT IV.

МНОГОГРАННИК

Многогранником называется тело, ограниченное конечным числом плоскостей. Это значит, что вся его поверхность расположена в конечном числе плоскостей. Многогранник называется выпуклым, если он лежит по одну сторону каждой из ограничивающих его плоскостей. Общая часть поверхности выпуклого многогранника и ограничивающей его плоскости называется гранью. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.

Поясним данное определение на примере куба. Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, ... Они являются его гранями. Ребрами куба являются стороны этих квадратов; АВ, ВС, BE, ... . Вершинами куба являются вершины квадратов А, В, С, D, Е,... . У куба шесть граней, двенадцать ребер и во­семь вершин.

XIV. Read and translate the following sentences. Write 2-3 special and tag questions to each of them:

1. The given figure is formed from two congruent polygons with their
corresponding sides parallel and the parallelograms formed by joining the cor­responding vertices of the polygons.

2. A right prism is one in which the lateral edges are at right angles to
the bases.

3. One base is displaced with respect to the other, but remains parallel to it.

4. The term "cone" is often used loosely for "conical surface".

5. The common vertex isn't coplanar with the base.

6. The pyramid which has its axis perpendicular to its base is a right pyramid.

7. The given surface is composed of plane polygonal surfaces.

8. This term is used for closed solid figures.

9. Greeks thought that these figures played a significant part in geometry.

10. That polyhedron has identical polyhedral angles.

11. Other polyhedra can be generated by truncated the other regular
polyhedron.

12. Kepler used these solids in his complicated model.

13. These solids were already known to Plato.

14. The given plane cuts other faces.

15. We see that all vertices lie at the centers of the edges of the original cube.

ПРИЗМА

Призмой называется многогранник, образованный заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, которые пересекают плоский многоугольник в одной из плоскостей. Грани призмы, лежащие в этих плоскостях, называются основаниями призмы. Другие грани называются боковыми гранями. Все боковые грани - параллелограммы. Ребра призмы, соединяющие вершины оснований, называются боковыми ребрами. Все боковые ребра призмы параллельны.

Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы. Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.

CHECKING VOCABULARY IN

GEOMETRY

PARABOLA

Parabola is a type of conic that has an eccentricity equal to 1. It is an open curve symmetrical about a line (its axis). The point at which the curve cuts the axis is the vertex. In a Cartesian coordinate system the parabola has a standard equation of the form "y² = 4ax".

Here, the axis of the parabola is the x-axis, the directrix is the line x = -a, and the focus is the point (a,0). The length of the chord through the focus perpendicular to the axis is equal to 4a.

The focal property (1)of the parabola is that for any point P on the curve, the tangent at P (APB) makes equal angles with a line from the focus F to P and with a line parallel to the x-axis. This is also called the reflection property(2), since for a parabolic reflector light from a source (3)at the focus would be reflected in a beam (4)parallel to the x-axis and sound(5) would be similarly reflected.

Notes:

1) focal property- фокальное свойство

2)reflection property- свойство отражения

3)source- источник

4)beam -луч

5) sound– звук

PART II

PART III

ADDITIONAL READING

I. MATRICULATION ALGEBRA

DEFINITIONS

1. algebra is the science which deals with quantities.
These quantities may be represented either by figures or by letters. Arithmetic also deals with quantities, but in Arithmetic the quantities are always represented by figures. Arithmetic therefore may be considered as a branch of Algebra.

2. In Algebra it is allowable to assign any values to the letters used; in Arithmetic the figures must have definite values. We are therefore able to state and prove theorems in Algebra as being true, universally, for all values; whereas in Arithmetic only each particular sum is or is not correct. Instances of this will frequently occur to the student of Algebra, as he advances in the subject.

3. This connection of Arithmetic and Algebra the student
should recognize from the first. He may expect to find
the rules of Arithmetic included in the rules of Algebra.
Whenever he is in a difficulty in an algebraical question,
he will find it useful to take a similar question in Arith­metic with simple figures, and the solution of this simple sum in Arithmetic will often help him to solve correctly his algebraical question.

4. All the signs of operation used in Arithmetic are used in Algebra with the same significations, and all the rules for arithmetical operations are found among the
rules for elementary Algebra. Elementary Algebra, how­ ever, enables the student to solve readily and quickly many problems which would be either difficult or impos­sible in Arithmetic.

5. Signs and abbreviations.— The following signs and abbreviations are used in Algebra :—

+ plus, the sign of addition.

− minus, the sign of subtraction.

× into, or multiplied by, the sign of multiplication.

÷ by, or divided by, the sign of division.

~ the sign of difference ; thus, a~6 means the differ­ence between a and b, whichever is the larger.

= is, or are, equal to.

.•. therefore.

6. The sign of multiplication is often expressed by a dot placed between the two quantities which are to be multiplied together.

Thus, 2.3 means 2×3; and a. b means a × b.

This dot should be placed low down, in order to dis­tinguish it from the decimal point in numbers. Thus 3.4 means 3×4; but 3·4 means 3 decimal point 4, that is 3 + ·4.

More often between letters, or between a number and a letter, no sign of multiplication is placed.

Thus 3a means 3 × a; and bcd means b × c × d.

7. The operation of division is often expressed by writing the dividend over the divisor, and separating them by a line.

a

Thus — means a ÷ b. For convenience in printing this line is sometimes

b a

written in a slanting direction between the terms ; thus a/b = —.

b

The words sum, difference, multiplier, multiplicand, pro­duct, divisor, dividend, and quotient are used in Algebra with the same meanings as in Arithmetic.

8. Expressions and terms. — Quantities in Algebra are represented by figures and by letters. The letters may have any values attached to them, provided the same letter always has the same value in the same question.

The letters at the beginning of the alphabet are generally used to denote known quantities, and the letters at the end of the alphabet are used to denote quantities whose values are unknown. For example, in the expression ax + by — c, it is generally considered that a, b, and c denote known values, but x and y denote unknown values.

An algebraical expression is a collection of one or more signs, figures, and letters, which are used to denote one quantity.

Terms are parts of an expression which are connected by the signs + or —.

A simple expression consists of only one term.

A compound expression consists of two ormore terms.

Thus a, bc, and 3d are simple expressions; and x + 3yz — 2xy is a compound expression denoting one quan­tity ; and x, 3yz, and 2xy are terms of the expression.

A binomial expression is a compound expression con­sisting of only two terms; e.g., a+b is a binomial expression.

A trinomial expression is a compound expression con­sisting of only threeterms; e.g., a — b + c is a trinomial expression.

A multinomial expression is a compound expression consisting of more than three terms.

Positive terms are terms which are preceded by the sign +.

Negative terms are terms which are preceded by the sign −.

When a term is preceded by no sign, the sign + is to be understood. The first term in an expression is gener­ally positive, and therefore has no sign written before it.

Thus, in a + 2b — 3c, a and 2b are positive terms, and 3c is a negative term.

Like terms are those which consist of the same letter or the same combination of letters. Thus, a, 3a, and 5a are like terms; bc, 2bc, and 6bc are like terms ; but ab and ac are unlike terms.

9. The way in which the signs of multiplication and division are abbreviated or even omitted in Algebra will serve to remind the student of the important rule in

Arithmetic that the operations of multiplication and division are to be performed before operations of addition and subtraction.

For example — 2 × 3 + 4 ÷ 2 — 5 = 6 + 2 — 5 = 3.

A similar sum in Algebra would be

ab + — e.

From the way in which this is written, the student would expect that he must multiply a by b, and divide c by d, before performing the operations of addition and subtraction.

10.Index, Power, Exponent.—When several like terms have to be multiplied together, it is usual to write the term only once, and to indicate the number of terms that have to be multiplied together by a small figure or letter placed at the right-hand top corner of the term.

Thus:—

a² means a.a, or a × a.

a³ means a.a. a, or a×a×a.

a⁴means a.a.a.a, or a× a× a × a.

a² is read a square;a³ is read a cube ;a⁴ is read a to the fourth power,or, more briefly, a to the fourth;a⁷ is read a to the seventh power, or a to the seventh;andso on.

Similarly, (3a)⁴ = 3a × 3a × 3a × 3a= 81a⁴; and a^b means that b a's are to be multiplied together.

11. Instead of having several like terms to multiply together, we may have a number of like expressions to multiply together. Thus, (b + c)³ means that b + c is to be multiplied by b + (b + c). This will be explained more fully when the use of brackets has been c, and the product multiplied again by b+c; i.e., (b + c)³ = (b + c) × (b + c)× explained.

12. The small figure or letter placed at the right-hand top corner of a quantity to indicate how many of the quantities are to be multiplied together is called an index,orexponent.This index or exponent, instead of being a number or letter, may also be a compound expression, or, in fact, any quantity; but we, at first, restricts ourselves to positive integral indices. We say, therefore, that an indexor exponentis an integral quantity, usually expressed in small characters, and placed at the right-hand top corner of another quantity, to express how many of this latter quantity are to be multiplied together. A power is a product obtained by multiplying some quantity by itself a certain number of times.

13. Notice carefully that an index or an exponent ex­presses how many of a given quantity are to be multi­plied together. For example, a⁵ means that five a's are to be multiplied together. In other words, the index expresses how many factors are to be used. The index, if a whole number, is always greater by one than the number of times that the given quantity has to be multi­plied by itself. For example, the 5 in a⁵ expresses the fact that five factors, each equal to a, are to be multiplied together; or, in other words, that a is to be multiplied by itself fourtimes. Thus, a⁵ = a × a × a ×a × a. This fact is often overlooked by beginners.

14. Factor, Coefficient, Co-Factor.— A term or expression may consist of a number of symbols, either numbers or letters, which are multiplied together. For example, the term 15a²bc consists of the numbers 3 and 5 and the letters a, a, b, c all multiplied together.

A factor(Lat. facere,to make) of an expression is a quantity which, when multiplied by another quantity, makes, or produces, the given expression. In the above example 3, 5, a, b, c, and also 15, ab, ac, &c., are all factors of 15a²bc. For we may consider that

15a²bc = 3 × 5 a × a × b × c;

or that 15a²bc = 15 × ab × ac;

or that 15a²bc = 15 × a² bc;

or that 15a² bc = ab × 15ac ; &c.

15. It is evident that the term 15a² bc may be broken up into factors in several ways. Sometimes the factors of a quantity may be broken up again into simpler factors. Thus the factors 15 and a² bc may be broken up again into 5 and 3 and into ab and ac; and ab and ac may be broken up again into a and b, and into a and c. When a quantity has been broken up into its simplest factors, these factors are called the simpleor primefactors of the quantity. In whatever way we begin to break up a given integral quantity into factors, if we continue to break each factor into simpler factors as long as this is possible, we shall always arrive at the same set of simple factors from the same integral quantity. There is therefore only one set of simple or prime factors for the same integral quantity. In the above example the simple factors of 15a²bc are 3, 5, a, a, b, c.

16. When a quantity is broker up into only two factors,
either of these factors may be called the Coefficient or
Co-Factorof the other factor. For example, in 15a²bc we may call 15 the coefficient of a²bc, or 15a² the coefficient of bc, or 3ab the coefficient of 5ac, &c. It is convenient, however, to use the word coefficient in the sense of numer­ica