Энтропийный способ измерения информации
Наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации называется теорией информации.
Любое сообщение, с которыми мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение, т.е. сообщение приобретает смысл тогда, когда состояние системы заранее неизвестно, случайно.
Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему, которая случайным образом может оказаться в том или ином состоянии, т.е. систему, которой заведомо присуща какая-то степень неопределенности.
Возникает вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?
Сравним между собой две системы, каждой из которых присуща некоторая неопределенность:
1) Монета, которая в результате бросания может оказаться в одном из двух состояний
2) Игральная кость, у которой 6 возможных состояний: 1, 2, 3, 4, 5, 6.
Неопределенность какой-то системы больше? Очевидно, второй, т.к. у нее больше возможных состояний, в каждом из которых система может оказаться с одинаковой вероятностью.
Может показаться, что степень неопределенности системы определяется числом возможных состояний системы. Но в общем случае это не так.
Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно; 2) отказало.
Пусть до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа – 0,01.
Такая система обладает очень малой степенью неопределенности: почти наверняка можно сказать, что устройство будет работать исправно.
При бросании монеты тоже имеется 2 возможных состояния, но степень неопределенности гораздо больше.
Таким образом, степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.
Перейдем к общему случаю.
Рассмотрим некоторую систему X, которая может принимать конечное множество состояний x1, x2, … xn с вероятностями p1, p2, … pn, где
pi = P(X ~ xi) – вероятность того, что система X примет состояние xi. Очевидно, 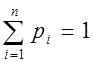 .
.
Запишем эти данные в виде таблицы
| xi | x1 | x2 | … | xn | |
| pi | p1 | p2 | pn |
В качестве меры априорной неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией.
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.
H(x)= – 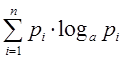 (1.1)
(1.1)
(знак «–» поставлен для того, чтобы энтропия была положительной; числа 0<pi<1 и их логарифмы отрицательны).
Логарифм может быть взят при любом основании a>1. Перемена основания равносильна умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 – о «двоичных единицах».
На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах. Это хорошо согласуется с применяемой в компьютерах двоичной системой счисления.
Энтропия системы, которая имеет два равновозможных состояния (в качестве основания логарифма выберем 2) равна единице:
H(X)= 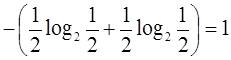
Определенная таким образом единица энтропии называется двоичной единицей и обозначается bit (от английского binary digit – двоичный знак)
Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.
Энтропия системы X, которая имеет n равновероятных состояний, измеренная в двоичных единицах, определяется по формуле (1.2)
H(X)= 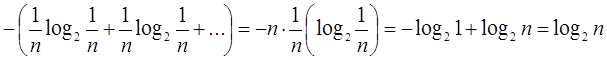 (1.2)
(1.2)
Таким образом
H(X)= 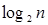 (1.3)
(1.3)
Т.е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.
Например, для системы с восемью состояниями
H(X) = 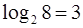
Свойства энтропии [1]:
1) Энтропия обращается в ноль, когда одно из состояний системы достоверно, а другие невозможны (действительно, в этом случае все вероятности p1, p2, …, pn обращаются в нуль, кроме одной, например, pk, которая равна единице. pk logpk = 1×log1 = 0)
2) При заданном числе состояний энтропия обращается в максимум, когда эти состояния равновероятны. При увеличении числа состояний энтропия увеличивается.
3) Свойство аддитивности. Когда несколько независимых систем объединяются в одну, их энтропии складываются.
Энтропия и информация
Итак, мы определили энтропию как меру неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем более содержательны сведения, тем больше информации о системе, тем менее неопределенным будет состояние системы.
Естественно поэтому количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
Рассмотрим некоторую системы Х, над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы Х становится полностью известным. До получения информации энтропия системы была H(X). После получения сведений состояние системы полностью определилось, т.е. энтропия стала равной нулю.
Обозначим Ix информацию, получаемую в результате выяснения состояния системы Х. Она равна уменьшению энтропии:
Ix=H(x) – 0
или
Ix = H(X), (1.4)
