Эквивалентные бесконечно малые

Для раскрытия неопределенностей вида 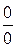часто бывает полезным применение эквивалентных бесконечно малых (функций).

Функции 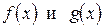называются эквивалентными бесконечно малыми при , если

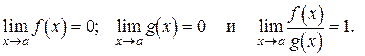
Эквивалентность двух функций обозначается волнистой чертой:

.

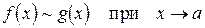При раскрытии неопределенности функцию или функции, входящие в предел, можно заменить на им эквивалентные:

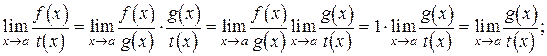
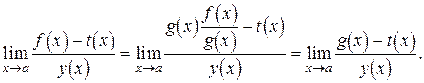
Замена во втором случае возможна, если 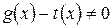. Используя замечательные пределы, можно составить таблицу эквивалентных бесконечно малых.

Таблица эквивалентных бесконечно малых

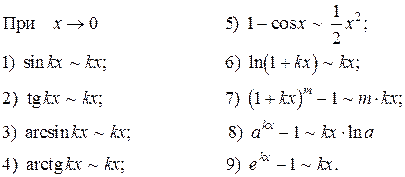
Приведем несколько примеров использования эквивалентных функций при вычислении пределов.

Пример 1.

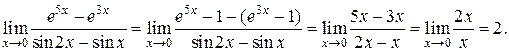
Пример 2.

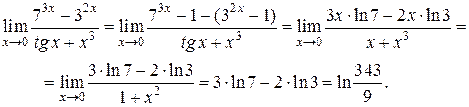
Пример 3.

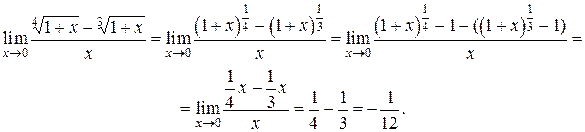
Производная функции одной переменной

Определение производной

Пусть функция 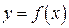определена на некотором промежутке. Возьмем значение 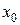из этого промежутка. Придадим 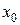какое-нибудь приращение 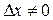(положительное или отрицательное). Этому новому значению аргумента соответствует и новое значение функции 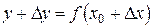, где .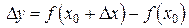

Составим отношение 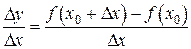, оно является функцией от .

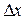Производной функции 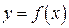по переменной в точке 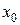называется предел отношения приращения функции 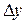в этой точке к вызвавшему его приращению аргумента 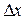, когда 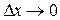произвольным образом:

.

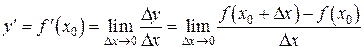Замечание. Считается, что производная функции в точке 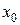существует, если предел в правой части формулы существует и конечен и не зависит от того, как приращение переменной стремится к 0 (слева или справа).

Процесс нахождения производной функции называется ее дифференцированием.

Механический и геометрический смысл производной

1) Скорость 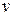прямолинейного движения точки есть производная пути 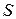по времени 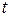: 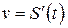. Это механический смысл производной. Поэтому производную любой функции называют скоростью изменения этой функции.

2) Угловой коэффициент невертикальной касательной к непрерывной кривой 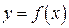в точке с абсциссой 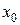есть производная 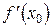, т.е. 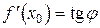. Это геометрический смысл производной.

Известно, что уравнение прямой, проходящей через точку 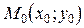с угловым коэффициентом 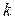имеет вид: 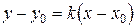. С учетом этой формулы уравнение касательной к кривой 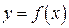в точке 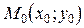принимает вид:

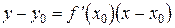
Нормалью к кривой в данной точке называется прямая, проходящая через данную точку перпендикулярно к касательной в этой точке.

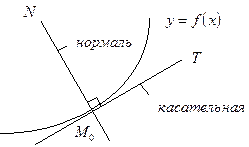Угловые коэффициенты взаимно перпендикулярных прямых связаны соотношением 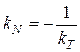, откуда 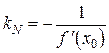. Следовательно, если 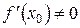, то уравнение нормали к кривой 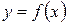в точке 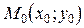можно записать в виде: .

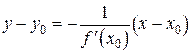Общие правила дифференцирования

Пусть функци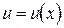и и 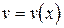дифференцируемы в точке . Тогда их сумма, разность, произведение и частное 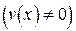также дифференцируемы в точке , причем

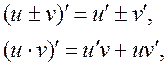
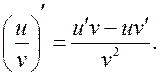
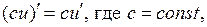
Таблица производных элементарных функций

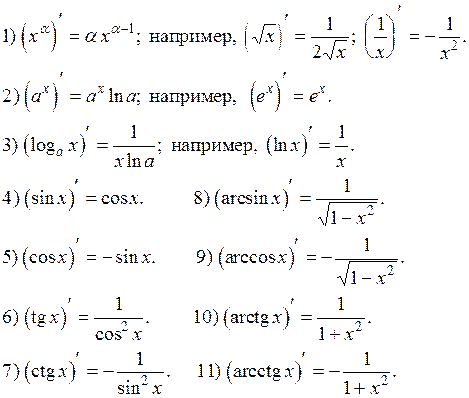
Замечание. Напомним свойства степеней и корней, используемые при дифференцировании функций:

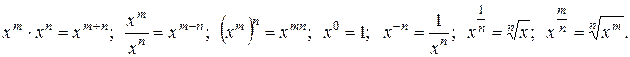
Приведем примеры нахождения производных.

1) .

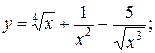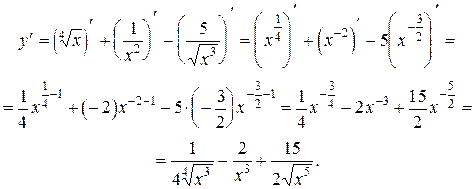
2)

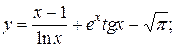
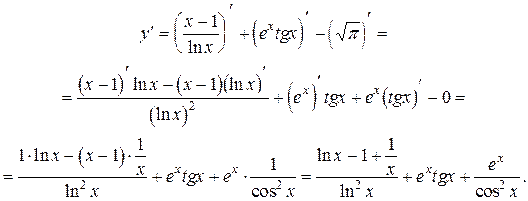
Производная сложной функции

Пусть 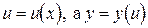. Тогда функция 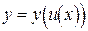будет сложной функцией от x.

Если функция 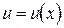дифференцируема в точке x, а функция 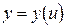дифференцируема в точке u, то 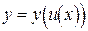тоже дифференцируема в точке x, причем

.

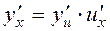Примеры.

1.

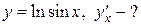
Полагаем 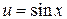, тогда 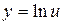. Следовательно

.

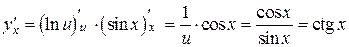При достаточном навыке промежуточную переменную u не пишут, вводя ее лишь мысленно.

2.

.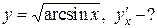
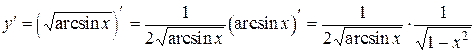