Непрерывность функции, точки разрыва и их классификация

Для рассмотренной ранее функции пределы слева и справа в точке 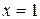не совпадают, и в таком случае говорят, что функция имеет при 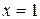разрыв.

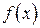Точка называется точкой разрыва первого рода, если в этой точке функция имеет конечные, но не равные друг другу правый и левый пределы.

Если хотя бы один из односторонних пределов в точке равен 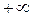или 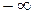, или не существует, то в данной точке функция терпит разрыв второго рода.

Точка называется точкой устранимого разрыва функции 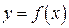, если при x ® a существуют и равны между собой односторонние пределы, но в точке функция либо не определена, либо имеет значение 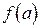, отличное от значений односторонних пределов в этой точке.

Функция 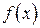называется непрерывной в точке , если функция имеет в точке одинаковые односторонние пределы, которые равны значению 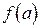функции 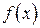в точке .

Если функция непрерывна в каждой точке некоторого промежутка, то говорят, что она непрерывна на этом (открытом) промежутке.

Функция называется непрерывной на закрытом промежутке 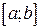, если она непрерывна в каждой внутренней точке этого промежутка и, кроме того, имеет предел справа в точке a и предел слева в точке b.

Свойства функций, имеющих предел, понятие о неопределенностях

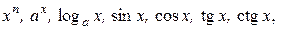
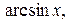
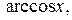
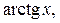
Вычислить предел функции, изучая поведение последовательности значений аргумента и функции, довольно легко для основных функций, таких, как 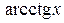в их области определения. Вычисления показывают, что в области определения предельное значение функции равно ее значению при предельном значении аргумента:

.

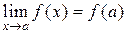В тех случаях, когда функция имеет сложный вид, т.е. составлена из нескольких других основных функций при помощи конечного числа алгебраических операций, вычисление значений функции может быть весьма утомительным и установление ее предела непосредственно затруднительным. При нахождении предела таких функций пользуются свойствами пределов функций. Сформулируем их без доказательства.

1) Предел постоянной равен самой постоянной.

2) Постоянный множитель можно выносить за знак предела.

3) Пусть функции 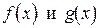имеют в точке конечные пределы, соответственно равные 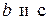. Тогда функции

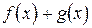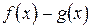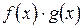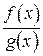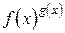имеют в точке пределы, соответственно равные

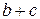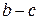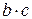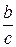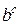В тех случаях, когда либо 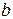, либо 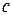, либо оба вместе равны 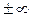, или в частном 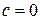, применение указанных правил не дает возможности найти предел составной функции. Рассмотрим пример. Пусть

.

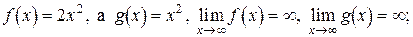
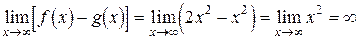Возьмем теперь

.

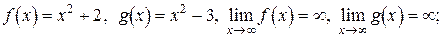
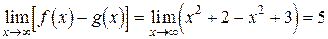Рассмотрим и такой вид функций:

,

.

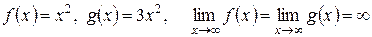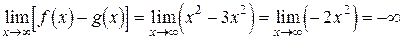Предел разности двух стремящихся к 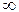функций, значение которого зависит от конкретного вида функций, называется неопределенностью вида .

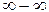Предел частного двух функций, стремящихся к нулю, значение которого зависит от конкретного вида функций, называется неопределенностью вида .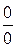

Аналогично определяются и другие неопределенности:

.
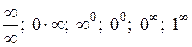