Раздел 3. Контрольная работа по математике №3

Введение в математический анализ

Теоретический материал

Основы теории пределов функций

Понятие предела функции

Независимая переменная величина , входящая в понятие функции, может, в соответствии с условиями конкретной задачи, изменяться различным образом. Например, пусть принимает такую последовательность значений:

Видно, что с увеличением номера значение приближается к 3, что кратко обозначают ( стремится к 3). Если приближается к некоторому числу со стороны меньших значений (как в приведенном примере), то говорят, что стремится к слева и обозначают: ; если же приближается к со стороны больших значений, то говорят, что стремится к справа и обозначают: . Например, запись означает, что может, в частности, принимать такую последовательность значений: 3,1; 3,01; 3,001; ...

Если в своем изменении независимая переменная может стать больше любого наперед заданного положительного числа, то это обозначают так: ( стремится к бесконечности). Если при изменении независимой переменной она может стать меньше любого наперед заданного отрицательного числа (как угодно большого по модулю), то это обозначают так: ( стремится к минус бесконечности).

Ясно, что при изменении аргумента связанная с ним функция 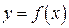будет также принимать соответствующий ряд значений. Рассмотрим, например, функцию . Одновременное изменение и аргумента и функции удобно представить таблицей:

x
f(x)		1,2	1,02	1,002

Из таблицы видно, что при неограниченном увеличении значения функции приближаются к 1.

Число 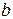называется пределом (или предельным значением) функци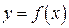и при , если для любой последовательности значений аргумента , стремящейся к , соответствующая последовательность значений функции стремится к .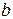

Для обозначения предела используют следующую символику:

(lim – начало латинского слова limit – предел).

Функция 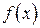называется бесконечно малой при , если ее предел при равен 0.

Например, рассмотрим функцию . Составим таблицу

		0,01	0,0001

Можно заключить, что .

В общем случае .

Функция называется бесконечно большой при , если с приближением к , модуль значения функции становится больше любого наперед заданного положительного числа.

Символически такое поведение функции описывают так:

.

В формулировке понятия предела предполагалось, что может быть и конечным числом и 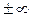. Если рассматривать только конечные значения , то можно ввести понятие одностороннего предела.

Число 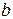называется правым пределом функции 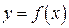в точке , если для любой последовательности значений аргумента, сходящейся к и состоящей из чисел, больших , соответствующая последовательность значений функции сходится к .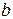

Число 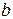называется левым пределом функции 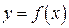в точке , если для любой последовательности значений аргумента, сходящейся к и состоящей из чисел, меньших , соответствующая последовательность значений функции сходится к .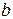

Рассмотрим функцию , найдем ее односторонние пределы в точке 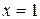. Для предела слева составим таблицу:

x		0,5	0,9

Значения функции, представленные в таблице, позволяют заключить, что .

Для предела справа составим такую таблицу:

x		1.5	1.1

Из данных этой таблицы можно сделать вывод: .