Комплексные числа и действия с ними

Под комплексным числом в алгебраической форме записи понимается выражение 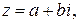где и 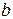– действительные числа, а 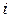– мнимая единица, для которой справедлива формула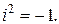

Числа вида 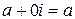отождествляются с действительными числами, числа вида 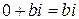называются чисто мнимыми. Сопряженным числом 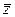к числу 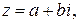называется комплексное число 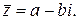Два комплексных числа 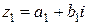и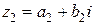равны, есл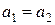и и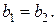

Сложение, вычитание, умножение и деление комплексных чисел определяются следующим образом.

1)

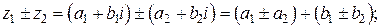
2)

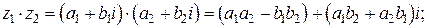
3)

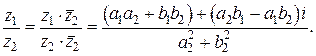
Примечание. Формулу умножения двух комплексных чисел не обязательно запоминать, так как она получается, если формально перемножить двучлены 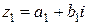и 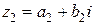по обычному правилу умножения двучленов и затем заменить 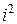на –1.

Примеры.

1. Найти сумму и произведение комплексных чисел 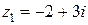и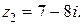

Находим сумму: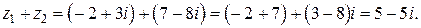

Умножим: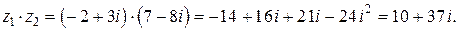

2. Найти частное комплексных чисел 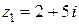и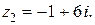

Для нахождения частного умножим числитель и знаменатель дроби на число, сопряженное знаменателю:

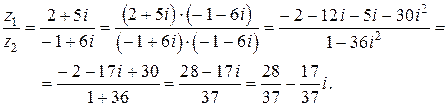
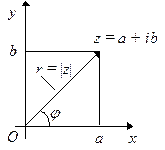Комплексное число 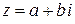можно изобразить точкой на плоскости 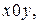имеющей координаты 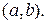На оси 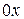изображаются действительные числа, поэтому она называется действительной осью; на оси 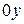расположены чисто мнимые числа; она называется мнимой осью.

Можно также сопоставить числу 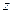вектор, направленный из начала координат в точку 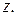Длина этого вектора 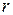, т.е. расстояние от начала координат до точки 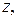называется модулем комплексного числа 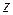и обозначается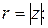

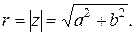
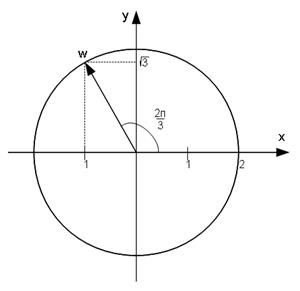
Из рисунка находим 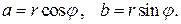Следовательно:

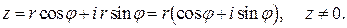
Такая форма записи комплексного числа называется тригонометрической. Угол 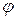, образованный радиус-вектором 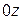с положительным направлением действительной оси 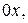называется аргументом комплексного числа 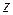и обозначается 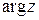. В инженерных приложениях угол 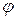также называется фазой. Величина угла 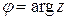определяется с точностью до слагаемого 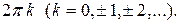Главным называется значение 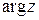, удовлетворяющее условию: .

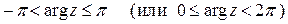Главное значение можно вычислить по следующим формулам:

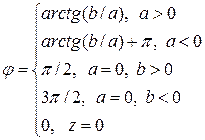
Пусть 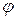– любое действительное число. Символом 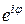обозначается комплексное число 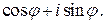С помощью этого обозначения всякое комплексное число 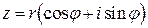может быть записано в показательной форме (формула Эйлера):

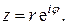
Пример. Представить в тригонометрической и показательной форме комплексное число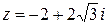

Находим модуль 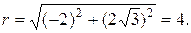Аргумент находим по формуле:

.

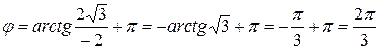Следовательно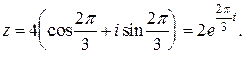

Пример решения работы

Задание №6. Решить матричное уравнение, сделать проверку.

.

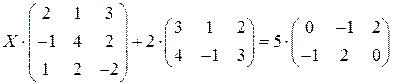Решение

Запишем данное уравнение в матричной форме:

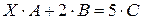, где

; ; .

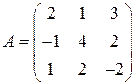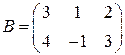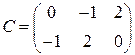Преобразуем уравнение к виду 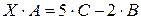и выполним действия с матрицами в правой части:

.

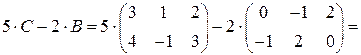
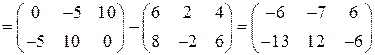Обозначим полученную матрицу 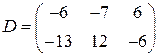и запишем уравнение в виде 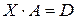. Умножив обе части последнего равенства на 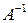справа, получим:

.

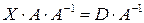Имея в виду, что 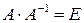, решением данного уравнения будет 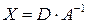, где 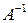− матрица, обратная матрице .

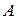Найдём обратную матрицу так, как описано в разделе 2.1.1. на стр. 15, тогда

.

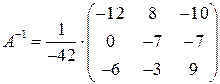Найдем решение данного уравнения, умножив матрицу 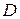на матрицу 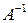. Напомним, что одну матрицу на другую можно умножать тогда и только тогда, когда число столбцов первой матрицы равно числу строк второй. В нашем случае матрица 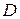имеет размер 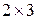, а матрица 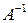− 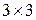, значит, произведение 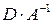имеет смысл (3=3), причем, при умножении получится матрица размера .

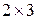По правилу умножения получим:

.

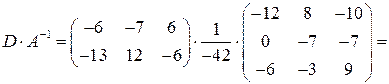
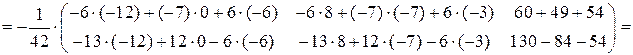
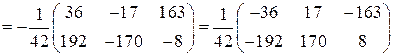Итак, .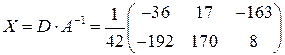

Проверим найденное решение, подставив его в исходное уравнение:

.

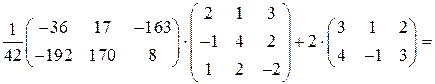
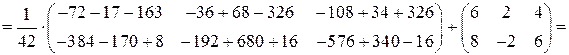
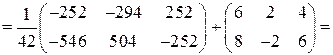
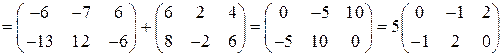Так как найденное решение 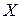обращает уравнение в тождество, то решение найдено верно.

Ответ: .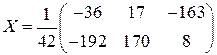

Задание №7. Дана функция 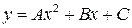, график которой проходит через три заданные точки 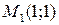, , 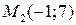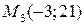. Найти параметры 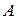, , 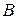, 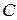решив получившуюся систему методом Гаусса, построить график функции .

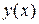Решение

Подставим координаты заданных точек в уравнение :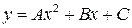

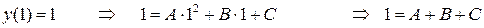
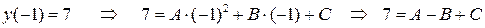
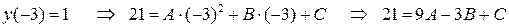
Получим систему трех линейных уравнений с тремя неизвестными для нахождения коэффициентов , , :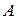

.

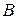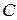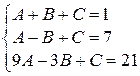Решим систему методом Гаусса. Запишем расширенную матрицу системы:

.

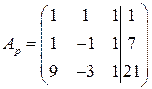Выполним над этой матрицей необходимые элементарные преобразования. Обнулим все элементы первого столбца, кроме первого элемента. Для этого умножим последовательно первую строку на 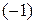, и на 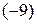и прибавим ее ко второй и третьей строке соответственно:

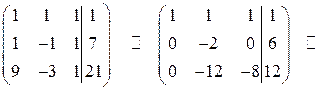
Разделим все элементы второй строки на 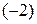, а третьей − на :

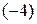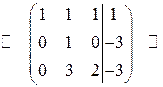
Обнулим третий элемент второго столбца. Для этого вторую строчку умножим на 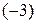и прибавим к третьей:

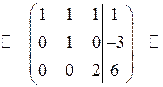
Разделим третью строчку на 2:

.

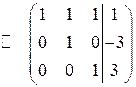Матрица приведена к ступенчатому виду. Этой матрице, которая эквивалентна матрице 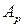, соответствует следующая система, равносильная данной:

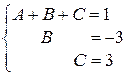
Прямой ход метода Гаусса закончен. В результате обратного хода получим:

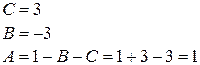
Таким образом, получаем решение системы: .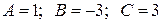

Сделаем проверку:

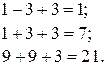
Так как все уравнения системы обратились в тождества, то решение верное.

Но тогда

.

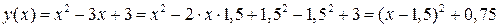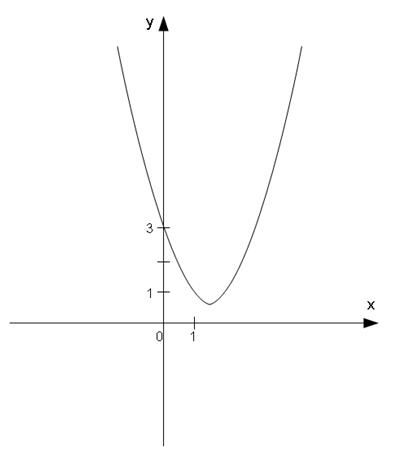
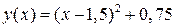− уравнение параболы с вершиной в точке 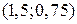, которая проходит через три данные точки 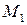, , 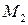, 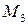пересекает ось 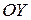в точке 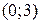, ось 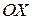не пересекает, так как уравнение 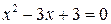не имеет действительных корней.

Построим график функции .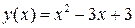

Задание №8. Решить систему уравнений по формулам Крамера:

.

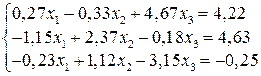Решение

Вычислим главный определитель системы:

.

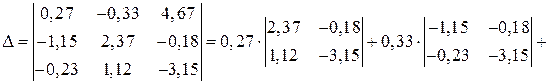
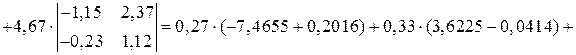
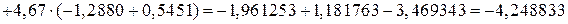Так как 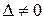, то данная система имеет единственное решение, которое найдем по формулам Крамера:

; ; .

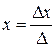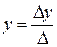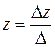Вычислим вспомогательные определители:

.

.

.

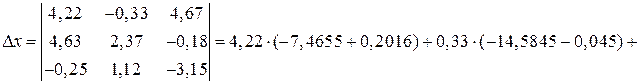
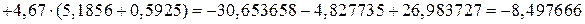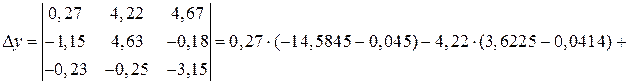
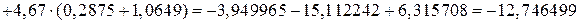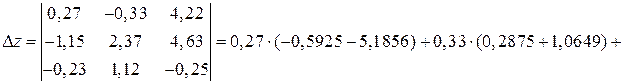
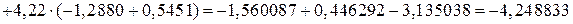Но тогда

; ; .

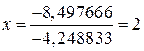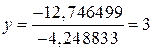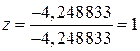Ответ: ; ; .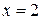

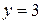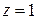Задание №9. Решить уравнение 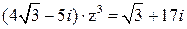. Ответ представить в тригонометрической форме. Модуль вычислить с точностью до 0,01, а аргумент в градусах. Изобразить полученные числа на комплексной плоскости.

Решение

Очевидно, что из .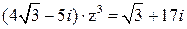

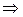
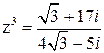Чтобы выполнить деление комплексных чисел, умножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на 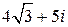, получим:

.

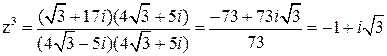Итак, 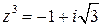. Очевидно, чтобы решить это уравнение надо найти все значения 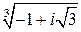. Обозначим .

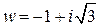Известно, что корень n−й степени из комплексного числа 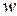имеет n различных значений, которые находятся по формуле:

,

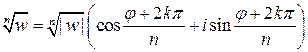где ; .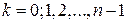

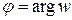Найдём тригонометрическую форму комплексного числа 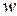как описано в разделе 2.1.3.: ;

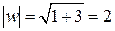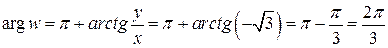
Тогда число 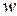в тригонометрической форме для нашего примера будет иметь вид:

.

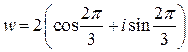Но тогда .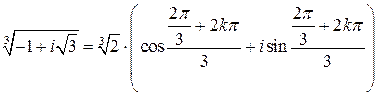

Полагая 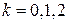, найдем

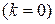
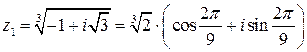
или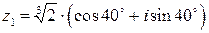

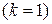
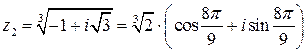
или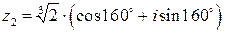

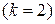
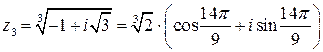
или .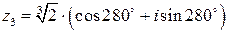

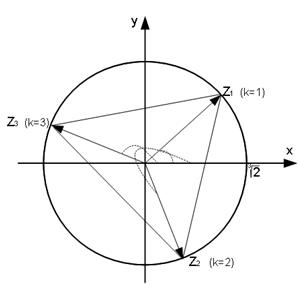Изобразим полученные числа , 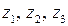на комплексной плоскости.