Раздел 1. Контрольная работа по математике №1

Введение

Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «эксплуатация транспортно-технологических машин и комплексов» и профилю «автомобили и автомобильное хозяйство», в освоении тех разделов математики, которые изучаются в первом семестре, а также помочь в выполнении контрольных работ по математике по соответствующим темам: № 1,2, 3.

В пособии имеется необходимый теоретический материал, пример выполнения соответствующей контрольной работы и задания для самостоятельного выполнения в десяти вариантах. Номер варианта определяется по последней цифре зачётной книжки (шифра).

Работу следует выполнять в тонкой ученической тетради в клетку. Выполненную работу следует снабдить титульным листом, образец которого можно найти на доске объявлений у деканата.

Поскольку пособие содержит достаточно большой теоретический материал, полезно сохранить его до конца обучения в вузе, так как он может быть востребован при дальнейшем изучении математики и других дисциплин.

Раздел 1. Контрольная работа по математике №1

Элементы векторной алгебры и аналитической геометрии

Теоретический материал для данной контрольной работы был представлен на установочных занятиях. При возникновении каких-либо вопросов следует обращаться к нему.

Пример решения работы

Задание №1. Даны два вектора и . Найти их длины , , сумму , линейную комбинацию , скалярное произведение , векторное произведение , угол (в градусах) между векторами .

Решение

1) Длины векторов равны:

; .

2) Найдем сумму и линейную комбинацию :

;

.

3) Скалярное произведение равно:

.

4) Векторное произведение равно:

.

5) Из определения скалярного произведения:

.

В условиях данной задачи:

.

Тогда .

Ответ: 1) ;

2) ; .

3) ;

4) ;

5) .

Задание №2. Найти объем, площадь основания и высоту пирамиды с вершинами в точках , , , , опущенную из вершины на грань .

Решение

Из формулы выразим высоту .

Для решения задачи введем векторы: , , , при этом , , .

1) Объем пирамиды находится как модуль смешанного произведения векторов , , :

.

2) Площадь основания находится по формуле:

,

,

3) Длина высоты, опущенной из вершины на грань , находится из формулы . Получим:

.

Ответ: ; ; .

Задание №3. Даны вершины треугольника : , , . Найти:

а) уравнение стороны ;

б) уравнение высоты ;

в) уравнение медианы ;

г) точку пересечения медианы и высоты ;

д) уравнение прямой, проходящей через вершину , параллельно ;

е) расстояние от точки 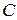до прямой ;

ж) сделать чертеж.

Для разбора решения задачи отметим на координатной плоскости точки: , , .

Решение

а) Для нахождения уравнения стороны воспользуемся уравнением прямой, проходящей через две заданные точки:

:


( ).

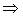
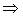
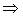
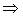
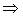
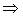
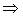
б) Для составления уравнения высоты воспользуемся условием перпендикулярности прямых и ( ), а также уравнением прямой, проходящей через данную точку с данным угловым коэффициентом:

.

Итак, : ,

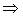
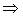
следовательно, . Тогда по условию

.

Уравнение примет вид:

: ( ).

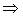
в) Для составления уравнения медианы найдем сначала координаты точки - середины отрезка :

; ; .

Тогда : ( ).

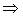
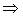
г) Для нахождения координат точки - пересечения медианы и высоты составим и решим систему уравнений:

; .

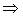
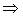
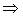
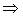
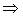
Итак, .

д) Уравнение прямой , проходящей через точку 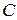параллельно , будем искать в виде: .

Так как , то (угловые коэффициенты у параллельных прямых равны).

(смотри пункт б)). Но тогда .

Итак, или .

е) Расстояние от точки 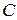до прямой может быть найдено по формуле:

, при этом, : , а, значит

; ; ; ; .

Следовательно, .

Ответ: а) ( ); б) ( ); в) ( ); г) ; д) ; е) .

Задание №4. Найти угол (в градусах) между плоскостями и .

Решение

Величина угла между плоскостями, заданными уравнениями

и

вычисляется на основании формулы:

.

А, значит, в условиях данной задачи, когда ; ; ; ; ; , имеем:

.

Итак, .

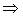
Ответ: .

Задание №5. Найти точку пересечения прямой и плоскости .

Решение

Для того, чтобы найти точку пересечения прямой и плоскости нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой в пространстве.

Параметрические уравнения данной прямой имеют вид: .

Подставив в уравнение плоскости найдем - то значение параметра, при котором происходит пересечение:

;

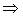
А, значит, ; ; .

Итак, точка пересечения данной прямой и данной плоскости - .

Ответ: .

Элементы линейной алгебры

Теоретический материал

Матрицы и действия с ними

Матрица представляет собой прямоугольный массив чисел, образующих строки и столбцы одинаковой длины.

Для краткого обозначения матриц применяются латинские буквы A, B, C и т.д. Если в матрице m строк и n столбцов, то говорят, что матрица имеет размер 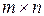. В общем виде элементы матрицы принято обозначать латинскими буквами a, b, c и т.д. Элемент, стоящий в i-той строке (т.е. в строке с номером i) и j-том столбце (т.е. столбце с номером j), обозначается и т.д. Учитывая введенные обозначения, произвольная матрица А может быть записана так:

.

Кроме больших круглых скобок, массив чисел, образующих матрицу может быть заключен в большие квадратные скобки или ограничен сдвоенными чертами. Многоточие в записи означает, что за элементом следуют элементы и т.д. до ; за элементом следуют элементы и т.д. до элемента . Элементами матрицы могут быть любые действительные и комплексные числа.

Если в матрице число строк и столбцов совпадает, т.е. , то матрица называется квадратной, а число 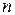указывает порядок матрицы.

Направление из левого верхнего в правый нижний угол квадратной матрицы называется главной диагональю, а элементы — диагональными элементами. Их сумма , кратко обозначаемая , называется следом матрицы . Направление, перпендикулярное главной диагонали, называется побочной диагональю.

Если в квадратной матрице все элементы, стоящие выше или ниже одной из диагоналей, равны 0, например,

то такие матрицы называются треугольными.

Если равны 0 все элементы, кроме стоящих на главной диагонали, то такая матрица называется диагональной:

.

Если все диагональные элементы равны 1, то такая матрица называется единичной:

.

Матрица, не обязательно квадратная, все элементы которой равны 0, называется нулевой.

Матрица, состоящая из одного столбца, называется матрицей-столбцом, матрица, состоящая из одной строки, называется матрицей-строкой.

Две матрицы называются равными, если они одного размера и все соответствующие элементы совпадают.

Под нормой матрицы А понимается действительное число , аналогичное понятию модуля для действительных чисел. Из элементов матрицы А ее норму можно составить различными способами, в дальнейшем за норму будем принимать корень квадратный из суммы квадратов всех элементов матрицы:

Умножение матриц

Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:

.

Т.е. элемент матрицы С, стоящий в 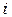-той строке и 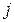-том столбце, равен сумме произведений соответствующих элементов 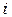-той строки матрицы А и 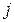-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).

Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера 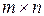на матрицу В размера дает матрицу С размера .

Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.

Пример.

.

.

Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 2, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:

;

;

.

Свойства умножения матриц

1) В общем случае , т.е. в общем случае перестановочное свойство умножения не выполняется.

Матрицы, для которых оно выполняется, называются перестановочными.

2) Сочетательное свойство: .

3) Распределительное свойство умножения относительно сложения:

4) Умножение на единичную матрицу не меняет матрицы: .

5) Умножение на нулевую матрицу дает нулевую матрицу: ;

замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что либо одна из них, либо обе вместе равны 0.

Матричные уравнения

Используя различные действия с матрицами, можно составлять матричные уравнения — соотношения между неизвестной матрицей Х и известными матрицами.

Например, АХ = В или ХА = В, АХВ = С, АХ + В = С, ХА — В = С и т.д.

Рассмотрим одно из простейших матричных уравнений:

.

В школьном курсе алгебры рассматривалось соответствующее ему уравнение для действительных чисел:

Решением этого линейного уравнения является , где число называется обратным к 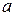и удовлетворяет соотношению: .

Введем подобное понятие и для матриц. Матрица называется обратной к , если она удовлетворяет условию:

,

где — единичная матрица.

Из определения обратной матрицы следует, что ее можно найти только для квадратных матриц.

Существование обратной матрицы дает возможность решать матричные уравнения, например, рассмотрим уравнение . Умножим обе части уравнения слева на матрицу, обратную :

.

Аналогично можно найти решение уравнения , умножая теперь уже справа обе части уравнения на :

.

Метод Гаусса

Этот метод является продолжением и обобщением рассматриваемых школе методов подстановки и сложения.

Запишем систему так, чтобы в первом уравнении при первом неизвестном коэффициент был равен 1. Если в системе есть подходящее уравнение, его можно переставить на первое место, если такого уравнения нет, то обе части первого уравнения можно разделить на коэффициент при первом неизвестном (полагая, конечно, что он отличен от 0). Умножая последовательно первое уравнение на числа, противоположные коэффициентам при первом неизвестном в остальных уравнениях, прибавляем его ко второму, третьему и т.д. уравнениям системы.

После этого во всех уравнениях системы, кроме первого, первое неизвестное будет исключено, т.е. эти уравнения будут содержать на одно неизвестное меньше, да и самих уравнений будет на одно меньше (первое не рассматриваем). Значит, эти уравнения образуют систему уравнений на порядок меньше, чем в исходной. С этой системой можно провести такие же преобразования, как на первом этапе и т.д. до тех пор, пока в одном уравнении не останется одно неизвестное. Рассмотрим примеры.

Пример 1. Решить систему линейных уравнений

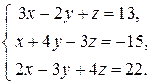
Поменяем местами первое и второе уравнения системы:

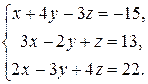
Выполним такие преобразования: ко второму уравнению системы прибавим первое, умноженное на (-3), к третьему – первое, умноженное на (-2). После выполнения указанных действий система примет вид:

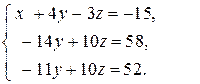
Умножив второе уравнение на (-1), прибавим его к третьему, тогда:

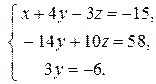
Из последнего уравнения находим 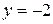, из второго 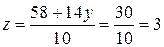; из первого 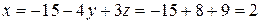. Подстановкой найденных значений во все уравнения исходной системы убеждаемся, что они являются ее решением.

Пример 2. Решить систему линейных уравнений

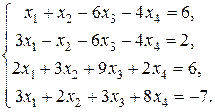
Умножая первое уравнение на (-3) и прибавляя ко второму, затем на (-2) и прибавляя к третьему, затем на (-3) и прибавляя к четвертому, преобразуем систему.

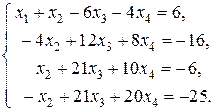
Предварительно разделив обе части второго уравнения на (-4), прибавим его к четвертому уравнению, умножив на (-1), прибавим к третьему, тогда:

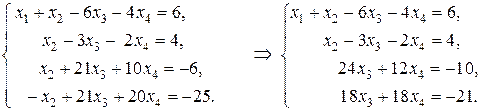
Разделим обе части третьего уравнения на 12, а четвертого - на 3, затем третье уравнение, умноженное на (-3), прибавим к четвертому, получим:

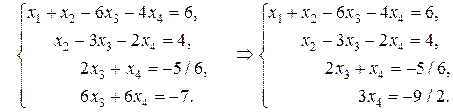
Из последнего уравнения находим 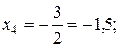из третьего 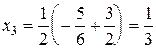; из второго 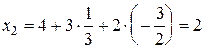; из первого 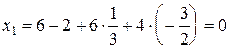. Подставляем найденные значения во все уравнения системы и убеждаемся, что решение верно.

Решение систем линейных уравнений по методу Гаусса особенно удобно, когда коэффициенты при неизвестных целые числа, в тех случаях, когда коэффициенты произвольны или даны в общем виде, решение системы (особенно вручную) по методу Гаусса может представлять непростую задачу. Попробуем найти еще один способ решения систем линейных уравнений.

Пример решения работы

Задание №6. Решить матричное уравнение, сделать проверку.

.

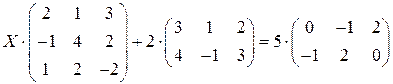Решение

Запишем данное уравнение в матричной форме:

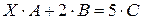, где

; ; .

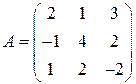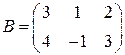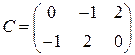Преобразуем уравнение к виду 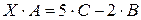и выполним действия с матрицами в правой части:

.

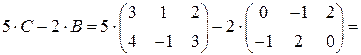
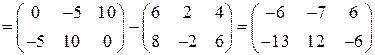Обозначим полученную матрицу 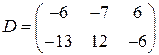и запишем уравнение в виде 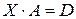. Умножив обе части последнего равенства на 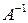справа, получим:

.

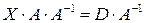Имея в виду, что 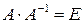, решением данного уравнения будет 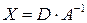, где 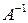− матрица, обратная матрице .

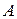Найдём обратную матрицу так, как описано в разделе 2.1.1. на стр. 15, тогда

.

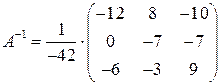Найдем решение данного уравнения, умножив матрицу 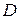на матрицу 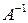. Напомним, что одну матрицу на другую можно умножать тогда и только тогда, когда число столбцов первой матрицы равно числу строк второй. В нашем случае матрица 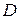имеет размер 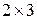, а матрица 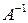− 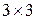, значит, произведение 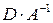имеет смысл (3=3), причем, при умножении получится матрица размера .

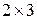По правилу умножения получим:

.

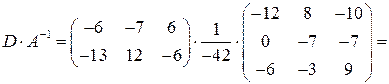
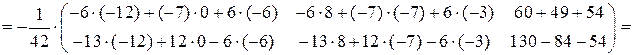
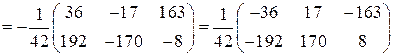Итак, .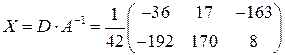

Проверим найденное решение, подставив его в исходное уравнение:

.

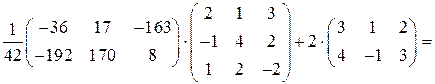
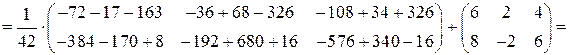
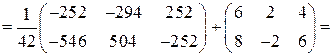
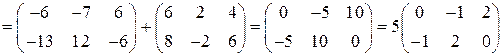Так как найденное решение 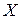обращает уравнение в тождество, то решение найдено верно.

Ответ: .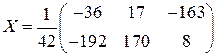

Задание №7. Дана функция 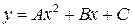, график которой проходит через три заданные точки 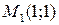, , 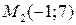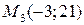. Найти параметры 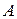, , 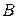, 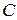решив получившуюся систему методом Гаусса, построить график функции .

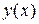Решение

Подставим координаты заданных точек в уравнение :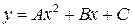

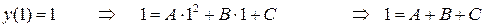
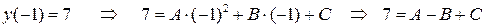
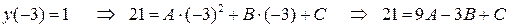
Получим систему трех линейных уравнений с тремя неизвестными для нахождения коэффициентов , , :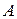

.

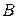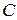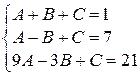Решим систему методом Гаусса. Запишем расширенную матрицу системы:

.

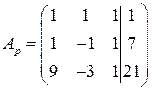Выполним над этой матрицей необходимые элементарные преобразования. Обнулим все элементы первого столбца, кроме первого элемента. Для этого умножим последовательно первую строку на 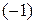, и на 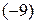и прибавим ее ко второй и третьей строке соответственно:

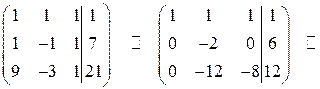
Разделим все элементы второй строки на 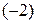, а третьей − на :

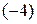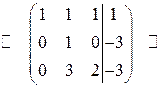
Обнулим третий элемент второго столбца. Для этого вторую строчку умножим на 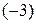и прибавим к третьей:

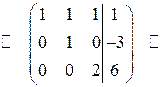
Разделим третью строчку на 2:

.

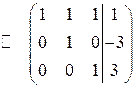Матрица приведена к ступенчатому виду. Этой матрице, которая эквивалентна матрице 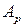, соответствует следующая система, равносильная данной:

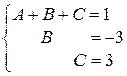
Прямой ход метода Гаусса закончен. В результате обратного хода получим:

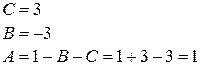
Таким образом, получаем решение системы: .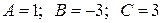

Сделаем проверку:

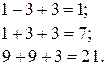
Так как все уравнения системы обратились в тождества, то решение верное.

Но тогда

.

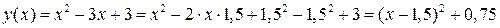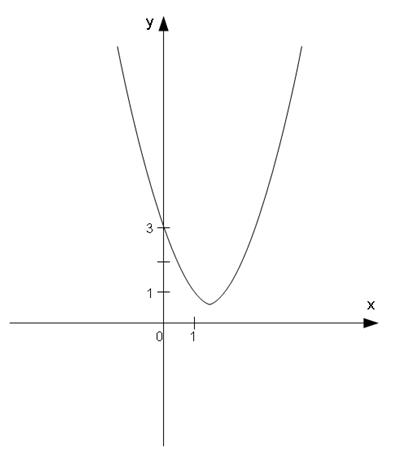
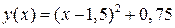− уравнение параболы с вершиной в точке 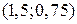, которая проходит через три данные точки , , , 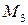пересекает ось 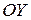в точке 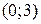, ось 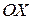не пересекает, так как уравнение 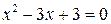не имеет действительных корней.

Построим график функции .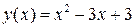

Задание №8. Решить систему уравнений по формулам Крамера:

.

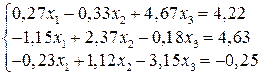Решение

Вычислим главный определитель системы:

.

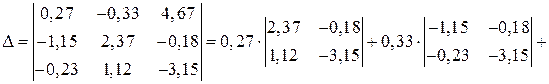
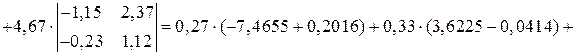
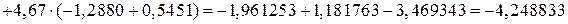Так как 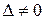, то данная система имеет единственное решение, которое найдем по формулам Крамера:

; ; .

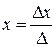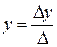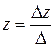Вычислим вспомогательные определители:

.

.

.

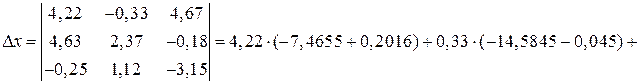
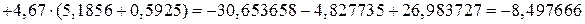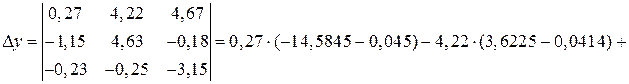
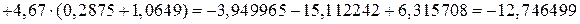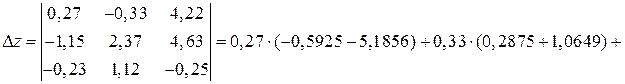
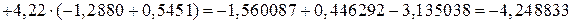Но тогда

; ; .

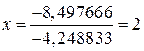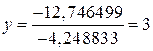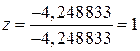Ответ: ; ; .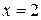

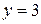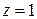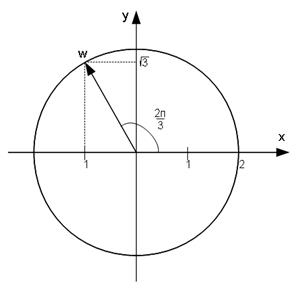
Задание №9. Решить уравнение 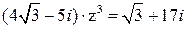. Ответ представить в тригонометрической форме. Модуль вычислить с точностью до 0,01, а аргумент в градусах. Изобразить полученные числа на комплексной плоскости.

Решение

Очевидно, что из .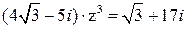

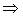
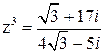Чтобы выполнить деление комплексных чисел, умножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на 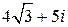, получим:

.

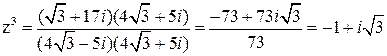Итак, 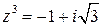. Очевидно, чтобы решить это уравнение надо найти все значения 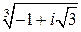. Обозначим .

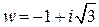Известно, что корень n−й степени из комплексного числа 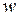имеет n различных значений, которые находятся по формуле:

,

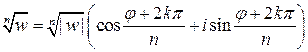где ; .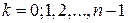

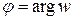Найдём тригонометрическую форму комплексного числа 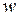как описано в разделе 2.1.3.: ;

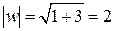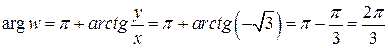
Тогда число 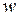в тригонометрической форме для нашего примера будет иметь вид:

.

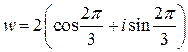Но тогда .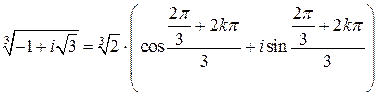

Полагая , найдем

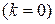
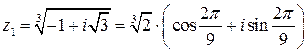
или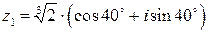

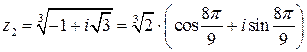
или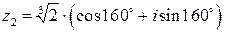

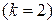
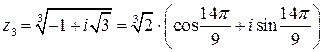
или 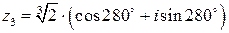.