Оценка параметров классической регрессионной модели методом наименьших квадратов.

Данные, используемые в корреляционно-регрессионном анализе, рассматриваются как выборочные, неполные. Поэтому количественные характеристики связи между показателями, полученные на основе этих данных, также являются выборочными, т. е. содержащими некую ошибку, отличающимися от объективно существующих, но неизвестных «подлинных» характеристик.

Параметры уравнения регрессии, найденные на основе имеющихся у исследователя данных, называют оценками параметров, подчеркивая то, что они рассчитаны по выборочным данным. Оценки параметров могут меняться от выборки к выборке, поэтому они рассматриваются как случайные величины.

Так как найденные параметры являются лишь выборочными оценками неизвестных параметров по генеральной совокупности, то возникает вопрос об их качестве. Считается, что оценками параметров можно пользоваться для дальнейшего анализа и прогноза, если эти оценки являются несмещенными, эффективными и состоятельными.

Оценка параметра является несмещенной, если её математическое ожидание равно оцениваемому параметру или математическое ожидание остатков равно нулю.

Оценка параметра является эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок данного параметра по выборкам одного и того же объема.

Оценка параметра является состоятельной, если с увеличением числа наблюдений оценка параметра стремится к его значению в генеральной совокупности, т.е. точность оценок выборки увеличивается с увеличением объема выборки.

Наиболее простым методом, применяющимся для оценки параметров множественной регрессии, является метод наименьших, квадратов (МНК).

Для оценки вектора неизвестных параметров 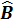применим метод наименьших квадратов. Как и в случае регрессионного уравнения с одной переменной целью метода является выбор вектора оценок 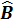, минимизирующего сумму квадратов остатков E_i (т.е. квадрат длины вектора остатков E):

Оценка метода наименьших квадратов:

(4)

Теорема Гаусса-Маркова.

Предположим, что:

1. Y=XB+E;

2. X – детерминированная матрица, имеет максимальный ранг k+1

3. М(ε)=0; V(ε)=М(εε^T)=σ²I_n.

Тогда оценка метода наименьших квадратов 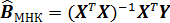является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных (по y) несмещенных оценок.

1.3 Анализ вариации зависимой переменной в регрессии. Коэффициенты R2 и скорректированный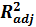

Для регрессионной модели известны следующие величины дисперсий:

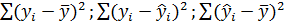где 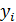– значение зависимой переменной по исходным данным, 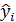- значение зависимой переменной, вычисленное по регрессионной модели, 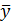- среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство

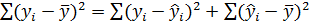
Как и в случае регрессионной модели с одной независимой переменной, вариацию 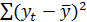можно разбить на две части: объясненную регрессионным уравнением и необъясненную ( т.е. связанную с ошибками ε).

Поэтому верно равенство

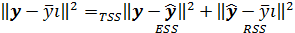(7)

Записывая (7) в отклонениях 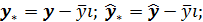получим теорему Пифагора:

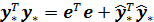(8)

Определим коэффициент детерминации 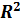как

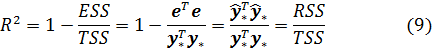
Отметим, что коэффициент R² корректно определен только в том случае, если константа, т.е. вектор 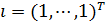, принадлежит линейной оболочке векторов 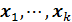. В этом случае R² принимает значения из интервала [0,1].

Коэффициент R² показывает качество подгонки регрессионной модели к наблюдаемым значениям y_t.

Если R²=0, то регрессия 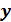на 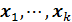не улучшает качество предсказания y_t по сравнению с тривиальным предсказанием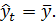

Другой крайний случай R²=1 означает точную подгонку: все e_t=0, т.е. все точки наблюдений удовлетворяют уравнению регрессии.

Пример другого обозначения: Для модели регрессии вида 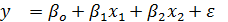, где 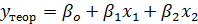, рассчитаны дисперсии 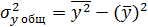, , 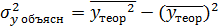, 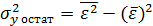тогда величина коэффициента детерминации рассчитывается по формуле 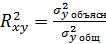или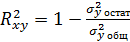

В какой степени допустимо использовать критерий R² для выбора между несколькими регрессионными уравнениями? Следующие два замечания побуждают не полагаться только на значение R².

1. R², вообще говоря, возрастает при добавлении еще одного регрессора.

2. R² изменяется даже при простейшем преобразовании зависимой переменной, поэтому сравнивать по значению R² можно только регрессии с одинаковыми зависимыми переменными.

Если взять число регрессоров равным числу наблюдений, всегда можно добиться того, что R²=1, но это вовсе не будет означать наличие содержательной (имеющей экономический смысл) зависимости у от регрессоров.

Попыткой устранить эффект, связанный с ростом R² при возрастании числа регрессоров, является коррекция R² на число регрессоров.

Скорректированным (adjusted) R² называется

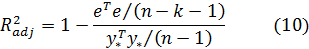
Заметим, что нет никакого существенного оправдания именно такого способа коррекции.

Свойства скорректированного R²:

1.

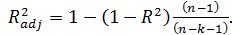
2.

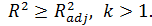
3. 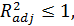но может принимать значения < 0.

В определенной степени использование скорректированного коэффициента детерминации 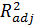, более корректно для сравнения регрессий при изменении количества регрессоров.

Скорректированный коэффициент детерминации применяется для оценки реальной тесноты связи между результатом и факторами и сравнения моделей с разным числом параметров.

В классической множественной линейной регрессии абсолютным показателем силы связи результата с фактором 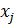является коэффициент 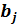при соответствующем факторе.

Коэффициенты 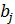линейной модели множественной регрессии называют коэффициентами условно-чистой регрессии. Они показывают на сколько единиц в среднем изменится результат при изменении фактора 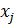на 1 при фиксированном уровне других факторов, включенных в модель.

В классической множественной линейной регрессии относительным показателем силы связи результата с фактором 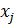является коэффициент эластичности

Коэффициенты эластичности показывают на сколько процентов в среднем изменится результат при изменении фактора 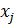на 1% и значениях других факторов, фиксированных на средних уровнях.

В множественной регрессии показателями тесноты связи являются: коэффициент множественной корреляции и коэффициент множественной детерминации.

Проверка гипотез.