Оценка значимости выборочного коэффициента парной корреляции
Для оценки значимости выборочного коэффициента парной корреляции применяется t-критерий Стьюдента. При этом фактическое значение этого критерия определяется по формуле:
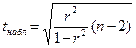, (2.2)
где n – число наблюдений. Полученное значение сравнивается с табличным критическим значением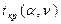 
, зависящим от уровня значимости α и числа степеней свободы 
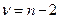. Критическое значение может быть найдено по соответствующим таблицам, а при использовании табличного процессора Excel – с помощью функции СТЬЮДРАСПОБР (α ; γ).
При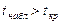 
полученное значение коэффициента корреляции r признается значимым, то есть между переменными имеется линейная корреляционная зависимость.
Для рассмотренного Примера 1 при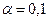 
, с учётом количества степеней свободы 
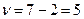критическое значение 
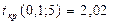. Вычислим 
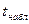для каждой пары переменных и сделаем вывод о значимости соответствующих коэффициентов корреляции.
Для пары переменных y, x1 :
.
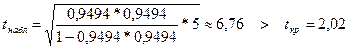Следовательно, значение коэффициента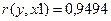 
является значимым.
Для пары переменных y, x2 :
.
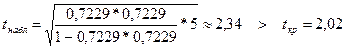Следовательно, мы можем утверждать, что значение коэффициента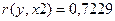 
является значимым.
Для пары переменных x1, x2 :
.
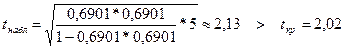Следовательно, значение коэффициента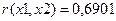 
является значимым.
Поскольку мы выбрали уровень значимости 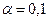, то с вероятностью 10% мы сделали ошибочные выводы, а с вероятностью 
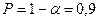наши выводы верны.
Модель парной регрессии. Основные понятия. Линейная парная регрессия
Регрессионное уравнение, разрешённое относительно исследуемой переменной у при наличии одной факторной переменной x, в общем виде записывается как:
,
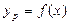и показывает, каково будет в среднем значение переменной y, если переменная х примет конкретное значение. Индекс р указывает на то, что мы получаем расчётное значение переменной y. Мы говорим в среднем, поскольку под влиянием неучтённых в модели факторов и в результате погрешностей измерения фактическое значение переменной y может принимать различные значения для одного значения x.
Если f(x) является линейной функцией, то мы имеем общий вид модели парной линейной регрессии:
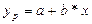, (2.3)
где a – постоянная величина (или свободный член уравнения), b – коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны наблюдения. Коэффициент регрессии характеризует изменение переменной y при изменении значения x на единицу. Если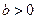 
, то переменные положительно коррелированны, если 
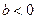- отрицательно коррелированны. Фактическое значение исследуемой переменной y тогда может быть представлено в виде:
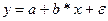, (2.4)
где ε – разность между фактическим значением (результатом наблюдения) и значением, рассчитанным по уравнению модели. Если модель адекватно описывает исследуемый процесс, то ε – независимая нормально распределённая случайная величина с нулевым математическим ожиданием (Мε = 0) и постоянной дисперсией (Dε = σ2). Наличие случайной компоненты ε отражает тот факт, что присутствуют другие факторы, влияющие на исследуемую переменную и не учтённые в модели.