Временные ряды. Авторегрессия

В табл.13 приводятся наблюдения продаж некоторого товара. Переменная t - номер наблюдения. Переменная y_t – выручка за один день.

Таблица 13

t

yt

t

yt

1.Данные таблицы представляют временной ряд. Оценим характер временного ряда визуально. Для этого построим его диаграмму, представленную на рис.3.

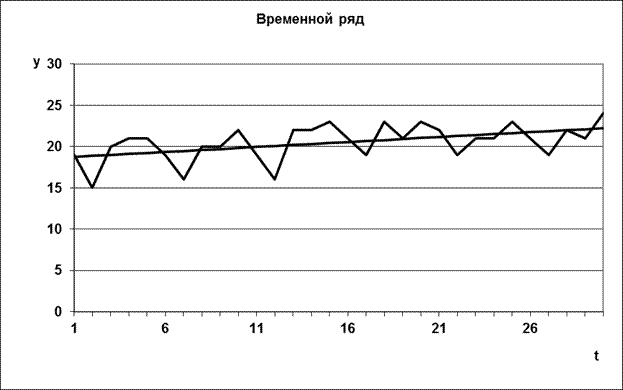
Рис.3. Временной ряд и тренд (прямая линия) продаж товара.

По графику временного ряда можно увидеть, что значения временного ряда возрастают с увеличением номера наблюдения. Это означает, что у временного ряда может быть тренд. Определим параметры тренда. Для этого построим линейную регрессионную модель с регрессором t:

.

Определим оценки параметров: 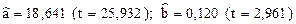(в скобках представлено отношение Стьюдента, критическое значение t_a=2,048, число степеней свободы 30-2=28). Поскольку 2,961>2,048, оценка параметраb является значимой и тренд у временного ряда существует.

Таблица 14
t	yt	et	t-5		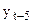t*	y*t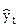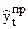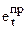
Н а б л ю д е н и я			0,239					19,676
		-3,881					19,749
		0,999					19,822
		1,879					19,895
		1,759					19,968
		-0,361			5,323	6,137	20,041	19,583	-0,583
		-3,481			5,646	5,845	20,114	16,899	-0,899
		0,399			5,969	6,46	20,187	20,307	-0,307
		0,279			6,292	5,783	20,260	21,008	-1,008
		2,160			6,615	7,783	20,333	21,032	0,968
		-0,960			6,938	6,137	20,406	19,701	-0,701
		-4,080			7,261	5,168	20,479	17,694	-1,694
		1,800			7,584	8,46	20,552	20,425	1,575
		1,680			7,907	8,46	20,625	20,449	1,551
		2,560			8,23	8,106	20,698	21,827	1,173
		0,440			8,553	8,137	20,771	19,819	1,181
		-1,680			8,876	8,168	20,844	17,812	1,188
		2,200			9,199	8,106	20,917	21,897	1,103
		0,080			9,522	6,106	20,990	21,921	-0,921
		1,960			9,845	7,429	21,063	22,622	0,378
		0,840			10,168	7,783	21,136	21,291	0,709
		-2,279			10,491	6,137	21,209	19,961	-0,961
		-0,399			10,814	5,429	21,282	22,692	-1,692
		-0,519			11,137	6,783	21,355	21,362	-0,362
		1,361			11,46	7,429	21,428	22,739	0,261
		-0,759			11,783	6,106	21,501	22,086	-1,086
		-2,879			12,106	6,137	21,574	20,079	-1,079
		0,001			12,429	7,783	21,647	21,456	0,544
		-1,119			12,752	6,783	21,720	21,480	-0,480
		1,761			13,075	8,429	21,793	22,857	1,143
Σ			0,0	325,0	508,0	230,0	175,084	622,0	519,0	0,0
Σ/n	15,5	20,5	0,0	10,833	16,933	7,666	5,836	20,734	17,300	0,0
Прогноз								21,866	22,105
							21,939	21,452
							22,012	23,506
							22,085	17,324
							22,158	22,000

Вычислим прогнозные значения

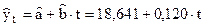
и отклонения от прогноза

.

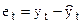Результаты расчетов представлены в табл.14. Линия тренда показана на рис.3.

Сумма квадратов отклонений остатков построенной модели ESS=103,2, общая сумма квадратов TSS=135,5. Коэффициент детерминации R²=0,239, отношение Фишера F=8,771 (критическое значение F_a=4,196). Модель тренда является значимой по критерию Фишера.

2.Исследуем возможности увеличения значимости данной модели. Для этого определим выборочную автокорреляционную функцию остатков построенной модели. Ее значения рассчитываются по формуле

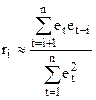
и представлены в табл.15. Гистограмма автокорреляционной функции показана на рис.4.

Таблица 15
Автокорреляционная функция
i
ri		-0,015	-0,273	-0,336	-0,04	0,677	-0,094

Рис.4. Гистограмма автокорреляционной функции.

При i=5 автокорреляция (0,677) значительно превосходит по модулю соседние значения, и указывает на корреляцию остатков через 5 наблюдений. Для продаж, которые осуществляются по рабочим дням (5 дней в неделю), характерна так называемая недельная сезонная компонента. Если фиксируются поквартальные данные, то может наблюдаться корреляция остатков при i=4 (квартальная сезонная компонента). Если рассматриваются месячные данные, то может наблюдаться значимая корреляция при i=12 и т.д.

В связи с тем, что отклонения продаж товара от тренда, коррелируют через 5 дней, предлагается следующая модель временного ряда:

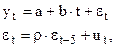
где u_t – случайные отклонения, удовлетворяющие требованиям классической ЛРМ.

Вычислим

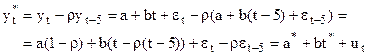
Получена классическая ЛРМ, параметры которой могут оцениваться с помощью МНК при этом оценки являются состоятельными, несмещенными и эффективными. Оценка параметра 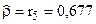. Вычислим 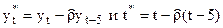и включим найденные значения в таблицу. МНК оценки параметров 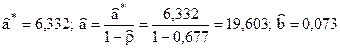. Получена ЛРМ с учетом сезонных колебаний

.

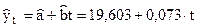Прогнозирование в этой модели осуществляется с учетом последних наблюдений временного ряда:

.

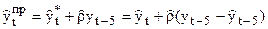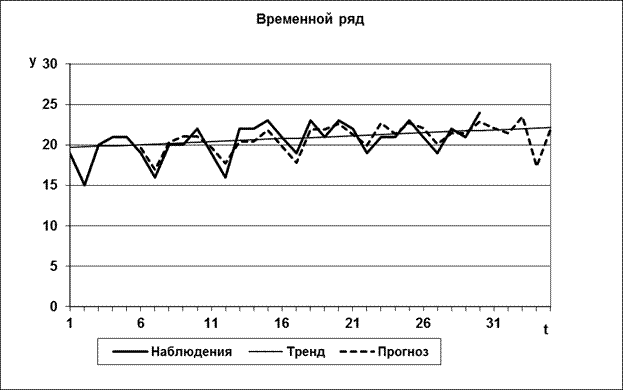
Рис.5. Временной ряд, линейный тренд и прогноз с учетом корреляции остатков.

Сумма квадратов остатков построенной модели ESS=26,5, общая сумма квадратов TSS=135,5. Коэффициент детерминации R²=0,804, отношение Фишера F=94,6 (критическое значение F_a=4,279, число степеней свободы 30-2-5=23). Значимость модели заметно улучшилась. Прогноз продаж товара на следующую рабочую неделю представлен в таблице и на рис.5.

ЛЕКЦИИ

Тема 1. Введение. Эконометрика и эконометрическое моделирование: основные понятия и определения

Эконометрика – это наука, которая даёт количественное выражение взаимосвязей экономических явлений и процессов.

Основные задачи эконометрики: построение количественно определённых экономико-математических моделей, разработка методов оценки их параметров по статистическим данным, анализ свойств построенных моделей и прогнозирование на их основе экономических процессов.

Можно выделить три основных класса моделей, которые применяются для анализа и прогнозирования экономических процессов:

- модели временных рядов,

- регрессионные модели с одним уравнением,

- системы одновременных уравнений.

При этом все переменные любой эконометрической модели по способу их вхождения в эту модель можно разбить на объясняемые (зависимые, исследуемые) переменные и объясняющие (предопределённые, факторные) переменные.

Например, если мы будем решать задачу прогнозирования продаж мороженого в определённый день каким-либо торговым предприятием, то объясняемой переменной будет объём продаж, а объясняющими переменными могут выступать: температура воздуха, торговая наценка, среднедушевой доход населения и другие.

Необходимым условием использования той или иной переменной при построении модели является наличие ряда данных наблюдений (измерений) величины этой переменной, либо получение ряда значений с использованием дополнительных вычислений на основе наблюдений о показателях, объясняющих интересующую нас переменную.

Например, определение достоверных значений среднедушевого дохода непосредственно по результатам опросов и бухгалтерской отчётности может оказаться сложнее оценки изменения дохода на основе информации об изменении розничного оборота товаров и услуг, а также изменении общей суммы банковских вкладов населения.

В эконометрике выделяют три типа данных:

I. Кросс секционные (перекрёстные) данные представляют ситуацию в группе переменных в отдельный момент времени. Таковыми, например, являются публикуемые в деловых разделах газет списки цен на различные акции, процентные ставки по разным видам вкладов и обменные курсы разных валют. Другим примером может служить информация о продажах торговым предприятием в определённый день товаров различных групп (пищевых, хозяйственных и т.д.)

II. Пространственные данные характеризуют ситуацию по конкретной переменной (или набору переменных), относящейся к пространственно разделённым однотипным объектам в один момент времени. Например, данные о курсах валют в один день по разным обменным пунктам города или продажи мороженого в различных киосках в один день.

III. Временные ряды отражают изменения (динамику) какой-либо переменной на промежутке времени. Например, данные об обменном курсе валюты за каждый день в конкретном обменном пункте или данные о продажах мороженого в одном киоске за каждый день будут являться ежедневным временным рядом.

Эконометрическое моделирование состоит из следующих этапов:

1. На постановочном этапе формулируются конечные цели моделирования, определяется наборы возможных исследуемых (объясняемых) переменных 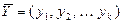и факторных (объясняющих) переменных .

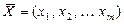2. На предварительном этапе осуществляется предварительный анализ экономической сути изучаемого явления, возможностей сбора и обработки статистических данных.

3. На этапе параметризации производится выбор общего вида модели, в том числе состава и формы входящих в неё связей. Например, может быть выбрана модель с одной объясняющей и одной объясняемой переменными – модель парной регрессии. Если объясняющих (факторных) переменных используется две или более, то говорят об использовании модели множественной регрессии. При этом, в качестве вариантов могут быть выбраны линейная, экспоненциальная, гиперболическая, показательная и другие виды функций, связывающие эти переменные.

4. Информационный этап заключается в сборе информации (проведение наблюдений, использование материалов отчётности и т.д.) и предварительном анализе данных (проверка аномальных значений показателей, сглаживание, тестирование на наличие тенденции исследуемых показателей к изменению).

5. Идентификация модели посвящена определению неизвестных параметров (коэффициентов) модели с использованием имеющегося набора данных. Наибольшее распространение для оценки параметров получил метод наименьших квадратов.

6. Проверка (верификация) модели и прогнозирование предполагает сопоставление реальных и модельных данных, проверку адекватности модели, оценку точности модельных данных. Если модель адекватна и имеет приемлемую точность, то на её основе строится прогноз – точечный и интервальный.