Положительные и отрицательные числа 6 кл.М.07

Числа со знаком + называют положительными.

Числа со знаком - называют отрицательными.

Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.

Натуральные числа, противоположные им числа и нуль называют целыми числами.

Модуль числа

Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А (а).

5 4

-5 0 4 х

а, если а ≥ 0

│а│=

-а, если а < 0

│0│=0

│4│=4

│-5│=5

Сложение и вычитание 6 кл.М.08

Положительных и отрицательных чисел

Чтобы сложить два отрицательных числа, надо:

ü Сложить их модули;

ü Поставить перед полученным числом знак - .

-8,7+ (-3,5)= - ( 8,7 + 3,5 ) = - 12,2

-2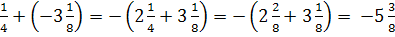

Чтобы сложить два числа с разными знаками, надо:

ü Из большего модуля слагаемых вычесть меньший;

ü Поставить перед полученным числом знак того слагаемого, модуль которого больше.

6,1 + ( -4,2 ) = + (6,1 – 4,2 ) = 1,9

- 8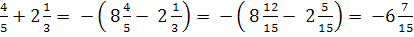

Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a-b=a+(-b)

18 – 14 =- 18 + ( - 14) = - ( 18 + 14 )= - 32

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Умножение и деление 6 кл.М.09

Положительных и отрицательных чисел

Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак - .

( - 1,2 ) · 0,3 = - ( 1,2 · 0,3 ) = - 0,36

1,2 · ( - 0,3 ) = - ( 1,2 · 0,3 ) = - 0,36

Чтобы перемножить два отрицательных числа, надо перемножить их модули.

( - 3,2 ) · ( - 9 ) = │ - 3,2 │· │ - 9 │= 3,2 · 9 = 28,8

Или ( - 3,2 ) · ( - 9 ) = 3,2 · 9 = 28,8

Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.

( - 12 ) ÷ ( - 4 ) =│-12│ ÷ │ -4│ = 3

Или ( - 12 ) ÷ ( - 4 ) =12 ÷ 4 = 3

При делении чисел с разными знаками, надо:

ü Разделить модуль делимого на модуль делителя;

ü Поставить перед полученным числом знак - .

3,6 ÷ ( - 3 ) = - ( 3,6 ÷ 3 ) = - 1,2

( -

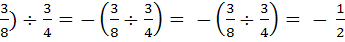
Делить на нуль нельзя!

Рациональные числа 6кл.М.10

Число, которое можно записать в виде отношения , где a- целое число, а n – натуральное число, называют рациональным числом.

Любое целое число а является рациональным числом, т.к. его можно записать в виде .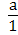

-3 = 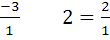0=

Сумма, разность и произведение рациональных чисел тоже рациональное число.

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Свойства действий с рациональными числами

· Переместительное свойство сложения

a + b = b + a

· Сочетательное свойство сложения

a + ( b + c ) = ( a + b ) + c

· Прибавление нуля не изменяет числа

а + 0 = а

· Сумма противоположных чисел равна нулю

а + ( - а ) = 0

· Переместительное свойство умножения

ab = ba

· Сочетательное свойство умножения

a ( b c ) = ( a b ) c

· Распределительное свойство умножения относительно сложения

( a + b ) c = ac + bc

· a · 1=a, a · 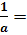1, если а≠0, а · 0 = 0

Раскрытие скобок 6 кл.М.11

Если перед скобками стоит знак + , то можно опустить скобки и этот знак +, сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком + .

a + ( b + c ) = a + b + c a + ( - b + c ) = a – b + c

Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.

- ( a + b ) = - a – b

Чтобы раскрыть скобки, перед которыми стоит знак - , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные. А потом раскрыть скобки.

Коэффициент

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом ( или просто коэффициентом)

0,3а · ( - 0,7 b) = - 0,21 ab

Подобные слагаемые

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

- 9х + 7х - 5х + 2х = ( -9 +7 -5 +2)х= - 5х

Решение уравнения

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.