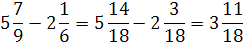Сложение и вычитание дробей 6кл.М.03

Делители и кратные 6кл.М.01

Делителем натурального числа а называется натуральное число, на которое а делится без остатка.

Кратнымнатурального числа а называют натуральное число , которое делится без остатка на а.

Любое натуральное число имеет бесконечно много кратных.

Признаки делимости

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.

Если запись натурального числа оканчивается чётной цифрой, то это число делится без остатка на 2.

Если сумма цифр числа делится на 9, то и число делится на 9.

Если сумма цифр числа делится на 3, то и число делится на 3

НОД и НОК 6кл.М.02

Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.

Натуральное число называют составным, если оно имеет более двух делителей.

Наибольшее натуральное число, на которое делятся без остатка числа a и b , называют наибольшим общим делителем этих чисел. НОД(24;36)=12

Натуральные числа называют взаимно простыми, если наибольший общий делитель равен 1.

Чтобы найти НОД нескольких натуральных чисел , надо:

ü Разложить их на простые множители;

ü Из множителей , входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

ü Найти произведение оставшихся множителей

Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.

Чтобы найти наименьшее общее кратное нескольких натуральных чисел , надо:

ü Разложить их на простые множители;

ü Выписать множители, входящие в разложение остальных чисел

ü Добавить к ним недостающие множители из разложений остальных чисел

ü Найти произведение получившихся множителей

НОД(24;36)= 2·2·3=12 НОК(24;36)=2·2·2·3·3=72

24 2 36 2 24 2 36 2

12 2 18 2 12 2 18 2

6 2 9 3 6 2 9 3

3 3 3 3 3 3 3 3

1 1 1 1

Сложение и вычитание дробей 6кл.М.03

С разными знаменателями

Чтобы сравнить(сложить, вычесть) дроби с разными знаменателями, надо:

ü Привести данные дроби к наименьшему общему знаменателю;

ü Сравнить (сложить, вычесть) полученные дроби

ü

+ -

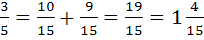
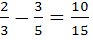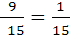
Чтобы сложить смешанные числа , надо:

ü Привести дробные части этих чисел к наименьшему общему знаменателю;

ü Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части

ü

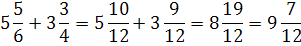
Чтобы выполнить вычитание смешанных чисел, надо:

ü Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;

ü Отдельно выполнить вычитание целых частей и отдельно дробных частей

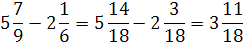
Обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.

=

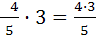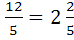
Чтобы умножить дробь на дробь, надо:

ü Найти произведение числителей и знаменателей этих дробей;

ü Первое произведение записать числителем, а второе – знаменателем.

ü

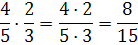
Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Чтобы найти дробь от числа , нужно умножить число на эту дробь.

Чтобы умножить смешанное число на натуральное число, можно:

ü Умножить целую часть на натуральное число

ü Умножить дробную часть на это натуральное число

ü Сложить полученные результаты

Два числа, произведение которых равно 1, называют взаимно обратными.

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

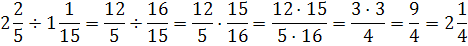
Чтобы найти число по данному значению его дроби, надо это значение разделить на эту дробь.

Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Масштаб 6 кл.М.06

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.

М=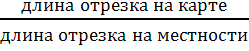

Шар

d

r

r- радиус шара

d – диаметр шара

Модуль числа

Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А (а).

5 4

-5 0 4 х

а, если а ≥ 0

│а│=

-а, если а < 0

│0│=0

│4│=4

│-5│=5

Рациональные числа 6кл.М.10

Число, которое можно записать в виде отношения , где a- целое число, а n – натуральное число, называют рациональным числом.

Любое целое число а является рациональным числом, т.к. его можно записать в виде .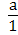

-3 = 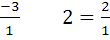0=

Сумма, разность и произведение рациональных чисел тоже рациональное число.

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Раскрытие скобок 6 кл.М.11

Если перед скобками стоит знак + , то можно опустить скобки и этот знак +, сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком + .

a + ( b + c ) = a + b + c a + ( - b + c ) = a – b + c

Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.

- ( a + b ) = - a – b

Чтобы раскрыть скобки, перед которыми стоит знак - , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные. А потом раскрыть скобки.

Коэффициент

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом ( или просто коэффициентом)

0,3а · ( - 0,7 b) = - 0,21 ab

Подобные слагаемые

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

- 9х + 7х - 5х + 2х = ( -9 +7 -5 +2)х= - 5х

Решение уравнения

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.

Параллельные прямые

Две не пересекающиеся прямые на плоскости называют параллельными.

В

А АВ │ СД

С Д

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

c a c, b c a││b

а

b

через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.

Математика

Класс

1.Делители и кратные . Признаки делимости

2. НОД и НОК

3. Сложение и вычитание дробей с разными знаменателями

4. Умножение и деление обыкновенных дробей

5. Отношения и пропорции

6. Длина окружности. Площадь круга.

7. Положительные и отрицательные числа. Модуль числа

8. Сложение и вычитание положительных и отрицательных чисел

9. Умножение и деление положительных и отрицательных чисел

10. Рациональные числа

11. Раскрытие скобок. Подобные слагаемые

12. Перпендикулярные прямые. Параллельные прямые

Делители и кратные 6кл.М.01

Делителем натурального числа а называется натуральное число, на которое а делится без остатка.

Кратнымнатурального числа а называют натуральное число , которое делится без остатка на а.

Любое натуральное число имеет бесконечно много кратных.

Признаки делимости

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.

Если запись натурального числа оканчивается чётной цифрой, то это число делится без остатка на 2.

Если сумма цифр числа делится на 9, то и число делится на 9.

Если сумма цифр числа делится на 3, то и число делится на 3

НОД и НОК 6кл.М.02

Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.

Натуральное число называют составным, если оно имеет более двух делителей.

Наибольшее натуральное число, на которое делятся без остатка числа a и b , называют наибольшим общим делителем этих чисел. НОД(24;36)=12

Натуральные числа называют взаимно простыми, если наибольший общий делитель равен 1.

Чтобы найти НОД нескольких натуральных чисел , надо:

ü Разложить их на простые множители;

ü Из множителей , входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

ü Найти произведение оставшихся множителей

Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.

Чтобы найти наименьшее общее кратное нескольких натуральных чисел , надо:

ü Разложить их на простые множители;

ü Выписать множители, входящие в разложение остальных чисел

ü Добавить к ним недостающие множители из разложений остальных чисел

ü Найти произведение получившихся множителей

НОД(24;36)= 2·2·3=12 НОК(24;36)=2·2·2·3·3=72

24 2 36 2 24 2 36 2

12 2 18 2 12 2 18 2

6 2 9 3 6 2 9 3

3 3 3 3 3 3 3 3

1 1 1 1

Сложение и вычитание дробей 6кл.М.03

С разными знаменателями

Чтобы сравнить(сложить, вычесть) дроби с разными знаменателями, надо:

ü Привести данные дроби к наименьшему общему знаменателю;

ü Сравнить (сложить, вычесть) полученные дроби

ü

+ -

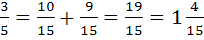
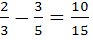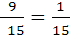
Чтобы сложить смешанные числа , надо:

ü Привести дробные части этих чисел к наименьшему общему знаменателю;

ü Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части

ü

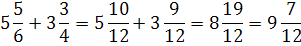
Чтобы выполнить вычитание смешанных чисел, надо:

ü Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;

ü Отдельно выполнить вычитание целых частей и отдельно дробных частей