Дифференциальные уравнения второго порядка.
Определение 8. Если дифференциальное уравнение содержит производную или дифференциал не выше второго порядка, то оно называется дифференциальным уравнением второго порядка.
Общий вид такого уравнения
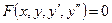 ,
,
где 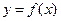 - искомая неизвестная функция,
- искомая неизвестная функция, 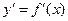 и
и 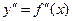 - ее производные по x первого и второго порядков, а
- ее производные по x первого и второго порядков, а 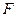 - заданная функция переменных
- заданная функция переменных 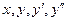 .
.
Определение 9. Общим уравнением дифференциального уравнения второго порядка называется функция 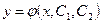 от x и двух произвольных постоянных
от x и двух произвольных постоянных 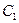 и
и 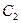 , обращающая это уравнение в тождество по x.
, обращающая это уравнение в тождество по x.
Определение 10. Общее решение, записанное в неявном виде 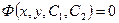 , называется общим интегралом.
, называется общим интегралом.
Определение 11. Частным решением уравнения 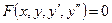 называется решение, полученное из общего решения при фиксированном значении
называется решение, полученное из общего решения при фиксированном значении 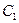 и
и 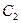 :
: 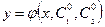 , где
, где 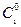 и
и 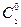 - фиксированные числа.
- фиксированные числа.
Определение 12. Частным интегралом этого уравнения называется интеграл, полученный из общего интеграла при фиксированном значении 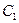 и
и 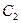 :
: 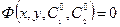 , где
, где 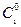 и
и 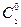 - фиксированные числа.
- фиксированные числа.
Общее решение дифференциального уравнения 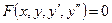 можно рассматривать кА семейство интегральных кривых данного уравнения, зависящее от двух параметров
можно рассматривать кА семейство интегральных кривых данного уравнения, зависящее от двух параметров 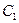 и
и 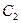 . Частному решению, полученному из общего, соответствует одна кривая этого семейства.
. Частному решению, полученному из общего, соответствует одна кривая этого семейства.
Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти решение, удовлетворяющее начальным условиям 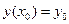 ,
, 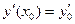 . Постоянные
. Постоянные 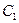 и
и 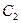 определяются из системы уравнений
определяются из системы уравнений
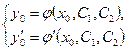
Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить интегральную кривую, проходящую через данную точку 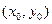 в заданном направлении
в заданном направлении 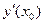 .
.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Определение 13. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида 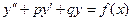 , где
, где 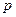 и
и 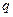 - некоторые числа.
- некоторые числа.
Если 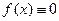 , то дифференциальное уравнение называется линейным однородным. Оно имеет вид
, то дифференциальное уравнение называется линейным однородным. Оно имеет вид 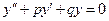 .
.
Справедлива теорема: если 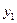 и
и 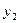 - частые решения уравнения
- частые решения уравнения 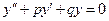 , причем
, причем 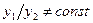 , то функция
, то функция 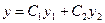 , где
, где 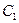 и
и 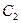 - произвольные постоянные, является общим решением этого уравнения.
- произвольные постоянные, является общим решением этого уравнения.
Решением данного дифференциального уравнения 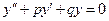 должна быть такая функция, которая, будучи подставлена в уравнение, превратит его в тождество. Левая часть уравнения представляет собой сумму функции y и ее производных
должна быть такая функция, которая, будучи подставлена в уравнение, превратит его в тождество. Левая часть уравнения представляет собой сумму функции y и ее производных 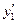 и
и 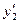 , взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма бранилась в нуль, надо, чтобы y,
, взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма бранилась в нуль, надо, чтобы y, 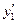 и
и 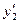 были подобны между собой.
были подобны между собой.
Такой функцией является функция 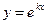 , где
, где 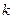 - постоянная. Требуется подобрать
- постоянная. Требуется подобрать 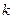 так, чтобы эта функция удовлетворяла уравнению
так, чтобы эта функция удовлетворяла уравнению 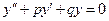 .
.
Так как 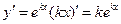 , а
, а 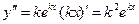 , то, подставляя эти значения y,
, то, подставляя эти значения y, 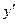 и
и 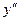 в левую часть уравнения
в левую часть уравнения 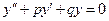 , получим
, получим 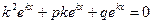 .
.
Сокращая на множитель 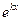 , не обращающийся в нуль, получим характеристическое уравнение
, не обращающийся в нуль, получим характеристическое уравнение 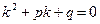 .
.
Это уравнение определяет те значения 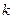 , при которых функция
, при которых функция 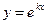 является решением дифференциального уравнения
является решением дифференциального уравнения 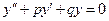 .
.
При решении характеристического уравнения 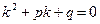 возможны три случая:
возможны три случая:
| № | корни уравнения | частные решения | общее решение |
действительные различные ( 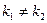 ) ) | 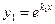 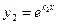 | 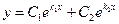 | |
действительные равные ( 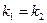 ) ) | 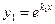 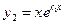 | 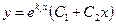 | |
комплексно-сопряженные ( 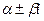 ) ) | 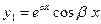 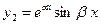 | 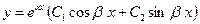 |
Пример 7. Найти общее решение дифференциального уравнения 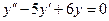 .
.
Решение. Составим характеристическое уравнение и найдем его корни:
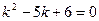 ,
, 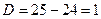 ,
, 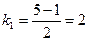 ,
, 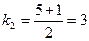 .
.
Корни характеристического уравнения являются действительными и различными. Поэтому 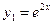 ,
, 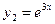 - частные решения, а
- частные решения, а 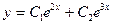 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 8. Найти общее решение дифференциального уравнения 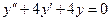 .
.
Решение. Характеристическое уравнение 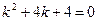 или
или 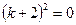 имеет действительные равные корни
имеет действительные равные корни 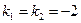 . Поэтому
. Поэтому 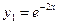 ,
, 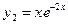 - частные решения, а
- частные решения, а 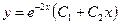 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 9. Найти общее решение дифференциального уравнения 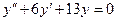 .
.
Решение. Составим характеристическое уравнение и найдем его корни:
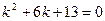 ,
, 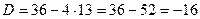 ,
, 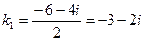 ,
, 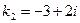 .
.
Корни являются комплексно-сопряженными. Поэтому 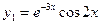 ,
, 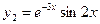 - частные решения, а
- частные решения, а 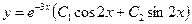 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 10. Найти общее решение дифференциального уравнения 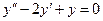 , удовлетворяющее данными начальным условиям при
, удовлетворяющее данными начальным условиям при 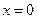 ,
, 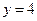 ,
, 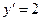 .
.
Решение. Характеристическое уравнение 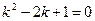 или
или 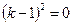 имеет действительные равные корни
имеет действительные равные корни 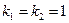 . Поэтому
. Поэтому 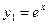 ,
, 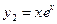 - частные решения, а
- частные решения, а 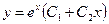 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Для определения частного решения, удовлетворяющего данным начальным условиям, сначала найдем производную 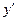 функции
функции 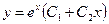 :
:
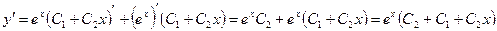 . Теперь подставим начальные условия в выражения для
. Теперь подставим начальные условия в выражения для  и
и 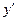 :
:
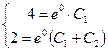
или 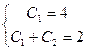 ,
,
откуда 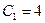 и
и 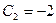 .
.
Подставив эти значения в общее решение, найдем частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям: 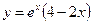 .
.
Упражнения для самопроверки
1. Найдите интегралы:
а) 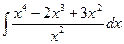 ; б)
; б) 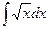 ; в)
; в) 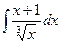 ; г) ;
; г) ; 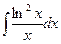 ; д)
; д) 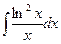 ;е)
;е) 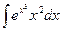 ; ж)
; ж) 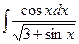 ; з)
; з) 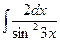 .
.
2. Вычислите определенные интегралы:
а) 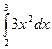 ; б)
; б) 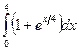 ; в)
; в) 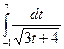 ; г)
; г) 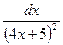 .
.
3. Решите дифференциальные уравнения и найдите частные решения (частные интегралы), удовлетворяющие данным условиям:
а) 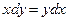 ,
, 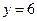 при
при 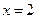 ; б)
; б) 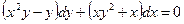 ,
, 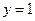 при
при 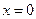 ; в)
; в) 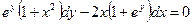 ,
, 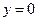 при
при 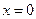 ; г)
; г) 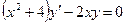 ,
, 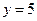 при
при 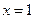 .
.
Ответы: 1. а) 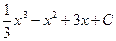 ; б)
; б)  ; в)
; в) 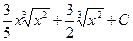 ; г) ;
; г) ; 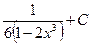 ; д)
; д) 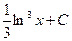 ; е)
; е) 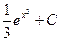 ; ж)
; ж) 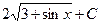 ; з)
; з) 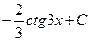 . 2. а) 19; б) 4e; в) 8/3; г) 2/9. 3. а)
. 2. а) 19; б) 4e; в) 8/3; г) 2/9. 3. а) 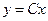 ,
, 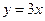 ; б)
; б) 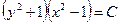 ,
, 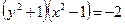 ; в)
; в) 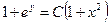 ,
, 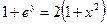 ; г)
; г) 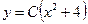 ,
, 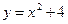 .
.
